EGEE 102
Energy Conservation for Environmental Protection

The Carnot Efficiency

PrintPrint

A general expression for the efficiency of a heat engine can be written as:

Efficiency = Work HeatEnergy Hot MathType@MTEF@5@5@+= feaagGart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqedmvETj2BSbqefm0B1jxALjhiov2DaerbuLwBLnhiov2DGi1B TfMBaebbnrfifHhDYfgasaacH8vrps0lbbf9q8WrFfeuY=Hhbbf9v8 qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9 q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaqaafaaake aacaqGfbGaaeOzaiaabAgacaqGPbGaae4yaiaabMgacaqGLbGaaeOB aiaabogacaqG5bGaaeypamaalaaabaGaae4vaiaab+gacaqGYbGaae 4AaaqaaiaabIeacaqGLbGaaeyyaiaabshacaqGGaGaaeyraiaab6ga caqGLbGaaeOCaiaabEgacaqG5bWaaSbaaSqaaiaadIeacaWGVbGaam iDaaqabaaaaaaa@5325@

We know that all the energy that is put into the engine has to come out either as work or waste heat. So work is equal to Heat at High temperature minus Heat rejected at Low temperature. Therefore, this expression becomes:

Efficiency= Q Hot -Q Cold Q Hot MathTypeMTEF55+= feaagGart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqedmvETj2BSbqefm0B1jxALjhiov2DaerbuLwBLnhiov2DGi1B TfMBaebbnrfifHhDYfgasaacH8vrps0lbbf9q8WrFfeuY=Hhbbf9v8 qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9 q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaqaafaaake aacaqGfbGaaeOzaiaabAgacaqGPbGaae4yaiaabMgacaqGLbGaaeOB aiaabogacaqG5bGaaeypamaalaaabaGaaeyuamaaBaaaleaacaqGib Gaae4BaiaabshaaeqaaOGaaeylaiaabccacaqGrbWaaSbaaSqaaiaa boeacaqGVbGaaeiBaiaabsgaaeqaaaGcbaGaaeyuamaaBaaaleaaca qGibGaae4Baiaabshaaeqaaaaaaaa5040

Where, QHot = Heat input at high temperature and QCold= Heat rejected at low temperature. The symbol (Greek letter eta) is often used for efficiency this expression can be rewritten as:

η ′ ( % )=1− Q Cold Q Hot ×100 MathTypeMTEF55+= feaagGart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqedmvETj2BSbqefm0B1jxALjhiov2DaerbuLwBLnhiov2DGi1B TfMBaebbnrfifHhDYfgasaacH8vrps0lbbf9q8WrFfeuY=Hhbbf9v8 qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9 q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaqaafaaake aacuaH3oaAgaqbamaabmaabaGaaiyjaaGaayjkaiaawMcaaiabg2da 9iaaigdacqGHsisldaWadaqaamaalaaabaGaamyuamaaBaaaleaaca WGdbGaam4BaiaadYgacaWGKbaabeaaaOqaaiaadgfadaWgaaWcbaGa amisaiaad+gacaWG0baabeaaaaaakiaawUfacaGLDbaacqGHxdaTca aIXaGaaGimaiaaicdaaaa4E48

The above equation is multiplied by 100 to express the efficiency as percent.

French Engineer Sadi Carnot showed that the ratio of QHighT to QLowT must be the same as the ratio of temperatures of high temperature heat and the rejected low temperature heat. So this equation, also called Carnot Efficiency, can be simplified as:

η ′ ( % )=1− T Cold T Hot ×100% MathTypeMTEF55+= feaagGart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf MBHbqedmvETj2BSbqefm0B1jxALjhiov2DaerbuLwBLnhiov2DGi1B TfMBaebbnrfifHhDYfgasaacH8vrps0lbbf9q8WrFfeuY=Hhbbf9v8 qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9 q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaqaafaaake aacuaH3oaAgaqbamaabmaabaGaaiyjaaGaayjkaiaawMcaaiabg2da 9iaaigdacqGHsisldaWadaqaamaalaaabaGaamivamaaBaaaleaaca WGdbGaam4BaiaadYgacaWGKbaabeaaaOqaaiaadsfadaWgaaWcbaGa amisaiaad+gacaWG0baabeaaaaaakiaawUfacaGLDbaacqGHxdaTca aIXaGaaGimaiaaicdacaGGLaaaaa4EF7

Note: Unlike the earlier equations, the positions of Tcold and Thot are reversed.

The Carnot Efficiency is the theoretical maximum efficiency one can get when the heat engine is operating between two temperatures:

  • The temperature at which the high temperature reservoir operates ( THot ).
  • The temperature at which the low temperature reservoir operates ( TCold ).

In the case of an automobile, the two temperatures are:

  • The temperature of the combustion gases inside the engine ( THot ).
  • The temperature at which the gases are exhausted from the engine ( TCold ).

It's like taxes. The more money you earn (heat), the more money is taxed (cold), leaving you with less money to take home (efficiency). However, if you could earn more money (heat) and find a way to have less taxes taken out (better engine material), you would have more money to take home (efficiency).

Below is a table showing two temperature scales. The scale labeled "HOT," shows the range of temperatures for the combustion of gases in a car engine. The scale labeled "COLD," shows the range of temperatures at which gases are exhausted from the car engine.

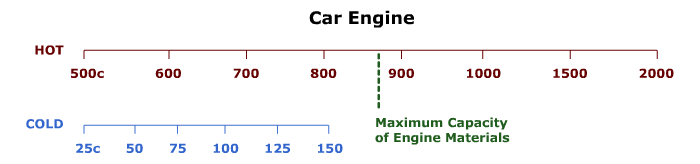
Scales showing car engine combustion temperature ranging from 500 to 2,000 degres C and exhaust gases ranging from 25 to 150 degrees C.
Car Engine Temperatures: red indicates combustion temperatures and blue indicates exhausted temperatures.

Instructions: Look carefully at the efficiency numbers in the body of the table. How do the Hot and Cold temperatures' effect on the efficiency.

Car Engine Efficiency
Hot
500°C		 Hot
600°C		 Hot
700°C		 Hot
800°C		 Hot
900°C		 Hot
1,000°C		 Hot
1,500°C		 Hot
2,000°C
Cold
150°C		 45 52 57 61 64 67 76 81
Cold
125°C		 49 54 59 63 66 69 78 82
Cold
100°C		 52 57 62 65 68 71 79 84
Cold
75°C		 55 60 64 68 70 73 80 85
Cold
50°C		 58 63 67 70 72 75 82 86
Cold
25°C		 61 66 69 72 75 77 83 87

Answer the following questions based on the information in the Car Engine Efficiency table above.

Example

For a coal-fired utility boiler, the temperature of high pressure steam (Thot)would be about 540°C and Tcold, the cooling tower water temperature, would be about 20°C. Calculate the Carnot efficiency of the power plant:

Solution:

Carnot efficiency depends on high temperature and low temperatures between which the heat engine operates. We are given both temperatures. However, the temperatures need to be converted to Kelvin:

T hot = 540 o C+273=813K T cold = 20 o C+273=293​K η=[ 1− T cold T hot ]×100% η=[ 1− 293​K 813​K ]×100% =64%

Practice

For a coal fired utility boiler, the temperature of high pressure steam would be about 540 degrees C and Tcold, the cooling tower water temperature, would be about 20 degrees C. Calculate the Carnot efficiency of the power plant.

Step 1
Convert the high and low temperatures from Celsius to Kelvin:

T hot = 540 o C+273 =813K

T cold = 20 o C+273 =293​K

Step 2

Determine the efficiency using the Carnot efficiency formula:

η=[ 1− T cold T hot ]×100% η=[ 1− 293​K 813​K ]×100% =64%
From the Carnot Efficiency formula, it can be inferred that a maximum of 64% of the fuel energy can go to generation. To make the Carnot efficiency as high as possible, either Thot should be increased or Tcold (temperature of heat rejection) should be decreased.

Practice Problem

Use the following link to generate a random practice problem.