The following examples can help you better understand escalated and constant dollar analysis.
Example 5-1:
Calculate the ROR for the investment that includes 1,000 and 1,200 dollar costs at the present time and at the end of the first year, which yields 800, 1,200, and 1,600 dollars of income at the end of the second, third, and fourth years. There is no salvage value.
Cash flow for this investment can be shown as:
| C0=$1,000 | C1=$1,200 | I2=$800 | I3=$1,200 | I4=$1,600 |
|
|
||||
| 0 | 1 | 2 | 3 | 4 |
By the trial and error method or with the IRR formula in Microsoft Excel, ROR for this project is calculated as: i=20.5%.
Figure 5-1 shows how this problem can be formulated in Microsoft Excel.
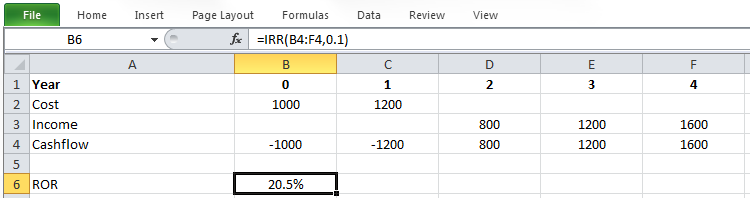
Escalated Dollar Analysis
Example 5-2:
Now assume for the above investment, costs and incomes will be escalated with the rate of 18% and 12% per year. Calculate the escalated dollar ROR for this investment.
For the escalated method, we need to utilize single payment compound amount factors (F/Pi,n) to convert (compound) the today’s dollar value to escalated dollar regarding the escalation rate:
| C0=$1,000 | C1=$1,200*(F/P18%,1) =1,416 |
I2=$800*(F/P12%,2) =1,003.52 |
I3=$1,200*(F/P12%,3) =1,685.91 |
I4=$1,600*(F/P12%,4) =2,517.63 |
|
|
||||
| 0 | 1 | 2 | 3 | 4 |
Note that escalation has no effect on the cost in the present time (1,000 dollars) because it assumes that all the amounts happen at the end of the year.
The rest of the solution for determining ROR is similar to before:
And ROR for this project is calculated as: i=33.6%. Figure 5-2 displays the way this problem can be formulated in Microsoft Excel..
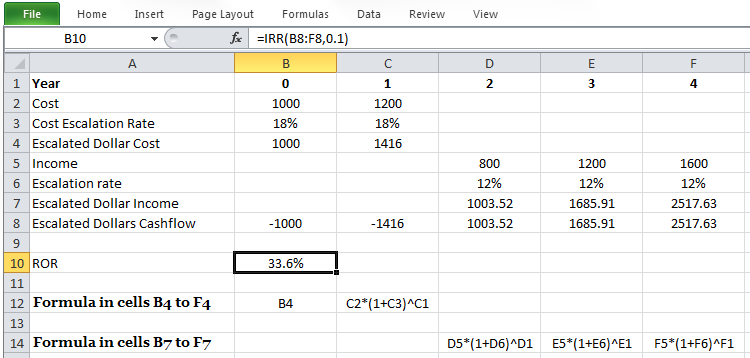
Constant Dollar Analysis
Example 5-3:
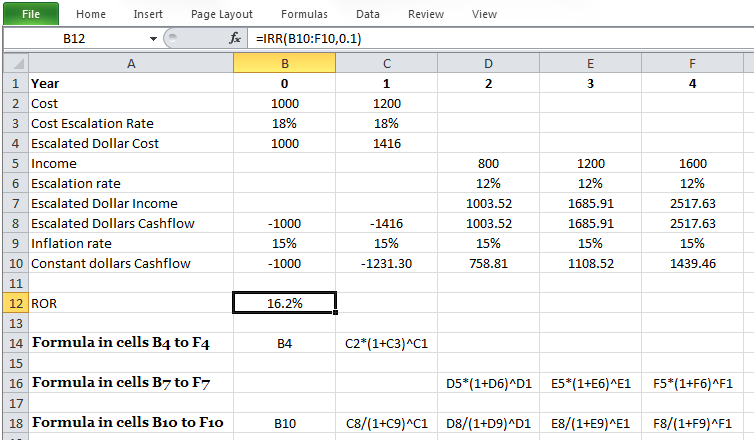
Now, determine the constant dollar ROR for the investment explained in Example 5-2 assuming an annual inflation rate of 15%.
In order to remove the effect of the inflation rate from our calculations, we need to discount the escalated dollars from previous analysis at the rate of inflation to express all dollar values in terms of time zero purchasing power. It can be done using the single payment present worth factor (P/Fi,n) with the assumed inflation rate.
| C0=$1,000 | C1=$1,416*(P/F15%,1) =1,231.30 |
I2=$1,003.52*(P/F15%,2) = 758.81 |
I3=$1,685.91*(P/F15%,3) = 1,108.52 |
I4=$2,517.63*(P/F15%,4) = 1,439.46 |
|
|
||||
| 0 | 1 | 2 | 3 | 4 |
Here, $1,231.30 at year 0 would purchase the goods and service that $1,416 would purchase at year 1, if inflation is 15% per year. $758.81 at year 0 would purchase the goods and services that $1,003.52 would purchase at year 2 if inflation is 15% per year and so on. The rest of the calculations are similar to before:
Where i' equals constant dollar ROR. And i'= 16.2% is calculated as ROR for constant dollar.
The following figure displays how constant dollar analysis can be formulated in Microsoft Excel.
Please watch the following video (6:28): Escalated and constant dollar rate of return analysis.
PRESENTER: Let's work on an example to calculate the rate of return for escalated dollar cash flow and also constant dollar cash flow. This cash flow is given for an investment. So let's calculate the rate of return. In order to calculate the rate of return, we'd write the equation,the present value of costs equals the present value of income plus the present value of salvage. We don't have salvage value here. So the present value of costs equals the present value of income. We have two costs here-- $1,000 at present time and $1,200 at year one. And we're going to have three incomes of $800, $1,200, and $1,600 in a year two, three, and four.
So we write the equation and solve it for I and calculate the rate of return as 20.5%. Now let's consider an escalation rate of 18% for costs and escalation rate of 12% for income. Let's calculate the escalated dollar cash flow and then we will calculate the rate of return for the escalated dollar cash flow. In order to calculate the escalated dollar cash flow, we need to compound each payment by the escalation rate and considering the compound periods.
The payment at year 0 is not going to be affected by the escalation. So it stays unchanged. The cost of $1,200 at year 1 will be compounded with an 18% escalation rate because this is a cost and the compounding period will be 1. The income of $800 at year 2 will be escalated with 12% because this is an income and the compounding period will be two years and so on-- the income of $1,200 at year three, 12% escalation rate and three years compounding period and $1,600 income, 12% escalation rate and 4 compounding period-- and the result.
So we are going to have escalated cash flow at this cash flow that we can see here. And we want to calculate the rate of return for this escalated dollar cash flow. Again, we write the equation, the present value of cost equals the present value of all income. We have 2 costs here-- $1,000 and $1,416, which are escalating dollar cash flow. So if we write the equation, the present value of costs equals the present value of income, we have three incomes here-- the income at year 2, income at year 3, and income at year 4.
And we solve this equation for I. And we calculate that escalated dollar rate of return as 33.6%. So we calculated our escalated cash flow as the cash that you can see here. Now let's consider the inflation rate of 15%, and let's calculate the constant dollar cash flow and then calculate the rate of return for the constant dollar cash flow.
In order to remove the effect of the inflation rate from our calculations, from our escalated dollar cash flow, we need to discount each payment in the escalated cash flow by the inflation rate and considering the discounting period. So we need to multiply each payment and the escalated cash flow by the single payment present worth factor or factor p over f, considering the inflation rate and the discounting period to calculate the constant dollar cash flow. So as you can see here, we discount each payment by the inflation rate, which was 15%, and the discounting period.
You know that the present time is not going to be affected by the inflation rate. So we start from year 1, the escalated dollar cash flow. We multiply it by the single payment prison worth factor. This 15% is the inflation rate. And 1 is the discounting period. For year 2, the same inflation rates. The discounted period is going to be 2, and so on for year 3 and year 4.
And we calculate the result, which shows the constant dollar cash flow. So it means, for example, $1,231 at year 0 would have the same purchasing power as $1,416 in year 1. And let's calculate the rate of return for these constant dollar cash flow. Again, the equation is the present value of cost equals the present value of income. We have two constant-dollar costs and three incomes. So if we write the equation and we solve it for I and we calculate that the constant dollar rate of return as 16.2%. So we show it with I prime. And it is the constant dollar rate of return.
After calculating the ROR for the project, in order to complete the assessment and make the proper decision, it is necessary to compare it with the minimum rate of return (that is determined by other investment opportunities) to see if the project is economically satisfactory. To do so, you should be very careful using the proper minimum rate of return that is reported in escalated or constant dollars. For example, if other investment opportunities give 25% ROR on escalated dollars (it means the minimum rate of return on escalated dollars is 25%), we can conclude that this project with ROR of 33.6% is economically satisfactory. But the minimum rate of return of 25% on escalated dollars can’t be compared with the calculated 16.2% constant dollar.
As you can see in Example 5-2 and 5-3 for ROR calculations, P/Fi,n and P/Ff,n * P/Fi’,nsub> are similar:
i: escalated dollar ROR
i': constant dollar ROR
f: inflation rate
This mathematical proof is known as the “Fisher Rule.” This equation is a simpler way for calculating constant dollar ROR given the inflation rate and escalated dollar ROR. For example, i= 33.6% was calculated in Example 5-2 as ROR for escalated dollar analysis. In Example 5-3, ROR for a constant dollar is asked for the inflation rate of 15%. According to Equation 5-1, equals constant dollar ROR can be determined:
Which is equal to the Example 5-3 results.
Equation 5-1 can also be utilized to determine the minimum rate of return for constant dollars knowing the inflation rate and minimum rate of return for escalated dollars. In this case, i should be replaced with i* and i' with i'*:
i*: escalated dollar minimum rate of return
i'*: constant dollar minimum rate of return
f: inflation rate
For example, if the minimum rate of return (for other investment opportunities) for escalated dollars is considered 25%, the minimum rate of return for constant dollar assuming an inflation rate of 15% can be calculated as:
Please watch the following video (6:41): The Fisher Rule.
PRESENTER: In this video, I'm going to explain how to use the Fisher Rule to convert the escalated dollar and constant dollar rates. So, in the previous example, we calculated the rate of return for the escalated dollar cash flow and also for the constant dollar cash flow. But after we calculate the rate of return, we need to compare it with something with a minimum rate of return to conclude that if we're going to have a good investment or not, if the project is going to be economically satisfactory or this is not going to be a good project.
Here is a summary of the previous example's results. So this is the escalated dollar cash flow. And the rate of return for escalated dollar cash flow is 33.6%. And this is the constant dollar cash flow that we calculated. And the rate of return for constant dollar cash flow was 16.2.
So we have two rates of returns, the escalated dollar cash flow rate of return and constant dollar cash flow rate of return. So, for example, if we have other investment opportunities that give a 25% rate of return on the escalated dollar cash flow, then we can conclude that this is a good investment because the escalated dollar cash flow is 33.6% and we can conclude that this project is economically satisfactory. But the minimum rate of return of 25% on the escalated dollar cannot be applied to the constant dollar rate of return. This is a very important point that you should always be very careful about.
So as you saw in previous slides, escalated dollar rates cannot be compared with the constant dollar rates. So the Fisher Rule is the equation that helps us compare and convert these rates. I wrote the equation here. I is the escalated dollar rate of return. I prime is the constant dollar rate of return and f is the inflation rate.
So you can calculate any of these from the other two. And this is applicable for any other rates. So here its for the rate of return. But you can use this equation for any other rates that you need to convert for the escalated dollar or the constant dollar.
So using this equation, we can simply calculate the constant dollar rate of return given the inflation rate and escalated dollar rate of return. So we can calculate any rate, any constant dollar rate, given the inflation rates and constant dollar rate.
So, for example, we calculated the escalated dollar rate of return as 33.6% and we considered the 15% of inflation rate. Knowing these two, using the Fisher Rule, we can easily calculate the constant dollar rate of return. So we just plug the i and f escalated dollar rates and inflation rate and we calculate the i prime or the rates, the constant dollar rate, as 16.2, which is exactly the same as what we calculated for the constant dollar rate of return.
So again, Fisher Rule can be used to convert any escalated dollar rate to the constant dollar rate using the inflation rate. For example, using the Fisher Rule, we can calculate the minimum rate of return for the constant dollar given the inflation rate and the minimum rate of return for the escalated dollars. So we'll rewrite the equation as the equation 5-2. I star is an escalated dollar minimum rate of return. I prime star is the constant dollar minimum rate of return. And f is the inflation rate.
So going back to the previous example, the escalated dollar minimum rate of return was considered as 25%. So if we want to calculate the minimum rate of return for constant dollar, we can use the Fisher Rule and consider the inflation rate of 15% and calculate the minimum rate of return for the constant dollar as 8.6%. Please remember we calculated the escalated dollar cash flow as 33.6%. And the minimum rate of return for the escalated dollar cash flow is 25%. And then we concluded that, because the rate of return is higher than the minimum rate of return, this project is economically satisfactory.
But we said that you cannot compare the constant dollar cash flow rate of return with this 25%. So we need to calculate. We needed to calculate the minimum rate of return for constant dollar cash flow. And that's what we calculated as 8.7%.
So because the 16.2% rate of return for the constant dollar cash flow is higher than 8.7% of the minimum rate of return for the constant dollar cash flow, we can conclude that this project is economically satisfactory. So our new base to compare the constant dollar cash flow is the constant dollar minimum rate of return of 8.6%