This section provides more examples of how to evaluate the economic potential of an investment project based on ROR and NPV analysis. In the following example, the escalated dollar minimum ROR is assumed 15%, and the inflation rate will be 6%. As previously explained, Equation 5-2 can be applied to calculate the constant dollar minimum rate of return.
Example 5-4:
Calculate ROR for the investment that has the following projected today’s dollar costs and revenue:
| C0=$50,000 | C1=$80,000 |
Rev2=$100,000
OC2=30,000 |
Rev3=$90,000
OC3=30,000 |
Rev4=$80,000
OC4=30,000 |
L=0 |
|
|
|||||
| 0 | 1 | 2 | 3 | 4 | |
C: Capital Cost, OC: Operating Cost, Rev: Revenue, L: Salvage
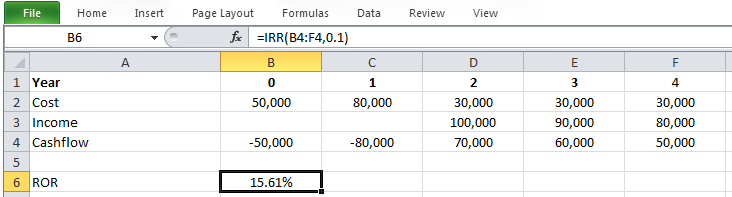
So, ROR can be calculated as i = 15.61%.
Example 5-5:
Now, assume escalation rates of 8% per year for capital cost (development cost), 12% per year for operating costs and 10% per year for revenues. Calculate ROR and NPV for this investment, and make escalated dollar analysis considering 15% escalated dollar minimum rate of return, i*.
| C0=$50,000 | C1=$80,000*(F/P8%,1) =86,400 |
Rev2=$100,000*(F/P10%,2) =121,000 OC2=30,000*(F/P12%,2) =37,632 |
Rev3=$90,000*(F/P10%,3) =119,790 OC3=30,000*(F/P12%,3) =42,148 |
Rev4=$80,000*(F/P10%,4) =117,128 OC4=30,000*(F/P12%,4) =47,206 |
|
|
||||
| 0 | 1 | 2 | 3 | 4 |
Present value of all costs = present value of all revenues
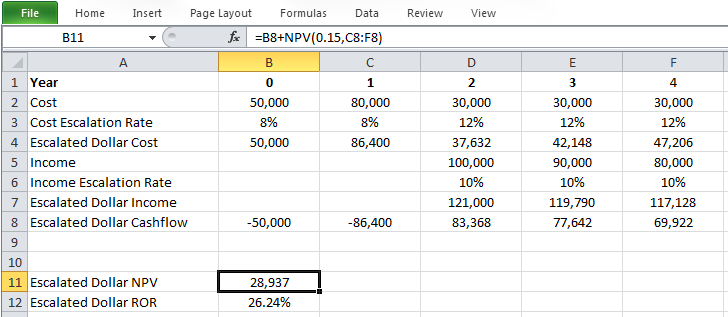
Escalated dollar ROR for this project is calculated as: i=26.24%, and it is higher than 15% escalated dollar minimum rate of return, i*. So, the project is economically satisfactory.
Since NPV at 15% escalated dollar minimum rate of return is positive, we can conclude that the project is economically satisfactory.
Example 5-6:
Now, consider inflation rate of 6% per year for Example 5-5 and make constant dollar analysis.
Constant dollar amounts can be calculated as:
| C0=$50,000 | C1=$86,400*(P/F6%,1) = 81,509.43 |
Rev2=$83,368*(P/F6%,2) = 74,197.22 |
Rev3=$77,642*(P/F6%,3) = 65,189.85 |
Rev4=$69,922*(P/F6%,4) = 55,385.11 |
|
|
||||
| 0 | 1 | 2 | 3 | 4 |
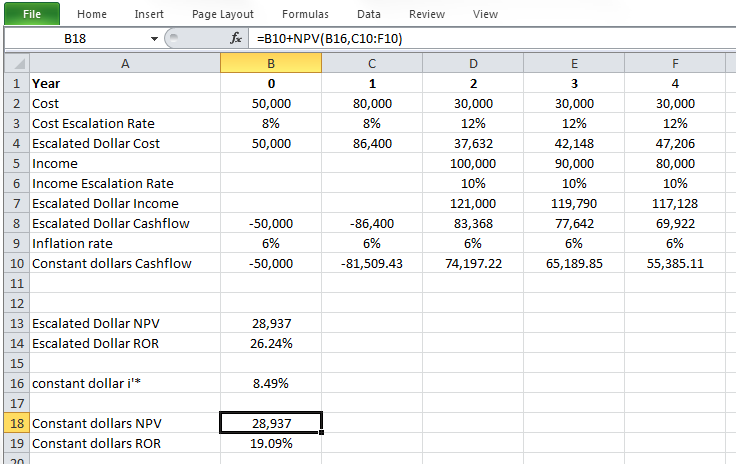
ROR for this project is i=19.09%,
For constant dollar analysis, it is necessary to derive constant dollar minimum rate of return, i'*, from escalated dollar minimum rate of return, i*, and inflation rate applying equation 5-2.
Therefore, the constant dollar minimum rate of return, i'*, will be 8.49%.
The constant dollar ROR for this project is calculated as 19.09%, and it is higher than i'* = 8.49%. So, the project is economically satisfactory.
In order to calculate the constant dollar NPV, we have to calculate it at a constant dollar minimum rate of return, i'*= 8.49%.
Constant dollar NPV at i'*= 8.49% is positive, so, the project is economically satisfactory.
Please watch the following (17:17) video: Escalated and constant dollar ROR and NPV analysis
PRESENTER: Now let's work on a more comprehensive example. And I'm going to use an Excel spreadsheet to work on this example. And this is the data for an investment.
We are going to have investments of $50,000 and $80,000 at the present time and Year 1. We are going to have the revenues of $100,000, $90,000, and $80,000 at Year 2, 3, and 4. And the operating cost is going to be constant at $30,000 from Year 2 to Year 4.
We are going to consider the escalation rate of 8% for the capital cost and 12% for operating costs and 10% of escalation for the revenues. Let's calculate the rate of return and NPV for this investment and calculate the escalated dollar cash flow.
So because we have different escalation rates for our costs and revenue, we need to separate-- we need to keep them separate. The present time capital cost will not be affected by the escalation rate. The $80,000 of capital cost at Year 1 has to be compounded with 8%. And the compounding period is 1.
The $100 revenue at Year 2 has to be compounded by 10%, and the compounding period is 2. The operating cost at Year 2 has to be compounded by 12%, and the compounding period is 2, and so on. Payments are going to be 3 and the compounding period is going to be 4 years. The escalation rate for revenue is 10%, and the escalation rate for operating costs is 12%.
And the result.
So in order to calculate the rate of return, we write the equation for the rate of return, the present value of cost equals the present value of revenue. The present value of costs equals the present value of all capital costs and operating costs that we have here. And the present value of income equals the present value of revenue at Year 2, 3, and 4.
We could also make a summation over each column, considering the negative sign for costs, and calculate the escalated dollar cash flow and write the rate of return equation for that. Both of them are the same. And we solved the equation for i.
And we calculate the rate of return, the escalated dollar cash flow rate of return as 26.24%. So because the calculated rate of return for this project is higher than 15% escalated dollar minimum rate of return, we can conclude that this project is economically satisfactory.
So we can also calculate the NPV for this project. NPV equals the present value of all costs, considering the 15% of escalated dollar minimum rate of return, considering the negative sign, plus the present value of revenue, considering 15% of escalated dollar minimum rate of return. So we calculate the NPV as $28,937. So because this NPV is positive, we can conclude that this project is economically satisfactory.
So let me open the Excel spreadsheet and work on this example. So this is the information for this investment. These are costs. The first two ones are capital costs and the other three are operating costs. As you can see, escalation rates are different. And here, the income.
So now I'm going to calculate the escalated dollar. So for the payment, which is the capital cost at the present time, which will not be affected by the escalation rate, so it is going to be the same payment. Escalated dollar cost at Year 1 can be calculated by compounding this $80,000 by 8% and for 1 year compounding period, so it equals $80,000, multiply 1 plus 8% power 1. So this is the escalated dollar cost at Year 1.
And I can apply to the other cells. For example, the last year, which is going to be an operating cost, has to be compounded by 12% of the escalation rate and 4 compounding periods. F1, which reads it from here.
And then I'm going to calculate the escalated dollar income for our trade incomes in Year 2 to Year 4. So escalated dollar income of $100,000 equals $100,000, multiply 1 plus 10% power 2, because we are going to have two compounding periods. And I apply that to the other revenues.
And now I'm going to calculate the escalated dollar cash flow, which is going to be revenue, the escalated dollar income revenue, minus the escalated dollar cost. I don't have any revenue at the present time, so it will be 0, but I have to write that, minus the costs. And I apply this to the other years.
So this is going to be my escalated dollar cash flow. I am going to calculate the escalated dollar NPV. Because I have a payment at the present time, I have to enter that manually and then use the NPV function for the rest.
The rate was 15%. And then I will choose the cash flow, the rest of the cash flow. So this is escalated dollar NPV and the rate of return. I used the IRR function.
I choose the entire cash flow. And I enter a guess, which I just gave at 10%. And 26.24% is the escalated dollar rate of return.
So this is the escalated dollar cash flow that we just calculated. Now let's consider an inflation rate of 6% per year for this escalated dollar cash flow. And let's calculate the constant dollar cash flow. And then, let's calculate the rate of return and NPV for constant dollar cash flow.
In order to calculate the constant dollar cash flow, we need to discount each payment by the inflation rate, a 6% inflation rate, considering the discounting period. For example, the escalated dollar of $86,400 at Year 1 has to be discounted by 6%, and the discounting period, which is going to be 1, and so on. For Year 2, the discounting period is 2, 6% inflation rate, and so on. And the results.
So this is going to be our constant dollar cash flow. We write the rate of return equation. And we solve the equation for i. And we calculate the constant dollar rate of return as 19.09%.
Now let's calculate the NPV for constant dollar cash flow. But a very important thing here is what rate should be used to calculate the NPV for constant dollar cash flow? We know that the escalated dollar minimum rate of return is 15%. But we cannot use the escalated dollar minimum rate of return for constant dollar NPV calculations.
So what should we do here? We can use the Fisher equation to convert the escalated dollar minimum rate of return into the constant dollar minimum rate of return using the inflation rate. So here is the Fisher equation.
This 15% is an escalated dollar minimum rate of return and a 6% interest rate. The result is going to be 8.49%, which is going to be the constant dollar minimum rate of return. This is the rate that we have to use for calculating our constant dollar NPV.
So we use the constant dollar minimum rate of return of 8.49% to calculate the NPV of constant dollar cash flow. And this is the NPV of constant dollar cash flow. And you can see because this is positive, we can conclude the project is economically satisfactory.
We calculated the constant dollar rate of return as 19.09%. And we need to compare this with the constant dollar minimum rate of return of 8.49% that we just calculated. And because this rate of return is higher than this minimum rate of return, we can also conclude that this project is economically satisfactory.
Now let me open the Excel spreadsheet again. So this is the escalated dollar cash flow. And we are going to consider the 6% of inflation rate for this escalated dollar cash flow. And then we have to calculate the constant dollar cash flow.
In order to calculate the constant dollar cash flow, we need to discount each payment by 6% and the discounting period. So we can leave it as it is, $50,000 of costs. But this escalated dollar cash flow has to be discounted by 1 plus 6%, our discounting period. And then I can apply this to the other years. So for example, the last year, constant dollar cash flow in the last year equals the escalated dollar divided by 1 plus inflation rate power the year.
Now let's calculate the constant dollar NPV. But in order to calculate the constant dollar NPV, we need the constant dollar minimum rate of return. How do we calculate that? I will use the Fisher equation, escalated dollar minimum rate of return, and the inflation rate to calculate the constant dollar minimum rate of return.
So constant dollar minimum rate of return, or i prime star, equals 1 plus 15%, which was escalated dollar minimum rate of return, divided by 1 plus inflation rate, 6%, minus 1, which equals 8.49%. So this 8.49% is the constant dollar minimum rate of return that I can use to calculate the constant dollar NPV.
So I have the constant dollar cash flow here. I have a constant dollar minimum rate of return here. And I can calculate the constant dollar NPV.
So the payment at the present time, I have to enter that manually, plus the NPV function. The rate is a constant dollar minimum rate of return and the rest of the constant dollar cash flow. So because this NPV is positive, I can conclude that the constant dollar cash flow of the project with this constant-dollar cash flow is a good project to invest.
And let's calculate the constant dollar rate of return, which is a fairly straightforward, IRR function. I choose the constant dollar cash flow. I give it a guess, 10%. And this is the constant dollar rate of return, which is 19.09%. And because this constant-dollar rate of return is higher than the constant dollar minimum rate of return, I can conclude that this project is economically satisfactory in terms of rate of return.
So you can also use the Fisher rule to calculate the constant dollar rate of return. Keep it in your mind. It's a very good double-check method to make sure your final result is correct.
So we have the constant-- we have the escalated dollar rate of return here. We have an inflation rate of 6%. So with these two, I should be able to calculate the constant dollar rate of return using the Fisher rule.
So let's see. So the constant-dollar rate of return using the Fisher equation is 1 plus escalated dollar rate of return divided by 1 plus inflation rate of 6% minus 1. And it should give me the exact same value as this rate of return that I calculated here. As you can see, it will be the same.
Summary of calculations:
- Step 1: Calculating escalated dollar cash flow using escalation rate and F/P factor
- Calculating escalated dollar ROR from calculated escalated dollar cash flow in step 1
- Calculating escalated dollar NPV from calculated escalated dollar cash flow in step 1 and given escalated dollar minimum rate of return, i*
- Step 2: Calculating constant dollar cash flow using the given inflation rate and P/F factor from the calculated escalated dollar cash flow in step 1
- Calculating constant dollar ROR from calculated constant dollar cash flow in step 2
- Calculating constant dollar minimum rate of return, i'*, from given escalated dollar minimum rate of return, i*, and given inflation rate, f, using Fisher equation
- Calculating constant dollar NPV from calculated constant dollar cash flow in step 2 and calculated constant dollar minimum rate of return, i'*
Note that the constant dollar NPV is identical to the escalated dollar NPV. Constant NPV equations are mathematically equivalent to escalated dollar NPV equations and then give the same results.
Note that Example 5-4 implicitly assumes the escalation rate is 0% per year. So, for NPV and ROR analysis in Example 5-4, we need to consider a 15% escalated dollar minimum rate of return.
And since it is positive, the project is economically satisfactory.
And calculated ROR (15.61%) is also higher than the 15% escalated dollar minimum rate of return, so we can conclude that the project is economically satisfactory.