One of the key economic impacts expected from the solar heat applications is fuel deduction costs. While deploying solar collectors involves additional up-front capital costs, the operational costs are much lower compared to fuel-fired units. However, due to reliability requirements, auxiliary energy supply is still typically included in industrial applications. In this case, the useful energy from the solar system is used to reduce the auxiliary fuel consumption.
Solar thermal systems are relatively high in capital costs compared against alternative thermal energy systems. However, the solar fuel is free. As such, the cost structure is inherently different from low capital cost but relatively high and often volatile fuel costs associated with petroleum, coal, natural gas, and other fossil fuel thermal energy systems. So another attractive aspect of solar thermal systems, and one of the primary drivers behind their growing installations worldwide, is the insulation that such systems provide against price shocks of fossil fuels.
For industry, taking into account depreciation rates over the long-term projects is important. In this connection, discounted cash flow analysis is a good tool to estimate the Net Present Value (NPV) of the project and realistic pay-back time. Those metrics are initially used to evaluate the economic viability of the project.
Let us recall what Net Present Value (NPV) is. In brief, NPV is the current value - as of today - of all related cash flows through the time of the project. Because $100 today is worth more than $100 next year (due to inflation rate), expenditures that will occur in the future are not valued as much as the same expenditures occurring today. This is why cheap natural gas boilers often appear as an economic choice in the light of the high capital cost of a solar thermal energy systems. Below we review the basic methods of calculating NPV.
Simple payback approach
This approach is suitable for short-term projects with quick return on investment. In this case, discounting (for money value declining over time) may be unnecessary.
In simple payback evaluation, all cash flows into and out of the project are added up to find Net Present Value (NPV). That includes initial cost (capital investment), annuities (net utlility obtained from the operation, i.e. renevue minus maintenance and operation costs), and salvage value (in the end of the project) (Vanek and Albright, 2008):
NPV = Initial Cost + S(Annuities) + Salvage Value
- If NPV is positive, the project is considered financially viable.
For example, consider a hypothetical technology project with the initial cost of $100,000, net positive annuity of $20,000 for 10 years, and a salvage value in the end of that term of $5,000. Then, its net present value can be calculated as:
NPV = - 100,000 + (10 years x 20,000) + 5,000 = $105,000
The positive NPV value indicates that the project is financially viable.
The break-even point, i.e., the year when the sum of annuities surpasses the initial cost, and the initial expenditures have been paid back, is characterized by the Simple Payback Period (SPB):
SPB (years) = Initial Cost / Net annuity
- SPB indicates the number of years after which the initial expenditures are paid back.
For the case described above:
SPB = $100,000 / $20,000 = 5 years
Capital Recovery Factor (CRF) evaluates the relationship between the cash flow and investment cost. This evaluation is applicable to short-term investments (within N=10 years).
CRF = ACC / NPV
where ACC = Annual Capital Cost
ACC = Annuity – NPV/N
Here, the NPV/N term is the average share of the net present value per each year of the project. So, ACC is the part of the annuity that goes each year to cover the investment; it does not go towards profit.
For the hypothetical project example described above, we can calculate:
ACC = $20,000 – $105,000/10 = $9,500
CRF = $9,500 /$105,000 = 0.09 (9%)
- CRF factor should not be too high for a project to be considered financially viable.
By recommendation of the Electric Power Research Institute (EPRI), CRF value should not exceed 12%.
Discounted Cash Flow Analysis
This approach is better applied to long-term projects with slow payback. Money value declines over time, so it must be taken into account. This is especially relevant to solar projects, which typically have high capital costs and long pay-pack periods.
In the case of discounted cash flow, we need to evaluate how much any cash flow element would value in the future. That would depend on the interest rate (i) imposed on initial investment and the number of years (N) the project is underway. The following conversion factors are used to adjust the future money values (Vanek and Albright 2008):
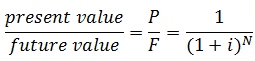
and
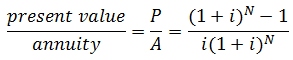
Then the discounted flow NPV can be derived as follows:
NPVfuture = Initial cost + (P/A) × Annuity + (P/F) × Salvage value
For the example used in simple payback approach section above, if the interest rate on the initial investment is set at 5%, the conversion factors for 10-year project can be calculated as:
(P/F, 5%, 10) = 0.614 and (P/A, 5%, 10) = 7.722
And the discounted NPV future value can be found as:
NPVfuture = Initial cost + (P/A) × Annuity + (P/F) × Salvage value =
= -100,000 + 7.722 × 20,000 + 0.614 × 5,000 = $57,510
Here, when depreciation is taken into account, the NPV value is much lower than that in case of simple payback assessment. But the NPV of this project is still positive, indicating that the project is economically viable.
Supplemental Reading:
Vanek, F.M. and Albright, L.D., Energy Systems Engineering, McGraw Hill, 2008. Chapter 3. Economic Tools for Energy Systems.
In case of solar system providing heating for a facility or a process, the generated thermal energy is not sold to create monetary revenue, but instead is accounted in energy savings. So amount money saved per year can be assigned as monetized benefit.
Example
Let us estimate the NPV values for a hypothetical solar collector system of total area 10 m2 designed to offset the thermal energy expenditures of a building. Assume the system cost estimated at $725 per m2 of collector surface. This includes cost of collector, associated storage, pumps, and piping. Also assume that the yearly energy savings from the solar system are 7500 kWh, and the monetary value of energy is $0.16 per kWh (this is how much the consumer would need to pay for electric water heating if the solar system is not employed). Would this system be viable over the term of 15 years? or 10 years?
Based on these parameters and assumptions, the total system installation cost will be $725/m2 x 10 m2 = $7250. We can neglect possible maintenance or repair costs in this example. So this will be the total investment.
Then, the monetary value of the saved energy will be: 0.16 $/kWh x 7500 kWh/year = $1200. This is how much annuity (in terms of energy saving) the system brings.
To assess the economic viability, first we can use the simple payback check:
NPV = - 7250 + (1200 x 15) = $10,750
This is a positive value, therefore the project makes economic sense. However, depreciation rate is not taken into account here. If we assume that depreciation is 5% (and this is how much interest will be put annually on the initial investment), we can estimate the discounted NPV as follows:
NPVfuture = Initial cost + (P/A) × Annuity + (P/F) × Salvage value
where the (P/A, 5%, 15) factor is equal to 10.38 (if you apply the above-mentioned formula). The (P/F) factor is not needed in this calculation because we are not considering any salvage value. So finally:
NPVfuture = - 7250 + (10.38 x 1200) = $5,206
This is again a positive value, so with the current economic conditions, the project is considered viable.
Self-check
Now perform the same NPV calculation for a 10-year term and a 5-year term. What do these results tell us?
Simple payback: NPV = $4,750
Discounted: NPV = $2,016
Although the value is positive, it is much lower now than in 15-year case. Is it positive enough?
As an additional step, we can check CRF value. In this case it comes to 15% which is too high to make the investment financially attractive.
Simple payback: NPV = -$1,250
Discounted: NPV = -$2,055
With negative NPV values, this project is not considered viable over 5-year term.
Another thing to consider in the economics of the solar heat - industrial process combo is investment tax credits. Those incentives effectively reduce the up-front capital costs and may create a more favorable economic scenario and allow solar to compete with relatively cheap fossil fuel heat generation. So if available in specific location, tax credits should be included in the cash flow analysis.
