Hydropower
Like moving air, moving water has kinetic energy (it has mass and it is moving). But water is much denser than air - this is obvious to anyone who has waded across a deep stream or played in ocean waves. If you recall, air has an average density of 1.225 kg/m3. One cubic meter of water, on the other hand, has a mass of 1,000 kg, or one metric ton (aka one tonne). It may be hard to believe, but a cube of water that is about 3.3 feet on each side weighs over 2,000 pounds!
Where does this kinetic energy come from? Take a second to think about it...Water only flows downhill, so if you see moving water it came from a higher elevation. This kinetic energy is thus converted from gravitational potential energy. How did it get this gravitational potential energy? Well, something had to take the water up to the higher elevation. The only natural way this happens is through evaporation, which is almost always caused by the sun, in a number of different ways: Water that is heated by the sun may evaporate. Wind also evaporates water, but remember that wind gets its energy from the sun. Plants evapotranspirate water, but again, they get their energy from the sun. Even the minor amount exhaled by humans is solar energy since all of our energy comes from the sun. The only major exception is that some evaporative heat is provided by geothermal energy from the earth, e.g., in volcanoes. At any rate, almost all hydropower/energy comes from the sun
How a Hydropower Plant Works
Humans have been using hydropower for thousands of years. According to the U.S. Department of Energy, the Greeks used water to spin wheels to grind grain over 2,000 years ago. Modern humans figured out how to convert hydropower to electricity by using a turbine and generator (see below), which is called hydroelectricity, for obvious reasons. The first known use of hydroelectricity was in 1878 to power a single lamp in Northumberland, England. Larger plants were installed in 1881 in the U.S., and the first commercial-scale plant was built in the U.S. in 1893 in Redlands, California.
All hydroelectric power plants operate on the same principle. Moving water spins a turbine, which spins an electric generator. See below for an illustration of an impoundment facility, which uses a dam to create a reservoir of water.
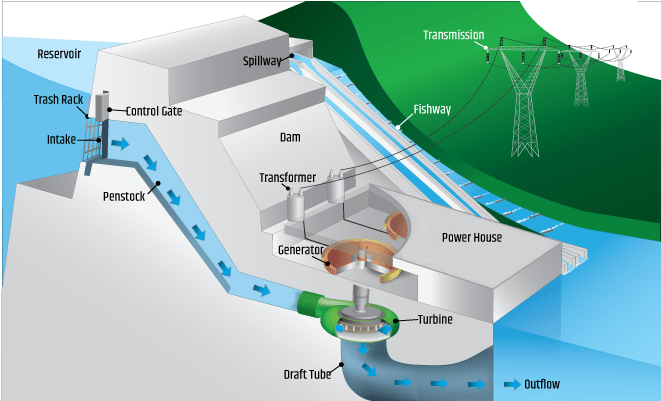
Explaining all components in this image goes beyond the scope of this lesson. The important terms for this lesson are:
- The penstock is a conduit through which the water flows from a higher to a lower elevation.
- The turbine spins due to the force of the water flowing out of the penstock.
- The turbine spins the generator, which generates electricity.
This basic process - flowing water spins a turbine, which spins a generator - is common to all types of hydroelectricity installations. There can be any number of other components, and the size/scale may be different, but this core process is the same.
Microhydroelectricity
Like all other electricity sources, hydroelectric power plants have a rated capacity. Large impoundment facilities can have capacities on the order of GWs (billions of watts). The largest facility in the world - the Three Gorges Dam in China - has a capacity of 18 GW. According to the U.S. Department of Energy, a microhydro system has a capacity of up to 100 kW. Most systems are much smaller. A residential-scale microhydro system is more likely to be a few kWs in size.
A typical microhydro system is illustrated in the image above. Systems can vary significantly in style and size, but according to the U.S. DOE, the following components are commonly seen in most systems:
- The water is often diverted from a stream. If so, it is usually transported to a forebay, which is akin to a small impoundment facility that creates a small reservoir.
- There is some kind of conveyance that provides the water to the turbine. In the illustration above, this is done by a penstock, which is often made of PVC pipe. This could also be done by a channel.
- The water spins a turbine, which spins a generator, which provides electricity. This is all contained in the powerhouse in the image above. There are a number of different types of turbines, most of which require a jet of water that is sprayed through a nozzle at the end of the penstock. If you are interested, see details in this reading from the U.S. DOE.
Energy and Power in Water
As described above, the kinetic energy in flowing water starts out as gravitational potential energy. The gravitational potential energy of a given amount of water at any elevation can be calculated using the following equation:
- Pe = m x g x h
- Pe = potential energy in Joules
- m = the mass of the water in kg
- g = the acceleration due to gravity (m/s2)
- h = the height of the water in m (usually called the "head")
The force of gravity is essentially a constant (it gets a little bit smaller with height). Thus, all else being equal, as height and mass increase, the potential energy increases. Keep in mind that this equation only illustrates the maximum kinetic energy available to a hydropower system. In reality, there are always losses by the time the kinetic energy is converted to electricity.
The power available in water at height is given by a similar equation:
- P = Q x g x h
- P = power in watts
- Q = discharge of water in kg/s (this is also mass per unit time)
- g = acceleration due to gravity (m/s2)
- h = head (m)
Again, this is only the hypothetical maximum - it is impossible to capture all of this power in a turbine. This equation is almost the same as the potential energy equation - you just substitute discharge for mass. Since the discharge is kg/s, or mass divided by time, if you compare the two equations, the power equation is the energy equation divided by seconds. This makes sense if you think about it: the potential energy is given in Joules, and the power equation is given in watts. Recall that 1 J/s = 1 W. Makes sense, right?
Calculating Microhydro Output
It turns out that calculating the approximate power output of a microhydro system is not terribly difficult. According to the U.S. DOE, a typical system has an efficiency of about 53%. This includes losses from the nozzle, the wiring, the generator, and a few other things. The power of a microhydro system with this efficiency is approximately:
- power = net head x flow /10
- power = electric power in W
- net head = the gross head in ft including the head loss in the penstock
- flow = flow of water in gal/min
- 10 = conversion factor (this can range from 8 - 12, with 10 being about average)
To determine the gross head, you measure how many feet above the generator the penstock starts. Note that this is not the same as the length of the penstock. The penstock is sloped, and thus will be longer than the head. The head loss is based on a few factors, including the diameter of the penstock, the pressure inside the penstock, and the number of turns and fittings there are in the penstock. According to Homepower Magazine, 30% is a typical amount of head loss, which means you would calculate the gross head time 0.7 to determine the net head. The flow of a stream through a penstock can vary wildly, from a few gallons per minute to a few hundred (or more). To provide some context a garden hose usually has a flow of about 20 gallons per minute, though this can also vary significantly depending on a number of factors.
Let's say I have a property in which I can create a diversion channel and forebay 100 ft above a power house, and I measure my flow at 50 gpm. Assuming a good system design which includes a head loss of 30%, my output would be:
- power = net head x flow / 10
- power = 100 ft x 0.7 x 50 / 10 = 350 W
- If I could get this to operate all day, I would get (350 W x 24 h/day = ) 8400 Wh or 8.4 kWh/day
Further Reading/Viewing
This lesson only scratches the surface of microhydro systems. There are many designs and factors to consider. Each site is different. For a more detailed explanation, see this website from the U.S. DOE, and for a good case study, see this example from Homepower Magazine (starting on p. 32). There are dozens of videos on YouTube that detail specific systems, many of which are worth checking out if you are interested.
If you are interested in learning more about the power and energy available in water for hydroelectric, see this video presentation I put together for another course.