Overview

Meteorologists are often so busy looking at weather maps for 850 mb and above that they don’t pay attention to what is happening near Earth’s surface. Yet we walk on Earth’s surface and we live in the air near Earth’s surface, which is called the planetary boundary layer (PBL). The PBL has repeatable cycles from day-to-day, but it also has chaotic, turbulent behavior that cannot easily be described by mathematics and certainly cannot be predicted. These repeatable cycles and chaotic behavior have a huge impact on the quality of the air that we breathe and on the sources of sensible heat and water vapor that are essential for the weather above the PBL. In this lesson, we will show how the PBL rises during the day and drops down at night. This behavior is driven by turbulent motion, so we will see how all motion can be separated into the mean flow and the turbulent flow using some simple concepts, including Reynolds averaging. We will see that while the mean wind is most important for moving water vapor and momentum horizontally, turbulent transport is most important for moving these quantities and others vertically throughout the PBL to the base of the free atmosphere above it. We will see how turbulent eddies of different sizes are related and which ones have the most energy. Finally, we will take a look at the energy budget for different types of locations and different times of day. Hopefully you will understand that while weather forecast models treat the planetary boundary layer as a boundary condition, the atmosphere treats it as an integral part of weather.

Learning Objectives

By the end of this lesson, you should be able to:

• draw the PBL and its diurnal variation
• perform Reynolds averaging on an equation and derive an equation for the turbulent parts
• explain kinematic fluxes
• show vertical motion using eddy fluxes
• explain turbulent kinetic energy (TKE) and its behavior
• sketch the surface energy budget for different conditions

Questions?

If you have any questions, please post them to the Course Questions discussion forum. I will check that discussion forum daily to respond. While you are there, feel free to post your own responses if you, too, are able to help out a classmate.

11.1 The atmospheric boundary layer is your home.

The atmospheric boundary layer (ABL) is the tropospheric layer that is directly influenced by the presence of Earth’s surface and responds to surface forcings in an hour or less. It is also called the planetary boundary layer or just the boundary layer. The atmospheric boundary layer is typically 1 km deep during the day and ~100 m deep during the night. Above the boundary layer is the free atmosphere. We live in the atmospheric boundary layer.

Mid-day planetary boundary layer over different surfaces.

Credit: NOAA Earth System Research Laboratory

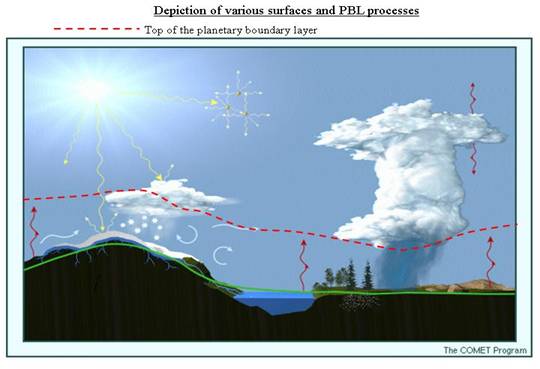
The surface forms a boundary for the atmosphere and is actually responsible for the existence of the planetary boundary layer.

The surface influences the atmosphere in four main ways:

• sensible heat flux
• moisture flux
• momentum flux, also called frictional or turbulent drag (see section 10.10)
• radiation

The water vapor that is in the air came from the evaporation of liquid water or sublimation of ice in or on the surface. Once that water vapor is in the atmosphere, it can condense, thus providing energy that heats the air and creates buoyant energy, as you learned in Lesson 3.

The picture below was taken on a sunny summer day over Maryland. What do you see? Starting at the bottom, you can barely make out the buildings and the roads because the air is so uniformly hazy. The haze extends all the way up to the lower parts of the fair weather cumulus clouds, which seem to be bobbing on top of the haze, like Styrofoam peanuts bobbing on top of a pool of water. Above the clouds, it’s blue sky with some thin cirrostratus clouds. This haze layer is the atmospheric boundary layer and the fair weather cumulus clouds mark its top.

Fair weather cumulus riding on top of a hot hazy summer atmospheric boundary layer, somewhere over Maryland.

Credit: W. Brune

Where did the haze come from? How did the clouds form? How did the haze get to be so uniform? Why are the fair weather cumulus clouds bobbing on top with blue sky above? You already know answers to the first two questions. The haze is small particles that came from the surface or were made in the atmosphere by gas-to-particle conversion and then swelled in the hot humid air. The clouds come from moist air containing aerosol that rises and cools until its supersaturation is sufficient to form cloud drops. The condensation releases energy, creating buoyancy, and the clouds rise until they reach their level of neutral buoyancy (LNB). You will learn in this lesson why the haze is so uniform (turbulent mixing) and why the clouds bob on top (a stable layer with increasing potential temperature above the boundary layer).

There are three basic ways that air can be moved: the mean wind, waves, and turbulence. You have already learned about the mean wind and its causes, but mostly we have dealt with the wind in the free troposphere. In the boundary layer, transport of moisture, heat, and momentum are dominated by the mean wind in the horizontal and by turbulence in the vertical. Turbulence is a much more persistent part of boundary layer flow than it is of flow in the free atmosphere.

For any variable over time or space, we can split that variable into two values—the mean and the perturbation. We will see more about this later.

Turbulent transport consists of swirling motions called eddies. These eddies occur in a range of sizes, and they can have different intensities, meaning wind velocities. We can plot the turbulent intensity as a function of size of the eddies to get a turbulence spectrum. To get an idea about the behavior of eddies and clouds, watch the following short video of cloud formation.

11.2 A Day in the Life of the Boundary Layer

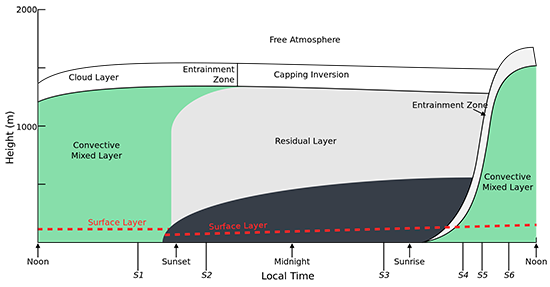
The boundary layer is not frozen in time but instead changes dramatically during the course of the day. Let’s start with the midday when the boundary looks like the hazy scene over Maryland (figure in 11.1). The boundary layer consists of a mixed layer that is stirred by solar heating of the surface and convection of warm moist air that pops up sporadically from place-to-place and time-to-time, and, as a result, mixes the air within the boundary layer. This convective stirring takes about ten to twenty minutes to go from bottom to top. As the air bubbles up, it mixes with the air surrounding it and with the air from the free troposphere at the top, thus creating an entrainment zone, which is where the clouds are.

As the sun sets, the solar heating of the surface and the convection and associated turbulent eddies cease. Air from the surface no longer mixes with air throughout the convective boundary layer, and the air that was mixed during the day stays above the much lower nighttime stable boundary layer in a layer called the residual layer. Any gaseous or particle emissions from the surface are trapped within this nocturnal boundary layer. Because convection ceases at night, the winds in the residual layer are no longer affected by turbulent drag at Earth's surface and they accelerate in the presence of a horizontal pressure gradient, sometimes forming a supergeostrophic flow called the nocturnal jet. 

Turbulent drag at Earth's surface is the primary source of mixing in the shallow nighttime boundary layer. Turbulent eddies in the nighttime stable boundary layer often have about 1/10^th the velocity of the eddies that occur in the daytime convective boundary layer. The impact of these weak turbulent motions is countered by the tendency of radiation to cool Earth's surface at night. Sometimes the wind shear at the top of the nighttime boundary layer creates some instability and turbulence within the nighttime boundary layer. Unlike the vigorous deep covective boundary layer found during the day, the nighttime stable boundary layer is shallow, about 1/10^th the depth of the daytime boundary layer and has weak intermittent turbulence and temperatures that fall during the night due to radiative cooling.

In the morning, the sun returns to heat the surface and to start driving convection and mixing again. This convection bubbles up, bumping into and entraining air from the residual layer. As the solar heating increases, the convection has more energy and can rise higher and entrain more air from the residual layer. Eventually, the daytime convection warms the boundary layer to its maximum temperature and this maximum temperature determines the height to which the convection will penetrate into the stable free atmosphere above the boundary layer.

Diurnal evolution of the atmospheric boundary layer. The black region is the stable (nocturnal) boundary layer. Time markers S1–S6 are used in lesson 11.3. After R. B. Stull's An Introduction to Boundary Layer Meteorology (1988).

Credit: NikNaks (Own work, based on [1]) [CC BY-SA 3.0], via Wikimedia Commons

The following video explains the variation of the planetary boundary layer over the course of a typical day:

11.3 The Story of Diurnal Boundary Layer Growth Told in Vertical Profiles of Virtual Potential Temperature

Recall the concept of virtual potential temperature, which was introduced in Lesson 2. The virtual potential temperature is found by replacing the temperature in the formula for virtual temperature with the potential temperature:

θ_v is the virtual potential temperature. It is a useful quantity because it takes the moisture into account as well as temperature when considering buoyancy and stability. Thus, adiabatic ascent or descent in moist air follows the constant virtual potential temperature line all the way up to the lifting condensation level (LCL), where the potential temperature increases. So let’s look at the evolution of the profile of virtual potential temperature in a cloud-free boundary layer.

Boundary layer diurnal evolution as told by virtual potential temperature profiles. For context, see figure in lesson 11.2. ML = mixed layer, FA = free atmosphere, SBL = stable boundary layer, RL = residual layer. See S1 = late morning, S2 = just after sunset, S3 = just before sunrise, S4 = just after sunrise, S5 = mid-morning, S6 = late afternoon. From R. B. Stull's An Introduction to Boundary Layer Meteorology (1988).

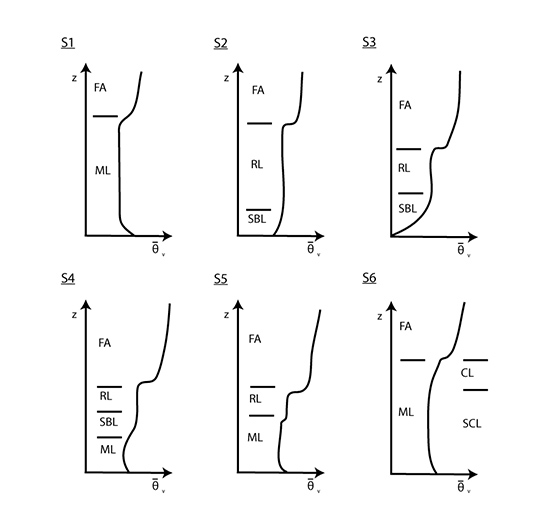
Start with the late afternoon (S1 above). Surface heating causes the air near the surface to have a higher virtual potential temperature than the air just above it, so that the air is superadiabatic. Thus, air parcels of this warm moist air rise into the mixed layer, warming this layer of air. Some of the warm moist parcels (also called convective eddies) rise all the way up to the point in the free atmosphere where the virtual potential temperature is as great or greater than the air parcel’s value. At this point the air parcel likely mixes with the surrounding air.  Mixing the warm free-tropospheric air into the mixed layer, which is called entrainment, also causes the daytime mixed layer to warm. Turbulent drag at Earth's surface also contributes to the turbulence in the boundary layer. The result of this vigorous convective activity is a well-mixed boundary layer.

Just after sunset (S2 above), the surface cools by infrared radiation [1]and the air near the surface becomes thermodynamically stable with a virtual potential temperature (and thus temperature) inversion. As in the day, turbulent drag at Earth's surface creates turbulent mixing, but the air's thermodynamically stability suppresses this vertical mixing. As a result, the nocturnal boundary layer on a calm night becomes quite stable, and, as the surface continues to cool, the boundary layer becomes even more stable during the night (S3 above). On a windy night, the nocturnal layer is closer to well-mixed, but only if the turbulent drag is strong enough to counter the infrared radiative cooling at Earth's surface. The stable boundary layer grows, not by convective mixing, but by turbulent drag at Earth's surface and sometimes by shear-drive mixing at the top of this layer.

Just after sunrise (S4 above), the surface is warmed by the sun, and as it continues to get warmed throughout the morning (S5 above), convection begins to mix warm air up first throughout the stable boundary layer and then into the mixed layer. Any trace atmospheric constituents left in the residual layer from the day before are now mixed back into the boundary layer as it grows higher. Finally, the residual layer is entirely mixed into the growing boundary layer, and the boundary layer returns to its condition of the previous afternoon (S1 above). If conditions are right, a convective cloud layer may form at the top of the mixed layer (S6 above).

Air pollution over Cairo, Egypt.

Credit: Nina Hale [2] via flickr

Think about morning and evening rush hours. During morning rush hour, which is near sunrise, the vehicle emissions mix into a shallow boundary layer and hence the mixing ratios of the pollutants can be quite substantial. This situation leads to the photochemistry that makes pollution, including ozone. In the evening, the rush hour traffic also emits the same amounts of pollutants into the boundary layer, but because the boundary layer height is so much greater in the early evening than in the morning, the pollutant mixing ratios are less because the same level of emissions are being mixed into a larger volume of air. Thus the effects of evening emissions are not as severe as the effects of morning emissions. In addition, modeling the planetary boundary layer height correctly is essential for accurate air quality modeling.

Also think about the development of convective storms. Summertime thunderstorms are most common in the afternoon and evening because many of these storms are initiated by the convective eddies in the daytime mixed layer. As the mixed layer grows, the turbulence can reach the lifting condensation level, which the level at which clouds form (see Lesson 3) and, under the right conditions, the level of free convection (again, see Lesson 3), which is the level at which convective storms begin to grow. The growth of the boundary layer is thus closely connected to the initiation of convective storms.

The diurnal variation of the planetary boundary layer height is more than just a curiosity--it has influence on our daily lives and health because we live, work, and breathe mostly in the atmospheric planetary boundary layer. Thus it is important that meteorologists and atmospheric scientists gain a better understanding of the atmospheric motions and energy budget of the planetary boundary layer. Gaining this understanding means learning something about atmospheric turbulence, which is the small-scale chaotic winds created by the interactions of the planetary boundary layer with Earth's surface.

11.4 Frozen: The Taylor Hypothesis

We would like to be able to take snapshots of the eddies in three dimensions and measure all their sizes each instant. Unfortunately, we do not have a good way to do this. Instead, we can simply measure the fluctuations of a variable such as wind speed, specific humidity, or temperature with a sensor at one location for a period of time. In this way, we watch the eddies drift by the sensor. But the eddies could be changing size and shape as they drift by the sensor. Let’s put this physical concept in the context of the total derivative.

Take a variable like temperature, T. We know that the change in T with time at any location (such as where a sensor might be placed) is the sum of the total derivative and the temperature advection:

The temperature advection is the change in temperature at the sensor due to the advection of warmer or colder air past the sensor. The total derivative is the change in temperature of an air parcel moving past the sensor. Such a temperature change may be caused by any number of processes, such as the absorption or emission of radiation, condensation or evaporation (latent heating or cooling), or compression and expansion. Taylor’s hypothesis says that we can assume that the turbulent eddies (which we can think of as the circulation of air parcels) do not significantly evolve, or are "frozen", as they advect past the sensor and thus the change in temperature within each eddy is negligible:

so that:

Local temperature gradients, which might be present from one side of an eddy to another, are advected across the sensor by the mean wind without the eddy changing.

When is this condition valid? Experiments suggest that this hypothesis is valid when the variation of the wind speed due to turbulence is less than ½ of the mean wind speed.

Why is this hypothesis, or maybe more precisely stated, this approximation, useful? It is commonly used to infer the sizes of turbulent structures from observations of turbulence taken over a period of time. If this approximation hold true, the size of the turbulent eddy can be estimated by multiplying the time it takes an eddy to pass by a sensor by the mean wind speed that is "carrying" this "frozen" eddy. Thus eddy size equals eddy advection time multiplied by the mean wind. This approach has proven to be very useful for understanding the structure of turbulence.

We start this study with methods to separate wind motion driven by larger scale processes, such as gradient flow or geostrophic flow, from turbulence.

Anemometers. A cup anemometer and wind vane are on the left. A sonic anemometer, which uses sound to measure vertical as well as horizontal winds more than ten times a second, is on the right. You may have seen sonic anemometers at state weather stations along highways. Sonic anemometers are so fast that they are great for measuring turbulence and turbulent transport.

Credit: Department of Energy Atmospheric Radiation Measurement Carbon Program

11.5 Here’s How Reynolds Did Averaging

For any variable, the observed value can be written as a sum of the mean value and a turbulent value. The turbulent part is sometimes called the fluctuating part or the perturbation. For example, we can write the zonal component of the velocity as:

where $\overline{u}$ is the mean, or average value, and $u^{\prime }$ is the turbulent part.

The average can be a spatial average or a temporal average. Mathematically, we can write those averages using integration if we have continuous data or by summation if we have discrete data. Here are the formulas for computing the mean of the zonal component of the velocity:

where the integrals are over specific time periods or distances and the summations are for N discrete measurements. If the turbulence does not change with time and is homogeneous (i.e., the same in all directions and for all time), then these averages equal each other. It is important to remember that the mean values defined in the above equation are not necessarily constant in space or time. 

In Lesson 10, we developed the equation of motion without really considering the short-term and small-scale variations, except to say that they led to turbulent drag, which acts to resist the mean flow in the upper boundary layer. Now we want to think about how to correctly capture the dynamic effects of turbulent motion. What we want to do is to write down the equations of motion that you learned in Lesson 10; substitute mean and turbulent parts for the variables such as u, v, and w; average over all the terms; and then see if we can sort out the terms to create an equation for the mean wind and an equation for the turbulent wind. This type of averaging is called Reynolds averaging.

But first we need to learn the rules for averaging.

Rules of Averaging

These rules should make sense to you. For example, consider the first rule, which says that the average of the turbulent value is zero. That makes sense because the turbulent value is defined as the departure from the mean. Now let’s apply these rules to a variable with a mean and a turbulent part. For example, consider the product uv, which is just the advection of horizontal wind in one direction by the horizontal wind in the other direction.

So, using the rules:

This second term, a product of two turbulent terms is not necessarily zero! Whereas the average of one turbulent term is zero by definition, the average of the product of two turbulent terms is not necessarily zero.

The following video (3.11) further describes Reynolds averaging:

Example

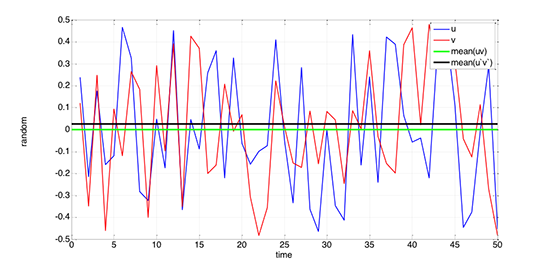
Consider two random numbers varying between –0.5 and 0.5, called u and v. The figure below shows u, v, the mean of uv and the mean of u’v’. Of course, the mean of u’v’ might be zero, but is it not necessarily zero, as shown in this figure.

Time series of two random variables whose means are zero (u in blue and v in red). The green line is the product of the mean of u and the mean of v; this product equals zero. The black line is the mean of the product u'v'; this product is not zero!

Credit: W. Brune

The same thinking applies to u².

Remember your statistics and the concept of variance:

So, the variance is the same as the mean value for the square of the turbulent part of the variable.

The covariance of u and v is given by the equation:

The standard deviation is just:

We can get a better sense of how large this variance is by dividing by the mean value:

11.6 How Kinematic Fluxes Move Air Vertically

Now that we know how to separate out the mean and turbulent parts, we can look at the concept of kinematic flux.

A flux is the transfer of some variable per unit area per unit time. Generally in meteorology, we care about variables like mass, heat (i.e., temperature), kinetic energy, moisture, and momentum. Those who study the atmosphere's composition are also interested in the flux of chemicals emitted into the atmosphere from the surface and the flux of atmospheric pollutants, such as ozone, back to Earth's surface. For this discussion, let's consider only the fluxes directly relevant to meteorology.

The SI units of fluxes would be ${\text{kg m}}^{-2}{\text{ s}}^{-1}$ for mass (m); ${\text{kg}}_{\text{water}}{\text{ m}}^{-2}{\text{ s}}^{-1}$ for moisture (m_v);  $({\text{kg m s}}^{-1}){\text{ m}}^{-2}{\text{ s}}^{-1} ={\text{ kg m}}^{-1}{\text{ s}}^{-2}$ for momentum (mv), and  ${\text{J m}}^{-2}{\text{ s}}^{-1}$ for heat (mc_pT_v) or ${\text{W m}}^{-2}$ (just like radiation).

We can write these in the kinematic form by dividing by the density of air:

$\text{kinematic mass flux}=({\text{kg m}}^{-2}{\text{ s}}^{-1})/({\text{kg m}}^{-3})={\text{m s}}^{-1}$

$\text{kinematic moisture flux = }({\text{kg}}_{\text{water}}{\text{ m}}^{-2} {\text{s}}^{-1})/({\text{kg}}_{\text{air}} {\text{m}}^{-3}){\text{ = kg}}_{\text{water}}{\text{ kg}}_{\text{air}}{}^{-1} {\text{m s}}^{-1}$

${\text{kinematic momentum flux = kg m}}^{-1}{\text{ s}}^{-2}/(\text{kg} {\text{m}}^{-3}){\text{ = m}}^2{\text{ s}}^{-2}$

For kinematic heat flux, the heat flux is usually divided by the air density times the specific heat of air to give units of $({\text{J m}}^{-2}{\text{ s}}^{-1})/({\text{kg m}}^{-3}{\text{ J kg}}^{-1}{\text{ K}}^{-1})={\text{K m s}}^{-1}$. Note that this is just a temperature times a velocity.

The word “kinematic” is often dropped and assumed.

The expression for the vertical flux of potential temperature is just equal to the vertical wind times the potential temperature, so the Reynolds average of that flux is:

The first term on the right is the vertical flux of potential temperature due to the average vertical motion, but w ~ 0 on average in the boundary layer, so we can usually drop the first term on the right.

Let’s consider how this flux works at moving thermal energy. A typical condition for the mixed boundary layer is a superadiabatic layer near the heated surface (i.e., θ decreases with height).

How turbulence is able to move heat vertically by turbulent heat flux for the daytime case with surface heating. Subscripts p and e refer to parcel and environment, respectively. θ' is always θ of the parcel before it moves minus θ of its new environment at its new height. Eddies move air both down (left panel) and up (right panel). In both cases, the net heat flux is up. Note that eddies cycle in the vertical and so they typically move air both up and down as shown in the panels at the same time.

Credit: W. Brune

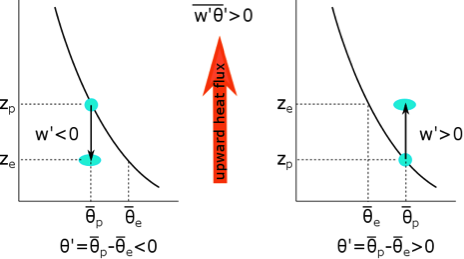
Let’s look at the different cases.

Daytime case with surface heating such that $\partial \theta /\partial z<0$ (as in figure above). Eddies can make air trade places. They move some air parcels down,

for $w\text{'}<0\text{ and }\theta \text{'}<0:\overline{w\text{'}\theta \text{'}}>0$

and at the same time move some up,

for $w\text{'}>0\text{ and }\theta \text{'}>0:\overline{w\text{'}\theta \text{'}}>0$

Both of these processes are happening simultaneously. If the air parcels mix at their new heights, they move cooler air lower (left panel above) or warmer air higher (right panel above); in both cases they move heat up. Thus, when the potential temperature decreases with height (i.e., is superadiabatic), the turbulent eddies move warmer air up and the heat flux is positive (i.e., upward, which is the positive z direction).

How turbulence is able to move heat vertically by turbulent heat flux for the nighttime case with surface cooling. Subscripts p and e refer to parcel and environment, respectively. θ' is always θ of the parcel before it moves minus θ of its new environment at its new height. Eddies move air both down (left panel) and up (right panel). In both cases, the net heat flux is down. Note that eddies cycle in the vertical and so they typically move air both up and down as shown in the figures at the same time.

Credit: W. Brune

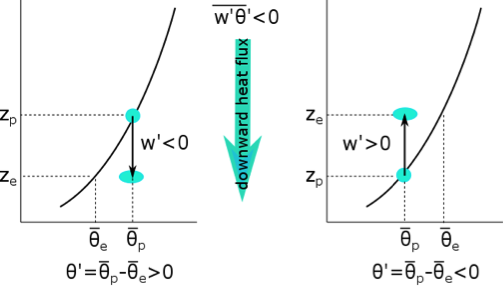
Nighttime case with surface cooling such that $\partial \theta /\partial z>0$ (see figure above). Eddies make air parcels trade places vertically. They move some air parcels down,

for $w\text{'}<0\text{ and }\theta \text{'}>0:\overline{w\text{'}\theta \text{'}}<0$

and some up,

for $w\text{'}>0\text{ and }\theta \text{'}<0:\overline{w\text{'}\theta \text{'}}<0$

Both of these processes are happening simultaneously. If the air parcels mix at their new heights, they either move warmer air lower (left panel above) or cooler air higher (right panel above); in both cases they move heat down. Thus, when the potential temperature increases with height (i.e., is subadiabatic), the turbulent eddies move warmer air down and the heat flux is negative (i.e., downward, which is the negative z direction).

We see that by turbulent motions, the thermal energy tends to flow from higher mean temperature to lower mean temperature, or to put it another way, down the gradient of the mean value.

So, the heat flux $\overline{w\text{'}\theta \text{'}}$ tells us about the transport of thermal energy by eddies. Note that the transport is in the direction from the higher values to the lower values for the mean potential temperature. The heat flux is the way that sensible heat gets transferred to the free troposphere in the atmosphere's energy budget [1]. The heat flux combined with the moisture flux create conditions that can lead to thunderstorms and severe weather.

Watch the following video (1:49) for further discussion of the eddy heat flux:

11.7 Can we relate this turbulent flux to a molecular flux?

You have already encountered the idea of molecular fluxes in cloud physics, in the section on vapor deposition [3]. Water vapor molecules are moving randomly all the time, but when water vapor molecules hit a liquid or ice surface and stick, the water vapor concentration near the drop is less than it is farther away. As a result, molecular diffusion tends to move water vapor from regions of higher water vapor concentration far from the drop towards regions of lower water vapor concentration near the drop. The greater the difference between the concentration far away from the drop and the concentration near the drop, the greater will be the flux of water molecules to the drop.

where $F_{molecules}$ is the molecular flux (SI units of molecules m^–2 s^–1), $\partial n/\partial r$ is the change in concentration $n$ (SI units of molecules m^–3) as a function of radial distance $r$ from the drop (SI units of m), and $D_v$ is the molecular diffusion coefficient (SI units of m² s^–1). When $n$ increases with $r$, then the flux is negative, which means that the flux is toward the drop, in the negative $r$ direction.

Molecular diffusion, by the way, is very slow at transferring molecules from one place to another in the troposphere. By solving the equations of motion for a simple case, we find that the characteristic time to travel a distance L by molecular diffusion is:

Molecular diffusion cannot transport anything fast enough for the atmosphere except on small scales of a centimeter or less. However, on the spatial and temporal scales of the planetary boundary layer, eddies are quite effective at moving heat, molecules, and momentum. In the last section, we saw that turbulence tends to move heat from heights where the air is warmer to heights where the air is cooler. Eddy "diffusion" shares this characteristic with molecular diffusion.

We can write the heat flux in the same way that we write the molecular flux:

where K is the eddy diffusion coefficient. Since K is always positive, this equation makes it clear that the flux of any quantity goes from where there is more of that quantity to where there is less of that quantity.

11.8 Let’s see how vertical turbulent transport can be quantified.

Let’s go all the way back to the idea of advection [4] in Lesson 8.7. We will replace the scalar R with potential temperature:

After taking the Reynolds average, we achieve the equation:

The term on the left is the rate of change of the mean potential temperature at a given height, although it applies to any height. The first term on the right is the local heating from the divergence of the radiant energy and from phase changes. This term is generally small, except in clouds, so we can ignore it in the typical convective boundary layer. The second term on the right is the mean advection, but can typically be ignored in the fair-weather boundary layer. Scale analysis shows that the mean horizontal advection (ignored here for the moment) is usually quite large, and must be kept in the heat conservation equation.

If we assume that the density does not change, then we can basically say the volume of air doesn’t change (i.e., incompressibility). We used this concept to show that horizontal convergence results in vertical divergence [5]. For the typical convective boundary layer, turbulence is fairly homogeneous, meaning that the velocity perturbations do not vary much in space (i.e., are about equal in the x, y ,and z directions). Thus, w' is independent of z, which means that w' can be taken inside of the derivative in the third term on the right of Equation [11.10]. With the assumptions described above for a fair-weather convective boundary layer, we now have:

What does this mean? It means that the change in the boundary layer potential temperature in the daytime boundary layer is driven by the negative of the vertical gradient of eddy flux of thermal energy. During the day, the eddy heat flux is greatest at the surface and decreases with altitude.  So $\frac{\partial \left(\overline{w^{\prime }{\theta }^{\prime }}\right)}{\partial z}<0$ , which means that the mean potential temperature increases with time ($\frac{\partial \overline{\theta }}{\partial t}>0$). At night, the opposite is generally true.

Consider the sensible heat flux, F_SH (SI units of W m^–2). As we saw in the average atmospheric energy budget, the sensible heat flux plays an important role.

The average θ is often approximately constant over the height of the boundary layer. So, when we integrate both sides of Equation [11.11], we get the following:

Example

We can put some numbers to these values to show how temperature changes from turbulent eddy fluxes alone. Reasonable values for the boundary layer depth and daytime surface kinematic heat flux are 1000 m and 0.2 K m s^–1, respectively. Thus,

So, the boundary-layer potential temperature (and thus the temperature) is increasing during the day at a little less than 1 K hr^–1.

Thus, the heating of the boundary layer is driven by the eddy heat flux from the surface. In this way, the heating at the surface due to the absorption of solar energy at Earth's surface is spread throughout the boundary layer.

11.9 What other fluxes are important?

We have focused on the sensible heat flux up to now, but turbulence creates other vertical fluxes. There are many vertical turbulent fluxes, but two important ones are the latent heat flux, which involves the vertical transport of water vapor, and the horizontal momentum flux, which involves the vertical transport of horizontal wind.

Latent Heat Flux

For the purpose of this discussion, use the specific humidity, q. There is the mean value for q at different heights, and then there is the kinematic eddy flux. Using the same methods as before, we find that the kinematic water vapor flux (or specific humidity flux) is given by:

This flux has SI units of ${\text{kg}}_{\text{water}}{\text{ kg}}_{\text{air}}{}^{-1}{\text{ m s}}^{-1}$. Usually the specific humidity is greatest near Earth's surface and decreases with height, largely because most of Earth's surface is covered with water. Using the same logic as for the sensible heat flux, we expect a flux of water vapor from the surface, where the specific humidity is greater, into the boundary layer.

However, we usually want to compare energy fluxes caused by different processes as in Lesson 7.3 [1], so we multiply the specific humidity flux by the terms necessary to convert it into an energy flux that would result from the condensation of that water vapor. We end up with a latent heat flux:

with SI units of $({\text{kg}}_{\text{air}}{\text{ m}}^{-3})({\text{J kg}}_{\text{water}}{}^{-1})({\text{kg}}_{\text{water }}{\text{kg}}_{\text{air}}{}^{-1}{\text{ m s}}^{-1})={\text{J m}}^{-2}{\text{ s}}^{-1}$.

Note that we have multiplied the specific humidity flux by the density of air and the latent heat of vaporization to put the specific humidity flux in terms of an energy flux, which we see is comparable to the sensible heat flux and is a significant fraction of the global energy balance at Earth’s surface. In fact, on a global scale, the latent heat flux is about five times larger than the sensible heat flux and is about half the total absorbed solar irradiance.

Latent heat flux is the primary way that water vapor gets into the atmosphere and is thus the primary source of water vapor for convection and clouds. Predicting convection and precipitation depends on knowing the latent heat flux. The relese of this latent heat aloft, where water vapor condenses into clouds and precipitation, has a dramatic impact on atmospheric dynamics.

Predicting latent heat flux at Earth's surface can be challenging, especially over land where the interactions among the vegetation, soil, and atmosphere can be complex. You can think of plants as complicated "water miners" that extract water from the soil, try to hold onto it, but lose some of it to the atmosphere through their pores.  These processes strongly influence the atmosphere. The field of ecohydrology seeks to improve the understanding of this complex and critical element of the Earth system. 

Horizontal Momentum Flux

The mean horizontal wind velocity is the vector sum of the wind components in the x-direction and the y-direction. The magnitude of the mean horizontal wind velocity is given by:

The horizontal momentum flux is basically vertical turbulent eddies bringing high-wind-velocity air down from above. You all have experienced this phenomenon if you have ever been out early in the morning, just as the solar heating of the surface has begun to create convection and mix calm near-surface air up and windier residual layer air down.

The equations for the (kinematic) vertical fluxes of x-momentum and y-momentum air are, respectively:

where the SI units are m² s^–2 and where u' and v' are wind speed perturbations in the x and y directions, respectively.

Note that the horizontal wind speed, V, is zero at Earth's surface (because of molecular friction) and increases with height. Just as the turbulent heat flux moves air with a higher potential temperature to heights where the potential temperature is lower, the turbulent momentum flux moves air with higher horizontal momentum (i.e., horizontal velocity) to heights where the mean horizontal momentum is lower. That is, the horizontal momentum is moved downward through the boundary layer to the Earth's surface, where it is dissipated by molecular friction.

Just as the heat flux is equal to a constant times the vertical gradient of the mean potential temperature (Equation [11.9]), the x-momentum flux is equal to a constant times the vertical gradient of the mean x-wind:

where K is the eddy diffusivity.

Just as the change with time of the mean potential temperature is related to the negative of the vertical gradient of the kinematic heat flux (Equation [11.11]), so is the change with time of the mean velocity related to the negative of the vertical gradient of the kinematic momentum flux. Thus, the x-component momentum equation in the boundary layer becomes (ignoring other terms for now, such as the pressure gradient force and the Coriolis force):

Just as we assumed the mean potential temperature is constant with height in the boundary layer, we can assume that the mean x-momentum (i.e., zonal velocity, u) is constant with height in the boundary layer. We can then integrate the above equation from the surface (z = 0) to the top of the boundary layer (z = h) and make the same assumptions about the flux at the top being relatively small to get:

where ${\left(\overline{u^{\prime }{w}^{\prime }}\right)}_0$ is the vertical flux of x-momentum at the surface.

These are the turbulent resistance terms that we introduced as friction in Lesson 10. They come from the downward transfer of horizontal momentum to the surface, where it is dissipated by molecular friction at Earth's surface. The deposition of momentum to the surface is a critical element in synoptic-scale flow, as noted in section 10.10 as well as being one of the key drivers of boundary layer turbulence.

As Equation [11.16b] indicates, this flux depends on the local eddy diffusivity and the local vertical gradient of the mean u velocity. The eddy diffusivity near the surface will increase as the mean wind speed in the boundary layer increases because vertical shear, which is responsible for the mechanical generation of turbulence, will be greater as the mean wind speed increases. Also, the vertical gradient of the mean u velocity near the surface will increase as the mean u of the boundary layer increases. Thus, we expect

The coefficient of proportionality is called the drag coefficient, $C_d$, which depends on the roughness of the surface and the thermal stability at the surface. Hence, combining Equations [11.16d] and [11.16e], we have for both horizontal components:

11.10 How do these fluxes look?

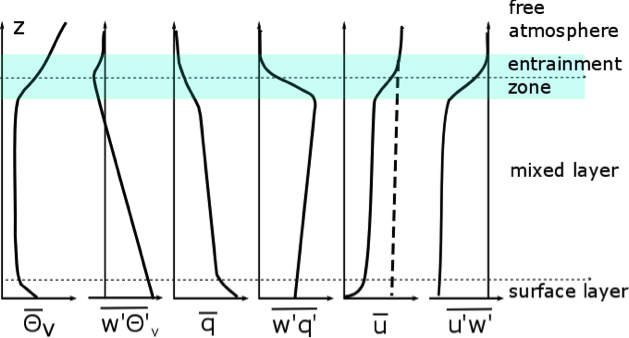
We have defined three mean variables, ${\overline{\theta }}_v$, $\overline{q}$, and $\overline{V_{}}$, and three eddy flux terms associated with these mean values, ${\overline{w\text{'}\theta \text{'}}}_v$, $\overline{w\text{'}q\text{'}}$, and $\overline{u\text{'}w\text{'}}$. Let’s examine their behavior as a function of height in the daytime boundary layer (see figure below).

The mean values and turbulent vertical fluxes of virtual potential temperature, specific humidity, and horizontal momentum for daytime conditions. The bottom solid line indicates the surface (z = 0). The top horizontal dashed line indicates the top of the boundary layer; the bottom horizontal dashed line indicates the top of the surface layer. The vertical dashed line is the calculated value of the geostrophic wind extending to the surface if there were no friction. The entrainment zone is an area of mixing between the mixed layer and the free atmosphere.

Credit: W. Brune, after Tennekes and Dreidonks, 1984

Virtual Potential Temperature, ${\overline{\theta }}_v$

The ${\overline{\theta }}_v$ profile is superadiabatic near the surface due to contact with the heated surface, neutral in the middle, and stable above. Eddies can rise from the surface to a height where ${\overline{\theta }}_v$ equals its surface value (assuming no cloud formation and condensation). The mixed layer will grow if surface heating or increased humidity by evaporation causes the surface ${\overline{\theta }}_v$ to increase, which means that air parcels can rise and be neutrally buoyant at greater ${\overline{\theta }}_v$ aloft and thus greater heights.

We see that the eddy flux ${\overline{w\text{'}\theta \text{'}}}_v$ is greatest at the surface, decreases nearly linearly with height, becomes slightly negative above the PBL height h because eddies are bringing warmer air down from above$\mathrm{}$. Remember, eddy fluxes carry a quantity like virtual potential temperature down the mean gradient. The eddy flux for virtual potential temperature (and all quantities) goes to very low values (essentially zero) above the entrainment zone even though a gradient is present because the eddy energy is much lower there.

Specific Humidity, $\overline{q}$

Specific humidity is greatest at the surface, where moisture sources, such as water bodies and vegetation, are present. The specific humidity falls off slowly with height until it reaches the PBL height, and then falls off rapidly into the free atmosphere. Because $\overline{q}$ falls off with height, the humidity flux $\overline{w\text{'}q\text{'}}$ is positive throughout the depth of the daytime ABL. Like all of the other turbulent fluxes, it is close to zero in the free troposphere becaue turbulence becomes weak and intermittent abouve the ABL. 

Horizontal Momentum Flux

$\overline{V_{}}$, the mean horizontal wind speed, increases logarithmically with height and then takes a jump above the PBL height as the wind no longer feels the friction from Earth’s surface and becomes geostrophic. The dashed line in the figure above indicates what the geostrophic wind would be without boundary layer friction. Because $\overline{V_{}}$is increasing with height, the horizontal momentum flux is negative throughout the boundary layer. It becomes less negative in the entrainment zone and approaches zero at heights above h.

So what does the daytime convective boundary layer look like? There are isolated convective updrafts surrounded by slower descending air, giving rise to the large-scale eddy circulation, as seen in the following video of the convective boundary layer, viewed from the top. Associated with the large eddies are smaller eddies that come about as the upward and downward air parcels move past each other. If you look closely, you will see eddies of all sizes in the video (:24), some quite large and some quite small, but the smaller ones seem to originate in the larger ones.

11.11 Turbulent Eddies: A Cascade of Energy

If an air parcel has a velocity, then it has kinetic energy. The air parcel's velocity can be broken down into average and perturbation parts and so can the kinetic energy. Now suppose we look at kinetic energy per volume of air: $\mathrm{½}\rho v^2$. Then we find the kinematic kinetic energy by dividing by the density.

If we start with the equation:

and we write each term as its mean and turbulent parts and then multiply all these terms out and take the Reynolds average, we can then apply the rules of averaging in Equation [11.1], and only two terms survive:

The first term is simply the kinetic energy associated with the mean wind. The second term is the kinetic energy associated with the turbulent wind and is called the turbulent kinetic energy, or TKE, for short.

Which size eddies have the most energy? We can look at the relative intensity of the different scales of wind by considering the energy associated with motions of different sizes. Remember that, by the Taylor hypothesis, the size of an eddy observed by a stationary sensor and the period of the eddy are related by the speed with which the eddies are sampled, which is the mean wind at a stationary sensor. Large eddies will have longer periods and smaller eddies have smaller periods.

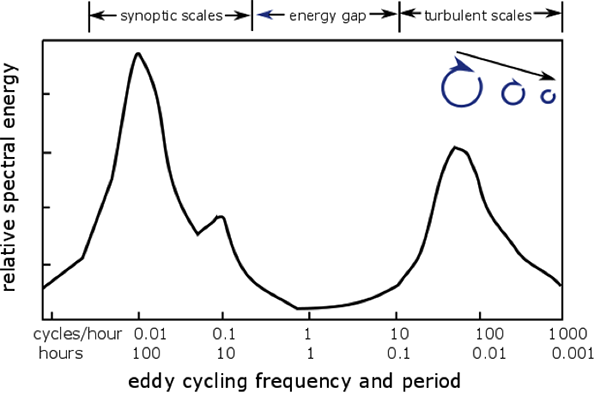
So, relative spectral intensity is just the amount of kinetic energy associated with that size eddy and the eddy size is associated with a period required for the eddy to pass over a sensor (see figure below).

• The peak in energy at 100 hours is from fronts and weather systems as they pass over a location. The spatial scale of these phenomena is relatively large and is called the synoptic scale.
• The smaller peak at about 24 hours is the diurnal cycle of wind speed, which increases during the day and then decreases at night.
• There is often a minimum in energy (called a spectral gap) at a time scale of an hour, where the circulations or eddies are relatively weak.
• This smaller peak at about 0.1 to 0.01 hours is called the “turbulent scale." This peak is caused by production of turbulent kinetic energy by buoyancy production (i.e., convection) and shear production (i.e., surface friction, the flux of momentum into Earth's surface). These eddies have the time scales of minutes and the size of the PBL.
• As the period of the eddies decreases below about 0.01 hours (about a minute), the strength of the eddies decreases.
• Eventually, on the subsecond time scale, the eddies have very little energy indeed.

Note that this figure is based on data taken close to Earth's surface. The peak energy at the turbulent scales will shift to lower frequencies and longer periods at greater heights above the surface. The maximum for ths "energy production scale" period is about 15 minutes and corresponds to convective eddies whose size is about as large as the depth of the daytime convective boundary layer. Turbulent energy production scales in the shallow stable nocturnal boundary layer are typically considerably smaller, with a maximum size that is about the depth of the noctural boundry layer, which is roughly 1/10^th that of the daytime convective boundary layer.

So what is happening? Energy is flowing from the larger-scale eddies to the smaller-scale eddies. Eventually, the energy is dissipated through viscosity, which is a molecular-scale process. So, the energy of the larger eddies is transferred into smaller eddies, and eventually that energy is lost to viscosity, which in turn generates heating.

Relative spectral energy (i.e., energy per unit frequency) as a function of eddy cycling frequency or time period. As eddies generated at the PBL scale by convection and shear break down into smaller eddies, the energy is dissipated.

Credit: W. Brune, after R. B. Stull's An Introduction to Boundary Layer Meteorology (1988), from a study of I. Van der Hoven (1957).

Lewis Richardson wrote a poem about this process for whorls (a.k.a. eddies) in 1922:

Big whorls have little whorls,

Which feed on their velocity;

And little whorls have lesser whorls,

And so on to viscosity

(in the molecular sense).

11.12 The Surface Layer’s Energy Budget

In Lesson 7, we looked at the energy budget of the average atmosphere. Now let’s look at the energy budget at Earth's surface. We can think of this budget in terms of energy fluxes and energy storage. As you learned in Lesson 2, energy is conserved—it must go somewhere.

There are several basic terms that we can put together in an energy equation that is appropriate for different environments or times of day. The units of the terms are W m^–2.

The main energy terms are:

•    R_net : radiation = (solar + atmospheric IR) - Earth IR (R_net > 0 heats Earth's surface).
• H : sensible heat flux (H > 0 heats the atmosphere).
• L : latent heat flux (L > 0 evaporation into the atmosphere).
• G : surface heating (G > 0 heats Earth's surface)
• S: energy storage in the layer between the height of turbulent flux and radiation measurements and the height of ground flux measurements (energy storage in the air, trees, buildings, and other structures and plants). This term is zero if all fluxes are measured right at Earth's surface. We will neglect this term to simplify the discussion.

Using these flux definitions, we can write an equation for the surface energy budget:

The ratio of sensible heat flux to latent heat flux is called the Bowen ratio:

It can be either positive or negative:

• > 10 over deserts,
• 2 – 6 over semi-arid lands or over crops and forests when the leaves are not out,
• 0.4 – 0.8 over grasslands and forests during growing season (the ratio is lower when water is abundant and higher when it is dry),
• < 0.1 over oceans,
• negative over oases.

Looking at this list, it is easy to see that the water vapor comes not only from the surface moisture but also from trees and other plants by a process called evapotranspiration.

Energy balance for four different common cases: (a) daytime, land; (b) nighttime, land; (c) daytime, a desert oasis; and (d) daytime ocean. Arrow lengths indicate relative magnitude of the different fluxes.

Credit: W. Brune (after R. Stull)

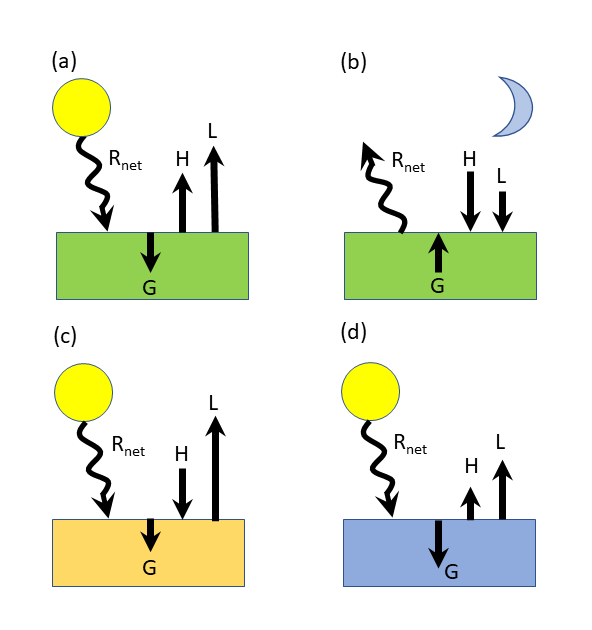
Look at the figure above, which shows the relative values of energy fluxes for different environments and times of day: 

• (a) daytime: solar heating dominates; heating is going into upward latent and sensible heating and warming the ground. The Bowen ratio (ratio of the sensible to the latent heat fluxes) depends on the amount of vegetation and surface moisture. The heating of the ground’s surface causes a downward energy flux into the ground.
• (b) nighttime: no solar shortwave; radiation is all infrared and is less than during the day, which has a net loss of energy to space. Both latent and sensible heat fluxes are negative because the ground is cooling and water vapor is condensing, leading to a positive gradient in temperature and specific humidity. The subsurface ground is warmer than the surface, so there is an upward energy flux from the subsurface to the surface.
• (c) daytime oasis with warm air advection over a moist surface: solar heating, sensible heat flux downward from hot dry air, latent heat flux upward offsetting some of the heating from the solar flux and the downward sensible heat flux. The surface is still heating, so some energy flux goes into the ground. The oasis is cooler than the surrounding desert because of the large latent heat flux.
• (d) daytime ocean: sensible and latent heat fluxes are positive, but much of the downward surface flux carries significant energy down into the ocean away from the surface. The ocean has a lot of heat capacity, so that solar energy can be absorbed in the ocean with little temperature change. Most of the energy goes into the ocean, with fairly constant fluxes of latent heat and sensible heat.

Summary

The atmospheric boundary layer has a strong diurnal cycle, which consists of a well-mixed layer that is ~1 km high during the day but collapses down to 10% of that at night, leaving behind a residual layer. The mixing is caused by turbulence, a chaotic mix of swirling eddies ranging in size from the height of the PBL to the size of your fist. Understanding turbulence is the key to understanding the motion of air in the PBL. Taylor’s Hypothesis shows that changes in eddy properties measured by a sensor in time can be used to describe the eddy properties in space.

Equations of motion by turbulent eddies arise from defining all quantities (e.g., wind speed, specific humidity, and potential temperature) in terms of their mean and turbulent parts, then substituting these two parts for each quantity into the appropriate conservation equations, expanding the equations, then taking the Reynolds averages. Terms with two turbulent components arise that are non-zero, and these give rise to turbulent fluxes of temperature, water vapor, and momentum. A key result is that eddies drive vertical transport of these quantities (and others) in the direction of where the mean quantities are the least from where they are the most. Furthermore, changes in the vertical profiles of mean quantities with time are caused by the vertical eddy fluxes of those quantities.

The energy in the PBL is a tale of the turbulent kinetic energy and the energy balance near the surface. Turbulence consists of eddies of all different sizes and lifetimes, ranging from sizes that are the height of the PBL to others as small as your fist. These eddies are related: the largest carrying the most energy, and the smaller ones fracturing off of the larger ones, thus cascading the energy from larger scales to smaller scales, ending eventually with molecular viscosity, which converts all that kinetic energy into heat. The driver of this turbulent kinetic energy is the exchange of energy at Earth’s surface and consists of net radiation, sensible heat flux, latent heat flux, and subsurface ground flux. Depending on the environment and the time of day, the relative values of these fluxes can be quite different, but in every case, the total energy budget must balance.

Reminder - Complete all of the Lesson 11 tasks!

You have reached the end of Lesson 11! Double-check that you have completed all of the activities before you begin Lesson 12.