5.7 Vapor Deposition
The growth of the cloud drop depends initially on vapor deposition, where water vapor diffuses to the cloud drop, sticks, and thus makes it grow. The supersaturation of the environment, senv, must be greater than sk for this to happen, but as the drop continues to grow, sk approaches 0 (i.e., eeq approaches es), so smaller amounts of supersaturation still allow the cloud drop to grow. Deriving the actual equation for growth is complex, but the physical concepts are straightforward.
- The growth rate (dmd/dt, where md is the mass of the drop) is proportional to senv – sk. Physically, this statement means that the greater the difference between the supersaturation in the environment and supersaturation at the drop’s surface, the faster water vapor will diffuse and stick on the surface. For instance, if senv equaled sk, then the evaporation and condensation of water on the drop’s surface would be equal and there would be no mass growth.
- As water vapor diffuses to the drop and forms liquid water, energy is released (i.e., latent heat of condensation) and this raises the temperature of the cloud drop surface, Tsfc, so that Tsfc > Tenv. But an outward energy flow occurs and is proportional to Tsfc – Tenv. Physically, this statement means that the drop and the air molecules around it are warmed by latent heat release. These warmer molecules lose some of this energy by colliding with the cooler molecules further away from the drop, and warm them by increasing their kinetic energy (see figure below).
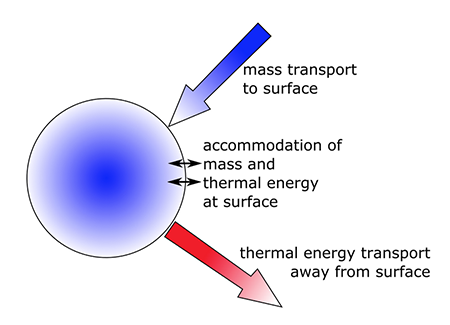
Schematic of the two physical processes in the growth of a cloud drop by vapor deposition. One is vapor deposition and the other is the transfer of condensational heating to the atmosphere;
Credit: W. Brune (after Lamb and Verlinde)
- When we account for both the flow of water molecules to the cloud drop surface and the flow of energy away from the surface, we can show that:
[5.14]
where G is a coefficient that is a function of T and p, ρl is the density of liquid water, and the other variables have already been defined. G incorporates the effects of the mass transport of water vapor molecules to the surface and the transport of heat generated on condensation away from the particle surface. Plugging in md = ρl4πrd3/3 to 5.14, taking the derivative, and solving for drd/dt, it is easy to show (try it!) that drd/dt is proportional to 1/rd. That is, the bigger the drop gets the slower it grows. Separating variables (rd and t) and integrating from rd = 0 at t = 0 to arbitrary values of rd and t reveals that rd is proportional to the square root of time:
rd = (Ct)1/2
[5.15]
where the constant C = 2G(senv – sk). The figure below shows how rd varies with time for a typical value of C, 4 x 10–13 m2 s–1.
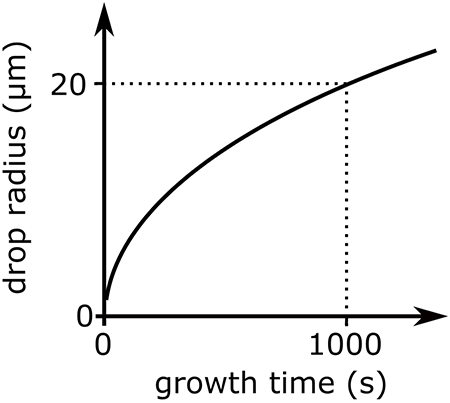
Growth of a cloud drop by vapor deposition as a function of time. Dashed lines indicate drop size after the typical cloud lifetime.
Credit: W. Brune
Physical explanation:
- The nucleated cloud drop radius increases fairly rapidly at the beginning, but within minutes slows down because of the square root dependence on time.
- So, cloud drops can grow to 10–20 μm in 15 or so minutes, but then grow bigger much more slowly.
- Since a typical cloud only lasts 10s of minutes, it is not possible for cloud drops to grow into rain drops by vapor deposition alone. For conditions shown in the figure above, it would take 30 days to reach the diameter of a typical rain drop (1000 μm).
- CCN nucleation followed by vapor deposition can make clouds, but it can’t make them rain.
- We can develop a similar expression for vapor deposition on ice, but the vapor depositional growth on ice is a little faster than on liquid.
Conclusion:
We need other processes to get cloud drops big enough to form precipitation, either liquid or solid.