5.8 Did you know most precipitation comes from collision–coalescence?
There are two types of processes for growth into precipitation drops: warm cloud processes and cold cloud processes. In warm clouds, the processes all involve only liquid drops. In cold clouds, the processes can involve only solid particles, as well as mixed phases (both supercooled liquid and ice). Some of the most important processes involve collisions between drops, whether they be liquid or solid.
Collisions
Collisions occur in both cold and warm clouds and can involve either liquid drops or solid particles or both.
- Collision–Coalescence: Large liquid drop scavenges smaller liquid drops as it falls.
- Riming: Falling ice collects liquid water, which freezes on its surface.
- Capture Nucleation: Large liquid drop captures small ice particle, which acts as an ice nucleus and causes the large drop to freeze. The particle that is collected can be either an ice nucleus (IN) or a piece of ice, which also is a good ice nucleus. In either case, the supercooled liquid drop freezes on contact with the IN.
- Aggregation: Falling snowflake scavenges other snowflakes that aggregate to make a larger snowflake bundle.
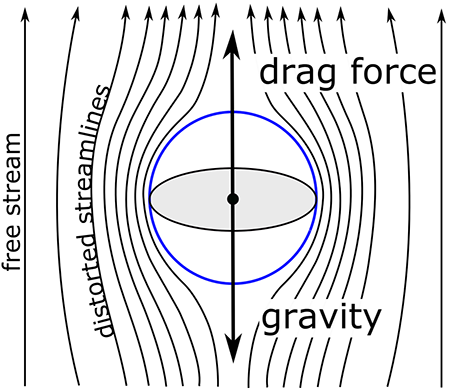
For a cloud drop at rest, gravity is the only external force. Once the cloud drop starts to fall, then the air resistance forms another force called drag, which is a function of the velocity.
In less than a second, the particle reaches a fall speed such that the drag force exactly balances the gravitational force and the velocity becomes constant. This velocity is called the terminal velocity. Because the gravitational force depends on the volume of the drop, it goes as the cube of the drop radius. In contrast, drag acts on the surface of the drop, and so it depends on the drop area and goes as the square of the drop radius (times the velocity). Setting the gravitational and drag forces equal to other and then solving for the terminal velocity, it is easy to show that the terminal velocity should vary linearly with drop radius. Measurements bear this linear relationship out. For instance, the terminal velocity of a 50 μm radius drop is about 0.3 m s–1, while the terminal velocity for a drop 10 times larger (500 μm radius) is about 4 m s–1, which just a little more than a factor-of-10 increase.
The growth of a cloud drop into a precipitation drop by collision–coalescence is given by the equation:
- mL is the mass of the large drop that is falling,
- Ag is the geometric cross-sectional area for which collisions between the falling large drop and the many drops below are possible,
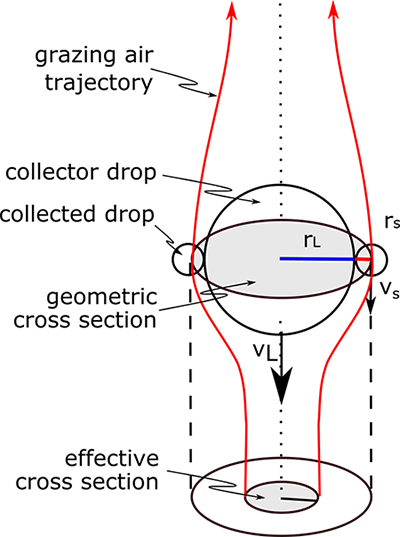
- Ec is the collision–coalescence efficiency (i.e., a collection efficiency), which is the fraction of the actual cross-sectional area that is swept out compared to the cross-sectional area that is geometrically possible (smaller drops can follow air streamlines and go around the big drop) (see the figure below),
- vL is the velocity of the large drop and vs is the velocity of the smaller, slower falling drops below,
- and LWC is the liquid water content.
The figure below provides a good conceptual picture of collision–coalescence. The collector drop must be falling faster than the smaller collected drop so that the two of them can collide. As the air streamlines bow out around the drop, they carry the smaller drops with them around the drop, and the effective cross-sectional area becomes less than the actual cross-sectional area, which is simply the cross-sectional area of a disk with a radius that is the sum of the radii of the large collector drop and the smaller collected drops. As drops get bigger, they have too much inertia to follow the air streamlines, thus making the collision more likely.
Ec is small for 10 μm drops, so by a random process, some drops become bigger than others and begin collecting smaller drops (see figure below). Ec increases as the radius of the falling drop increases. When the larger falling drop gains a radius of more than 100 μm, its collision–coalescence efficiency is very good for all smaller drops down to sizes of about 10–20 μm.
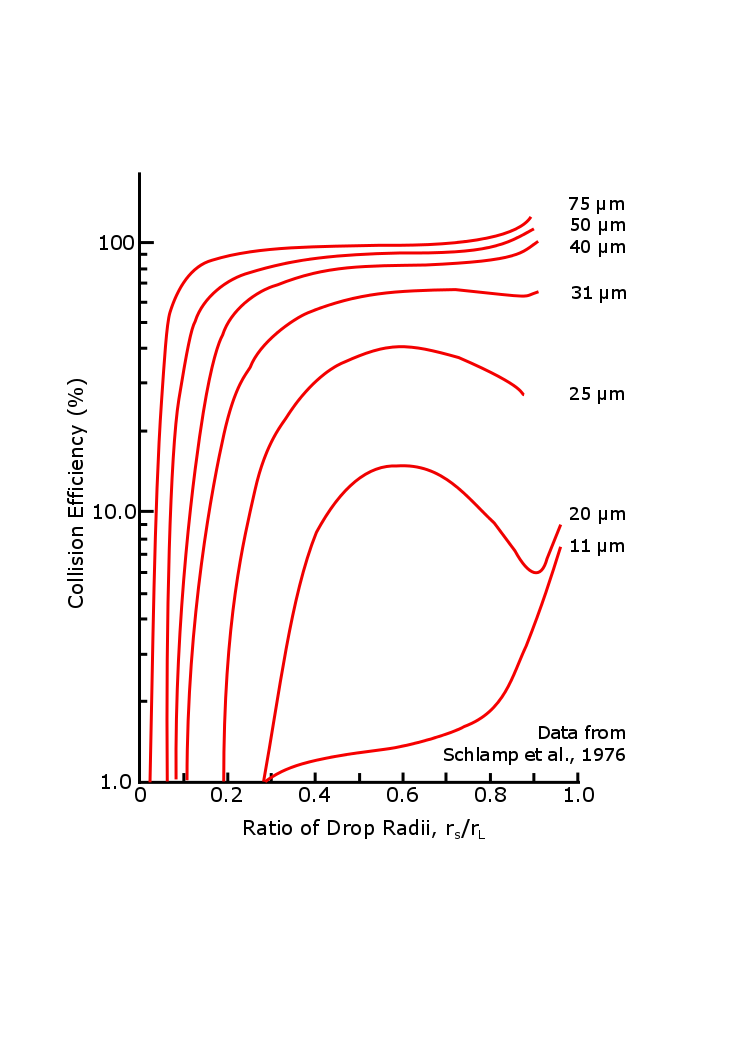
Once a collecting drop has reached a radius of a few hundred μm, it is falling fast (vL >> vs) and its collision–coalescence efficiency is close to 100%. Now take the following steps to rewrite Equation 5.16: (1) Ec equal to 1, (2) vL >> vs, (3) vL = constant x rL, (4) mL = 4ρlπrL3/3 , and (5) solve for drL/dt. Once you take these steps, you can show that drL/dt is proportional to rL. That is, the bigger the drop gets the faster it grows. Separating variables (rL and t) and integrating from rL = 0 at t = 0 to arbitrary values of rL and t reveals that rL increases exponentially with time:
With the constant of proportionality between the terminal velocity and drop radius set at 8 x 103 s–1 and LWC = 1 g m–3, it can be shown that a drop can grow from 50 μm to 1000 μm by collision–coalescence in only 25 minutes. So, the activated cloud drops grow to 10–20 μm by the slow growth of vapor deposition (square root of time). Then when collision–coalescence starts and produces a few big drops, they can grow exponentially with time.
Smaller drops are typically spherical. Once these drops get to be above a mm in radius, they become increasingly distorted, with a flattened bottom due to drag forces, and they look a little like the top half of a hamburger bun. They can be further distorted so that the middle of the bun-shape gets pushed up by the drag forces so that the drop takes on a shape resembling an upside down bowl.
Eventually the drops break up, either by getting thin enough in the middle that they break into pieces or by colliding with other drops so hard that filaments or sheets of liquid break off to form other drops. These processes create a whole range of sizes of drops. Thus rain consists of drops that have a wide spectrum of sizes. The following video (2:50) entitled "How Raindrops are Formed" starts with a simplified view of the atmosphere's water cycle, but then shows examples of a falling drop, collision–coalescence, and cloud-drop breakup.
Now this is a familiar scene. The sun's heat causes water from plants, lakes, and oceans to turn from a liquid to a vapor. High in the atmosphere the water vapor then cools down and condenses from a gas back into a liquid. The liquid water then falls back to the surface in the form of rain, snow, ice, or hail. Water runs off into streams lakes and oceans or is stored in the ground or in snow path. This is the water cycle and it describes our most vital resource moves through the whole earth system, but like most things in our world when we look at the tiny parts that make up the whole we can learn a lot more about the phenomenon. Take the shape of a single raindrop. Small droplets of water in the atmosphere are spherical in shape due to the surface tension or skin of the water molecules. As these droplets grow they become heavier and start to fall through the air. As they fall, the raindrop collides with other drops and continues to get bigger. These larger raindrops fall through the air faster the wind resistance on the underside of the drop causes the bottom of the drop to flatten resulting in a drop looking like a hamburger bun. As the drop continues to fall and grow at some point it becomes too large for the surface tension to hold it together, so the raindrop breaks apart into smaller spiracle drops. Investigating the processes we can't see with the naked eye is nothing new. Science and technology drive each other forward and often lead to insights and discoveries along the way. With the invention of high-speed photography we finally saw the most basic elements of our watery planet in action. Understanding how a tiny raindrop falls through the atmosphere does more than debunk the myth that a raindrop Falls like a teardrop. It actually makes a difference when it comes to measuring precipitation in particular for ground radars. Ground radars look at the sides of the raindrops and then estimate the vertical and horizontal sighs. A heavier, flatter drop allows radars to identify heavier precipitation. In fact the two radars on board the GPM satellite can also measure drop sizes from space and so a more accurate look at rain drops gives us a more accurate look at how global rainfall is shaping up.
For riming, capture nucleation, and aggregation, there are similar equations with terms similar to those in Equation 5.16—an area swept out, a collection efficiency, the relative velocity, and the liquid or solid mass concentration of the smaller drops or ice. These are typically a bit more complicated if the ice is not spherical, but the concepts are the same. These ice collision–coalescence processes are able to produce ice particles big enough to fall, and if these particles warm as they pass through the warm part of the cloud, they can turn into liquid rain. A significant fraction of rain in the summer can come from ice collision–coalescence processes above the freezing line in the clouds.