5.6 Koehler Theory

So, now we can put the pieces together. The equilibrium vapor pressure for a water drop containing a solute is simply the triple product of the saturation vapor pressure for pure water over a plane surface, the curvature effect, and the solute effect:

$\begin{matrix} e_{e q} (n_{s}, r, T) = e_{s} (T) \cdot (1 - χ_{s}) \cdot exp (\frac{2 σ}{n_{L} \cdot R * \cdot T \cdot r_{d}}) \\ \approx e_{s} (T) \cdot (1 - \frac{B i N_{s}}{r_{d}^{3}}) \cdot (1 + \frac{a_{K}}{r_{d}}) \\ = e_{s} (T) \cdot (1 + \frac{a_{K}}{r_{d}} - \frac{B i N_{s}}{r_{d}^{3}} - \frac{a_{K} B i N_{s}}{r_{d}^{4}}) \\ e_{e q} (n_{s}, r, T) \approx e_{s} (T) \cdot (1 + \frac{a_{K}}{r_{d}} - \frac{B i N_{s}}{r_{d}^{3}}) \end{matrix}$

[5.12]

This equation is called the Koehler Equation. It gives us the equilibrium vapor pressure that a drop will have for a given drop radius r_d and given number of moles of solute N_s. We can see that there are two competing effects: the curvature or Kelvin effect that depends on the inverse of the drop radius, and the solute or Raoult effect that depends on the inverse of the drop radius cubed.

Remember we talked about the saturation ratio, S = e/e_s. We also talked about supersaturation, s = S – 1= e/e_s – 1. We define a new saturation ratio and supersaturation for a particle, S_k and s_k, where “k” stands for “Koehler.”

s_k is defined as follows:

$\begin{array}{l} S_{k} = \frac{e_{e q} (n_{s}, r, T)}{e_{s} (T)} \approx (1 + \frac{a_{K}}{r_{d}} - \frac{B i N_{s}}{r_{d}^{3}}) \\ s_{k} = S_{k} - 1 = \frac{a_{K}}{r_{d}} - \frac{B i N_{s}}{r_{d}^{3}} \end{array}$

[5.13]

where

a_{K} = \frac{2 σ}{n_{L} \cdot R * \cdot T}

and

B = \frac{3}{4 π n_{L}}

Equation 5.13 is the form of the Koehler Equation that is most often used. Remember, this equation applies to individual drops. Each drop has its own Koehler curve because each drop has its own amount of solute of a given chemical composition. No two Koehler curves are alike, just as no two snowflakes are alike.

Let's look at a graph of this equation. At 20 ^oC, a_K = 1.1 x 10^–9 m, B = 4.3 x 10^–6 m³ mole^–1, and N_s is typically in the range of 10^–18 to 10^–15 moles.

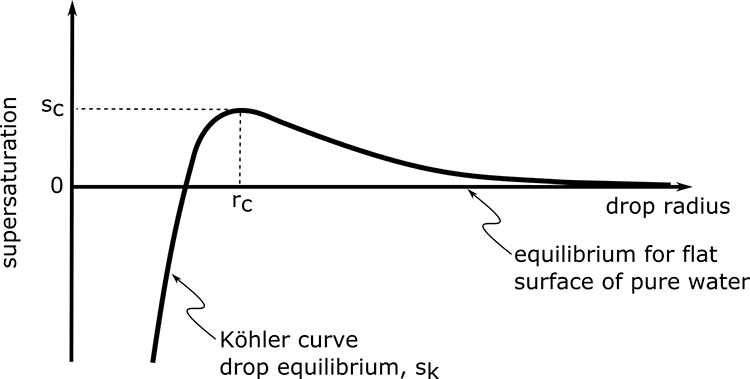
Koehler curve, which is the supersaturation of a particle as a function of the particle radius. The radius increases as the particle takes on water.

Credit: W. Brune © Penn State is licensed under Penn State is licensed under CC BY-NC-SA 4.0

Interpretation of the figure:

s_k is the supersaturation of the particle, not the atmosphere.
At the smallest r_d (~10s of nm), the Raoult solute effect (–1/r_d³) is stronger than the Kelvin effect.
As r_d gets bigger as water is added to the particle, the Kelvin effect (+1/r_d) starts to win out over the solute term (–1/r_d³). As a result, s_k becomes positive.
As r_d gets very large, then the surface begins to look “flat” and the solution becomes so dilute that the liquid water approaches “pure” and s_k approaches 0, which means that e_eq approaches e_s.
s_c is called critical supersaturation. The particle cannot activate and grow into a cloud drop until the atmospheric supersaturation, s, exceeds s_c.
s_c occurs at the critical radius r_c, for activation. Drops that reach this radius can activate and grow into a cloud drop. Those that don’t won’t.
The greater N_s, the lower s_c, and the greater r_c (see next figure).

The video below (1:35) explains the Koehler Curve Equation in more depth:

Koehler Curve Equation

Credit: W. Brune © Penn State is licensed under CC BY-NC-SA 4.0

Click here for a transcript of the Koehler Curve Equation video.

Koehler theory is at the heart of cloud microphysics. It deals with two competing processes. One raises the equilibrium saturation vapor pressure above the [INAUDIBLE] saturation vapor pressure of the flat surface of your water. This is called the Kelvin effect, or the curvature effect. And the second process lowers the equilibrium vapor pressure. This is called Raoult's Law or the solute effect. Review the previous two sections of this lesson if you've forgotten these two effects. We can approximate the curvature effect as a constant over the drop radius and we can approximate the solute effect as the negative a constant over the drop radius cubed. Together they give us supersaturation for a drop. How do these two give us the Koehler curve? The curvature effect goes as a positive inverse of the radius. But the solute effect goes as the inverse of the radius cubed is negative. And at small r it is greater negative than the curvature effect is positive. As a drop gets bigger, then the curvature effect becomes more important. And then the drop equilibrium supersaturation follows the curvature effect. Note that each drop has its own Koehler curve. Supersaturation of the environment, which can be positive by radiative heating, cooling, mixing, [INAUDIBLE] descent, determines what will happen to the drop.

Check Your Understanding

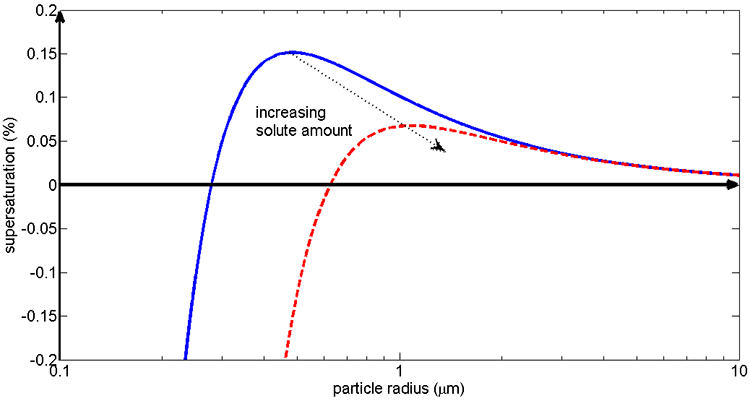
same graph as above, larger # of moles of solute is a shorter peak and a more linear decrease

Koehler curve for two drops: N_s = 1 x 10^–17 moles (blue solid line), N_s = 5 x 10^–17 moles (red dashed line).

Credit: W. Brune © Penn State is licensed under CC BY-NC-SA 4.0

Note that the supersaturation is less than 0.2% for the smaller particle and less than 0.1% for the larger particle. As cooling occurs, which one will activate first?

Click for the answer.

ANSWER: The larger particle, because it has a lower critical supersaturation.

To see what happens to the drop in the atmosphere, we need to compare the Koehler curve for each drop to the ambient supersaturation of the environment. The Koehler curve is the equilibrium supersaturation, s_k, for each drop and it varies as a function of the drop size. The ambient supersaturation, s, is the amount of water vapor available in the environment. When s_k = s, the drop is in equilibrium with the environment. The drop will always try to achieve this equilibrium condition by growing (condensing ambient water vapor) or shrinking (evaporating water) until it reaches the size at which s_k = s if it can! Another way to think about s_k is that it is telling us something about the evaporation rate for each drop size and temperature. For the drop to be in equilibrium with the environment, the condensation rate of atmospheric water vapor must equal the evaporation rate of the drop. If s_k < s, then net condensation will occur and the drop will grow. If s_k > s, then net evaporation will occur and the drop will shrink.

Let's look at two cases. In the first case, the ambient supersaturation is always greater than the entire Koehler curve for a drop.

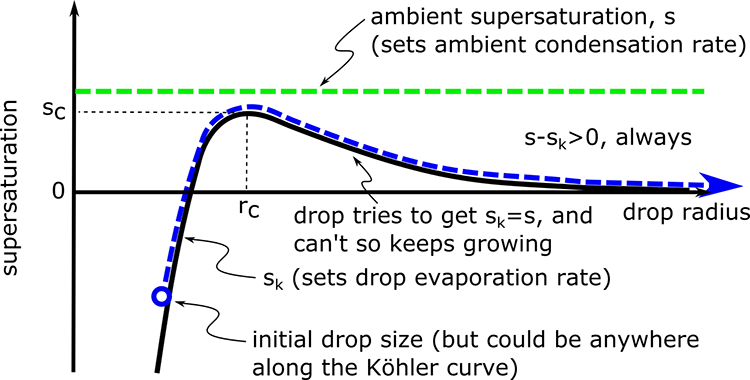
see text below for interpretation. Graph is same curve as above, ambient supersaturation is above (rc,sc) point

Koehler curve for a drop in an environment where the ambient supersaturation is greater than the entire Koehler curve.

Interpretation of the figure:

The ambient supersaturation does not depend on the radius of the particle and so is a straight line on the graph.
The basic concept is the particle supersaturation is constrained to the s_k curve, the particle grows or shrinks in an effort to have s_k = s, that is, to have the particle condensation and evaporation be in equilibrium with the environment’s water vapor.
If s > s_c, then the condensation of ambient water vapor is greater than the evaporation from the drop no matter what the drop radius is.
The particle continues to grow, becomes a critical nucleus, and then continues to add water and grow into a cloud drop.
The drop can start at any size and it will grow into a cloud drop as long as the ambient supersaturation is greater than the Koehler curve.

In the second case, the ambient supersaturation intersects the Koehler curve:

see text below for interpretation. Graph is same curve as above, ambient supersaturation is below (rc,sc) point and intersects the curve 2x

Koehler curve for a drop in an environment where the ambient supersaturation intersects the Koehler curve.

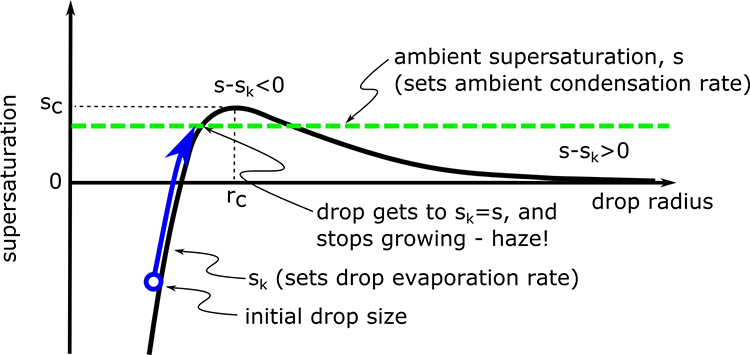
Interpretation of the figure:

If s < s_c and the drop radius is very small, then the drop grows to a radius on the left side of s_c and stops when s_k = s.
The drops are called haze drops. They do not nucleate to become cloud drops but instead stay a smaller size. You have probably often seen haze on a warm, moist summer day.
If a drop finds itself in an environment where s < s_k, (as could happen if the drop's air is mixed with drier air), then the evaporation from the drop would exceed the condensation from the environment and the drop would shrink until s = s_k.
If a drop happens to find itself in an environment where s = s_k, the drop can shrink back into a haze drop or grow into a cloud drop, depending on the drop radius. If r < r_c, then the drop will shrink until it has a radius for which s = s_k. If r > r_c and s = s_k, then the drop is in unstable equilibrium and can either grow into cloud drops by adding a water molecule or can shrink all the way back to a haze drop with a radius that matches the radius for s = s_k.
If s = s_c (which is a special case of s = s_k) then the drop will grow to radius r = r_c and then with the random addition of a little water will grow a little bit more so that s_k < s. At this point, there will be net condensation and the drop will activate and continue to grow.

You can imagine all kinds of scenarios that can happen when there is a distribution of cloud condensation nuclei of different sizes and different amounts of solute. Drops with more solute have lower values for the critical supersaturation and therefore are likely to nucleate first because, in an updraft, the lower supersaturation is achieved before the greater supersaturation. So you can imagine the larger CCN taking up the water first and taking up so much water that the ambient supersaturation drops below the critical supersaturation for the smaller CCN. As a result, the larger CCN nucleate cloud drops while the smaller CCN turns into haze. The moral of the story? If you're a CCN, bigger is better!

Quiz 5-3: How cloud drops form.

Find Practice Quiz 5-3 in Canvas. You may complete this practice quiz as many times as you want. It is not graded, but it allows you to check your level of preparedness before taking the graded quiz.
When you feel you are ready, take Quiz 5-3. You will be allowed to take this quiz only once. Good luck!

5.6 Koehler Theory