Trilateration is an alternative to triangulation that relies upon distance measurements only. Electronic distance measurement technologies make trilateration a cost-effective positioning technique for control surveys. Not only is it used by land surveyors, trilateration is also used to determine location coordinates with Global Positioning System satellites and receivers.
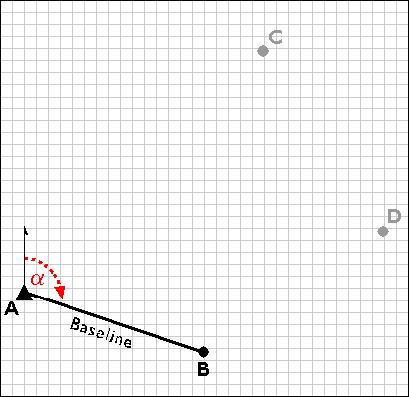
Trilateration networks commence the same way as triangulation nets. If only one existing control point is available, a second point (B) is established by open traverse. Using a total station equipped with an electronic distance measurement device, the survey team measures the azimuth α and baseline distance AB. The total station operator may set up her instrument over point A, while her assistant holds a reflector mounted on a shoulder-high pole as steadily as he can over point B. Depending on the requirements of the control survey, the accuracy of the calculated position B may be confirmed by astronomical observation.
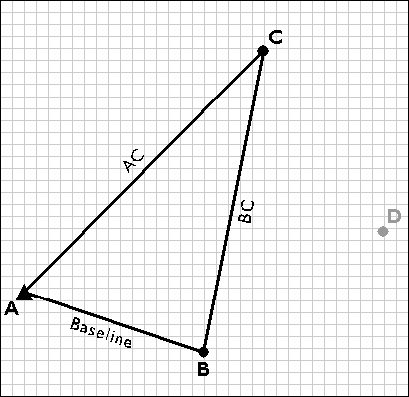
Next, the survey team uses the electronic distance measurement feature of the total station to measure the distances AC and BC. Both forward and backward measurements are taken. After the measurements are reduced from slope distances to horizontal distances, the law of cosines can be employed to calculate interior angles, and the coordinates of position C can be fixed. The accuracy of the fix is then checked by plotting triangle ABC and evaluating the error of closure.
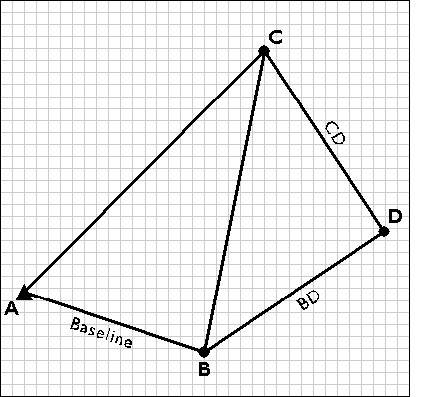
Next, the trilateration network is extended by measuring the distances CD and BD, and fixing point D in a plane coordinate system.