Effect of Composition on Phase Behavior

Let us try to reconcile the P-T graphs for the binary mixture with what we know from P-T graphs for single-component systems. At the end of the day, a mixture is formed by individual components which, when pure, act as presented in the P-T diagram shown in Fig. 3.1 [Module 3, repeated below]. We would, therefore, expect that the P-T diagram of each pure component will have some sort of influence on the P-T diagram of any mixture in which it is found.

Figure 3.1 (repeated): Vapor pressure curve

In fact, it would be reasonable to think that as the presence of a given component A dominates over B, the P-T graph of that mixture (A+B) should get closer and closer to that of A as a pure component.

What this is telling us is that a new variable is coming into the picture: composition. So far we have not considered the ratio of component A to component B in the system. Now we are going to study how different ratios (compositions) will give different envelopes, i.e., different P-T behaviors.

Let us say that we have a mixture of components A (Methane, CH₄) and B (Ethane, C₂H₆), where A is the more volatile of the two. It is clear that for the two pure components, we would have two boiling point curves for each component (A and B) as shown in Figure 5.1.

Figure 5.1: P-T Graphs For The Pure Components A And B

(Bloomer, O.T., Gami, D.C., Parent, J.D., “Physical-Chemical Properties of Methane-Ethane Mixtures”. Copyright 1953, Institute of Gas Technology (now “Gas Technology Institute”, in Chicago). Research Bulletin No. 17.)

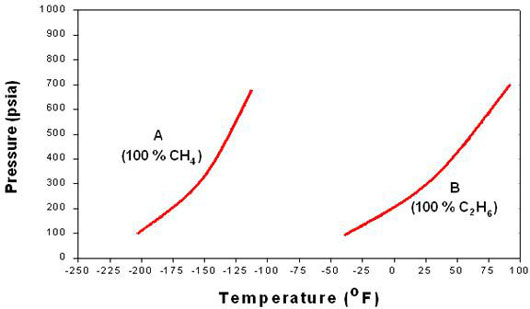
Please notice that the position of each of curve with respect to the other depends on its volatility. Since we are considering A to be the more volatile, it is expected to have higher vapor pressures at lower temperatures, thus, its curve is located towards the left. For B, the less volatile component, we have a boiling point curve with lower vapor pressures at higher temperatures. Hence, the boiling point curve of B is found towards the right at lower pressures.

Now, if we mix A and B, the new phase envelope can be anywhere within curves A and B. This is shown in Figure 5.2, where the effect of composition on phase behavior of the binary mixture Methane/Ethane is illustrated.

Figure 5.2: Effect Of Composition On Phase Behavior.

(Bloomer, O.T., Gami, D.C., Parent, J.D., “Physical-Chemical Properties of Methane-Ethane Mixtures”. Copyright 1953, Institute of Gas Technology (now “Gas Technology Institute”, in Chicago). Research Bulletin No. 17.)

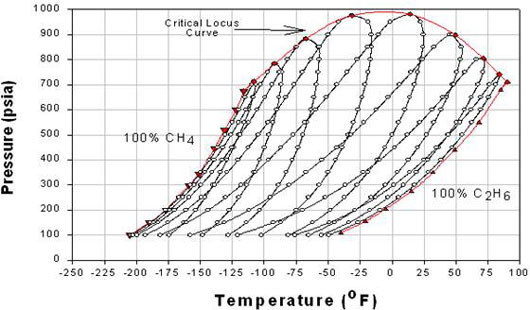
In Figure 5.2, each phase envelope represents a different composition or a particular composition between A and B (pure conditions). The phase envelopes are bounded by the pure-component vapor pressure curve for component A (Methane) on the left, that for component B (Ethane) on the right, and the critical locus (i.e., the curve connecting the critical points for the individual phase envelopes) on the top. Note that when one of the components is dominant, the curves are characteristic of relatively narrow-boiling systems, whereas the curves for which the components are present in comparable amounts constitute relatively wide-boiling systems.

Notice that the range of temperature of the critical point locus is bounded by the critical temperature of the pure components for binary mixtures. Therefore, no binary mixture has a critical temperature either below the lightest component’s critical temperature or above the heaviest component’s critical temperature. However, this is true only for critical temperatures; but not for critical pressures. A mixture’s critical pressure can be found to be higher than the critical pressures of both pure components — hence, we see a concave shape for the critical locus. In general, the more dissimilar the two substances, the farther the upward reach of the critical locus. When the substances making up the mixture are similar in molecular complexity, the shape of the critical locus flattens down.