The next more complex type of multi-component system is a ternary, or three-component, system. Ternary systems are more frequently encountered in practice than binary systems. For example, air is often approximated as being composed of nitrogen, oxygen, and argon, while dry natural gas can be rather crudely approximated as being composed of methane, nitrogen and carbon dioxide. We can also have pseudo 3-component systems, which consist of multicomponent systems (more than 3 components) that can be described by lumping all components into 3 groups, or pseudo-components. In this case, each group is treated as a single component. For example, in CO2 injection into an oil reservoir, CO2, C1, and C2 are often lumped into a single light pseudo-component, while C3 to C6 form the intermediate pseudo-component, and the others (C8+) are lumped together into a single heavy pseudo-component.
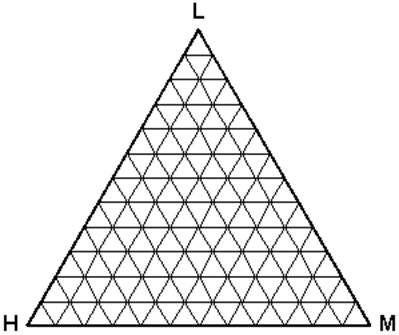
Intuitively, having more than two components poses a problem when a pictorial representation is desired. A rectangular coordinate plot, having only two axes, will no longer suffice. Gibbs first proposed the use of a triangular coordinate system. In modern times, we use an equilateral triangle for such a representation. Figure 5.6 shows an example of a ternary phase diagram. Note that the relationship among the concentrations of the components is more complex than that of binary systems.
Features:
- Any point within this triangle represents the overall composition of a ternary system at a fixed temperature and pressure.
- By convention, the lightest component (L) is located at the apex or top of the triangle. The heavy (H) and medium (M) components are placed at the left hand corner and right hand corner, respectively.
- Every corner represents a pure condition. Hence, at the top we have 100 % L, and at each side, 100 % H and 100 % M, respectively.
- Each side of the triangle represents all possible binary combinations of the three components.
- On any of those sides, the fraction of the third component is zero (0%).
- As you move from one side (0 %) to the 100 % or pure condition, the composition of the given component is increasing gradually and proportionally. At the very center of the triangle, we find 33.33 % of each of the component.
To differentiate within the two-phase region and single-phase region in the ternary diagram, pressure and temperature must be fixed. There will be different envelopes (binodal curves) at different pressures and temperatures. The binodal curve is the boundary between the 2-phase condition and the single-phase condition. Inside the binodal curve or phase envelope, the two-phase condition prevails. If we follow the convention given above (lights at the top, heavies and mediums at the sides), the two-phase region will be found at the top. This can be seen more clearly in Figure 5.7.
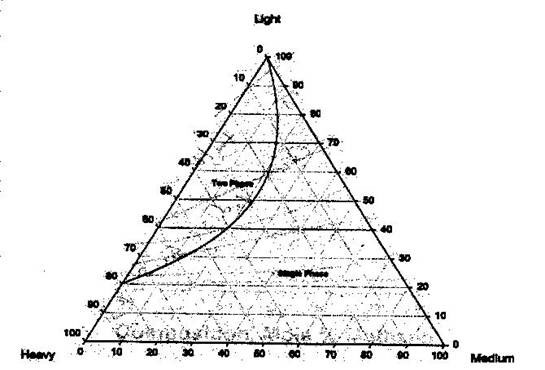
The binodal curve is formed of the bubble point curve and the dew point curve, both of which meet at the plait point. This is the point at which the liquid and vapor composition are identical (resembles the critical point that we studied before). Within the two-phase region, the tie lines are straight lines that connect the compositions of the vapor and liquid phase in equilibrium (bubble point to the dew point). These tie lines angle towards the medium-component corner. It can also be recognized that any mixture on a tie line has the same liquid and vapor compositions.
Finally, to find the proportion of liquid and vapor at any point on the tie line, we apply the lever rule.