Stellar Velocities

Additional reading from www.astronomynotes.com

• Doppler effect
• The Velocities of stars

In the section on parallax, I discussed how the apparent back and forth motion of nearby stars allows us to determine their distances. Besides this apparent motion, can we detect the motion of stars through space? The answer is yes, and we can measure their velocities with different techniques. For any velocity, you can always break it up into components along two perpendicular axes. In astronomical terminology, we do the following: The total velocity of a star includes some motion along our line of sight,—that is, either towards or away from us (called the radial velocity)—and some motion across the sky, perpendicular to the radial velocity. This second component is called the proper motion, and it is actually the more difficult measurement to make.

If you take several images of a star field over time, most of the stars visible in the frame will be in the same place in each frame down to the limit of your ability to measure their location. However, some nearby stars can move noticeably, similar to Barnard's star in the movie at the link above. Barnard’s star moves by a distance equal to the diameter of the Moon (about half a degree) in 180 years. For most stars, which are more distant from us than Barnard’s star, the proper motion is much smaller. A typical value of the proper motion for a star is only a few thousandths of an arcsecond each year. Thus, it can take a 50-year time difference between photographs for a typical star to move by an easily measurable amount so that its proper motion can be determined with reasonable precision.

On the other hand, the radial velocity (motion towards or away from us) can be measured from one observation of a star’s spectrum! This is because the absorption lines in the spectrum of a star shift because of the Doppler Effect.

Figure 4.7: The Doppler Effect—Waves emitted by a source moving from the right to the left. The frequency is higher on the left (ahead of the source) than on the right.

Credit: Wikipedia

The waves of light in the figure are represented as rings, similar to the waves in a pond. If the source of a wave is stationary, the space between each ring (the wavelength) should be constant, and the rings should appear completely circular. An observer located anywhere around the source will record the wave arriving at her location with a wavelength equal to the wavelength as it was emitted.

If the source of a wave is moving as in the image above, the space between each ring is getting smaller in the direction of motion, because the source is "catching up" to the waves it emitted previously. On the opposite side of the ring, the space between the rings has increased. So an observer in front of the moving source will measure a smaller wavelength than the emitted wavelength, and an observer behind the moving source will measure a larger wavelength than the emitted wavelength. Note, however, that in the example above, the observer located above or below the moving source will still measure the emitted wavelength, because the only change in the wavelength occurs for observers who observe the source’s motion along their line of sight. For an animation of this effect, see:

• ExploreLearning: Doppler Effect
• Java Applet: Doppler Effect

Because optical light with a short wavelength is blue, and long wavelength light is red, when the wavelength of light gets shortened by the Doppler effect, we refer to the change in the wavelength as a Blueshift. When the wavelength of light gets lengthened by the Doppler shift, we refer to the change as a Redshift.

Two additional notes:

1. It doesn't matter if the source is moving or the observer is moving. That is, if the source of the waves is stationary, but you are approaching it, you will see a blueshift.
2. The change in the wavelength is proportional to the apparent velocity of the source. That is, the faster the source is moving, the more of a shift you will see.

Recall that light can be interpreted to behave like a wave. So, if you have a moving source of light, then the light it emits will experience the Doppler effect, too. Here is an example:

Fig. 4.8: The spectrum from a stationary source on the left, and on the right, the spectrum from the same source with its absorption lines redshifted because of the Doppler Effect.

Credit: Wikimedia Commons

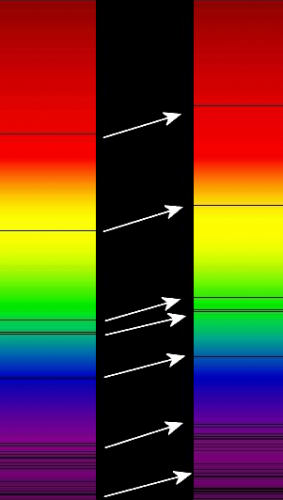
In practice, astronomers compare the wavelength of absorption lines in the spectrum of a star to the wavelength measured for the same lines produced in the laboratory (for example, the Balmer series lines of hydrogen). The following formula is then used to derive the radial velocity of the star:

$\Delta \lambda /{\lambda }_0 =v_r /c$

In this equation, $\Delta \lambda$ is the difference between the measured wavelength of the line in the star’s spectrum and its wavelength in the lab. The rest wavelength is ${\lambda }_0$ , which is the wavelength of the spectral line as measured in the lab. The radial velocity of the star is $v_r$ , and $c$ is the speed of light.

For example, the rest wavelength of the first Balmer line of hydrogen (usually referred to as $Hydrogen-\alpha ,orjustH\alpha$ ) is $656.3nanometers$ . If we measure the $H\alpha$ in a star to have a wavelength of 657.0 nm, then its radial velocity is:

$\Delta \lambda /{\lambda }_0 =\left(657.0–656.3\right)/656.3=0.001$

$v_{r }/c=0.001$

$v_r =cx0.001=3.0x{10}^5 km/secx0.001=300km/sec$

Since the sign of the velocity is positive, this means that the object is moving at 300 km/sec away from the observer.

This is a very common technique used to measure the radial component of the velocity of distant astronomical objects. The steps are to

1. take the object's spectrum,
2. measure the wavelengths of several of the absorption lines in its spectrum, and
3. use the Doppler shift formula above to calculate its velocity.

Note that this requires you to know the rest wavelength of the line as measured in the laboratory, which means you need to be able to identify the line in the spectrum of the object even if it has been shifted far from its rest wavelength. This is one of the difficult tasks of observational astronomy.