Market Power and Monopoly

Our first assumption is that of market power, which states that everybody is a price taker, or that there are many buyers and sellers in a market. In this case, the equilibrium price in a market is defined by so many different transactions that anybody who wishes to buy or sell in this market has to do so at the market equilibrium price, and they are not able to move the equilibrium price with their own actions. Hence, you have to "take" whatever the price is. If you are able to move the equilibrium price with your own choices, then you can be referred to as a "price-setter." In reality, in many situations, somebody in the market has some power to change prices through their individual actions. These include:

• Monopoly: only 1 seller.
• Duopoly: 2 sellers.
• Oligopoly: a few sellers.
• Monopsony: only 1 buyer.

Monopoly

This is the most extreme, but not the most common, example of market power. A monopoly is a market with only one seller. A monopolist is free to set prices or production quantities, but not both because he faces a downward-sloping demand curve. He cannot have a high price and a high quantity of sales – if he has a high price, people will buy less.

There are three ways that a monopoly can exist and/or persist:

1. All of some resource is owned by some firm (e.g., deBeers and diamonds).
2. The government allows a monopoly to exist (not common in the US, but in many countries things like airlines or railways are government-designated monopolies).
3. A Natural Monopoly exists (e.g., your local power company). We will talk more about natural monopolies a bit later in the course.

At this point, you might think about some markets that have a dominant market share held by a single firm, such as Microsoft in the market for spreadsheet software. These are not monopolies, in that firms in these markets do have competitors, and consumers do have choices. If a firm obtains an inordinate market share due to offering a product that many people want to buy, we do not have a monopoly. Firms in a case such as this may have a lot of market power, and may face a lot of scrutiny from the government, but they are not technically monopolies.

Why is a monopoly bad?

Monopolies are typically assumed to be undesirable market structures. They are undesirable, or "bad," because in this case "bad” means less than the most possible total wealth – the sum of the producer and consumer surpluses. A market in which there is a monopoly will generate less wealth for a society than a competitive market would.

A monopoly leads to the following:

• A lower quantity of goods produced and consumed than in a competitive market.
• A higher price than the equilibrium price in a competitive market.
• A higher profit for the firm. In a monopoly, a firm will typically make greater than zero economic profit (remember that term?).

In a competitive market, it is the act of competition that drives prices towards the equilibrium price and quantity at which the marginal firm makes zero economic profits - they are earning just enough money to cover their costs of production and to pay their owners a return that is sufficient to cover their risks. If firms in an industry are making positive economic profits, then other firms have an incentive to enter the market to try and deliver these positive profits to their owners. Generally, this extra market entry is enough to increase production and decrease equilibrium price to the point where zero economic profits are seen. In a monopoly, these competitive pressures are absent. A firm is able to earn positive economic profits, and because they are a monopoly, other firms are unable to enter their market and drive down price.

This leads to an increase in the size of the producer surplus and a decrease in the size of the consumer surplus. As a disinterested economist, we might say "who cares?" especially if we are generating wealth. That is, should we care who gets the wealth, as long as wealth is being generated? That would be a "normative" statement. However, since we are concerned with maximizing the aggregate wealth of a society, we can ask the positive question "does a monopoly decrease total wealth generated?" If it does, then we have the definition of a market failure.

It is quite easy to answer this question with a supply and demand diagram. But first, consider how a monopoly works. We may have a single seller, and this seller may be able to choose his price, but he cannot control the demand curve. Remember, the demand curve is defined by the marginal utility of consumption, a measure of how much happiness the consumers get from consuming. So, the monopolist faces a demand curve he or she cannot change. So what a monopolist can do is choose just where the supply curve intersects the demand curve. He can choose any combination of price or quantity that exists along the demand curve. If he picks a high quantity, then he chooses a low price, or vice-versa. He cannot have a high price and high quantity. When I say "high" here, I am speaking in relationship to the competitive market equilibrium.

So, a monopoly producer will typically restrict output to some quantity below the market equilibrium. This is illustrated on the following supply and demand diagram, where $Q_{\mathrm{m}}$ refers to the quantity produced by the monopolist. To find out what price we see in this market, draw the line up from $Q_{\mathrm{m}}$ until it intersects the demand curve. This gives us the monopoly price, $P_{\mathrm{m}}$ . These contrast to the "free-market" equilibrium, which I label as $\mathrm{Q*}$ and $\mathrm{P*}$ in this diagram.

As you can see, since $Q_{\mathrm{m}}$ < $\mathrm{Q*}$ , then $P_{\mathrm{m}}$ has to be greater than $\mathrm{P*}$ , because the demand curve is downward-sloping.

Figure 5.1 Supply and Demand diagram showing DWL

Credit: F. Tayari © Penn State is licensed under CC BY-NC-SA 4.0

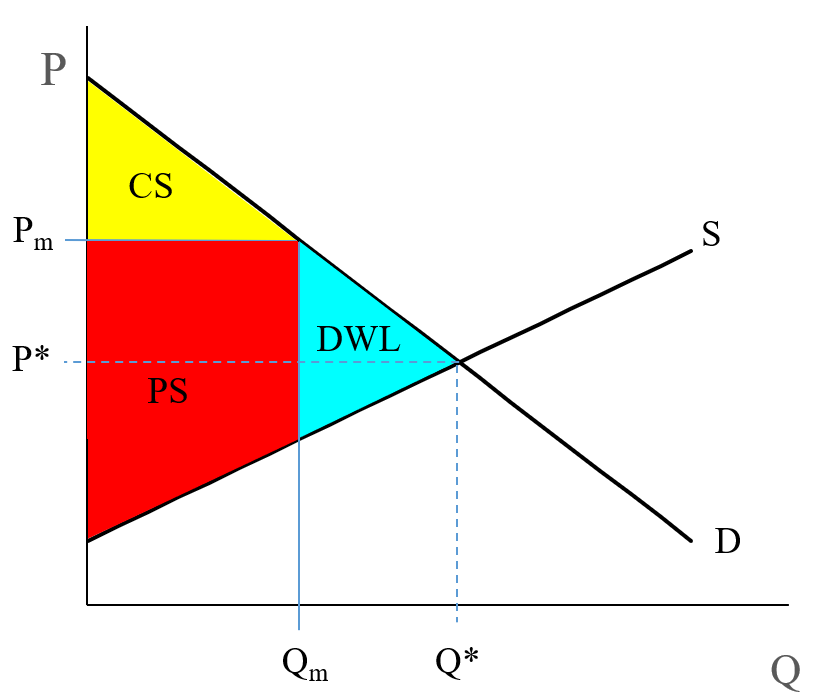
In a competitive market, wealth is the sum of the red, yellow, and blue areas. In the monopoly market, it is just the sum of the yellow and red areas. The blue area is wealth that is lost to society. This area is the Deadweight Loss. This labeled as "DWL" in Figure 5.1. This is the cost to a society of allowing a monopoly to operate. So, in a monopoly, the producer makes more, the consumer makes less, and the society, added together, is poorer as a result.

This is called a Social Cost: a cost to the total society.