PrintAnnual Percentage Rate (APR) is usually used for loans, mortgages, and so on. APR represents an annualized expression of the cost of borrowing money.
When you take out a loan or mortgage on a property, in addition to the interest, you are required to pay some other transaction costs such as points*, loan origination fees, a home inspection fee, mortgage insurance premiums, … . Considering these costs, the amount of money that you will receive is actually somewhat less than what you requested. APR is the expression that reflects some of these costs, and under the Federal Truth in Lending Law, Regulation Z, the lender is required to provide this information to the borrower. Since APR includes mentioned transaction costs, it is higher than interest rates. You can think of APR as the rate of return on the loan taking process considering its costs.
* Loan points are a percentage of the loan value that is deducted as transaction cost.
APR can be a good tool for comparing different loans offered by lenders. But there are two issues that need to be considered before comparing APRs:
- how the lender calculates APR and what costs are included;
- the fact that the difference between APR and loan interest rate is higher for smaller loans with shorter lifetimes, considering similar costs.
For More information about APR please watch the video linked below.
Annual Percentage Rate Video (1:34)
Investopedia presents: Annual Percentage Rate
The annual percentage rate or APR is the cost per year of borrowing. By law, all financial institutions must show customers the APR of a loan or credit card. Which clearly indicates the real cost of the loan. APR is not the same as the interest rate on a loan. Loans charge and interest rate but usually also charge other fees such as closing costs, origination fees, or insurance costs which are typically wrapped into the loan. If two loans have the same interest rate but one has much higher fees than the other, simply shopping by interest rates won’t give an accurate comparison of the loan's true cost. That’s why there is an APR. By factoring in other fees APR gives a more accurate estimate of the cost per year of a loan. For this reason, the APR is generally higher than the interest rate.
For example, a mortgage company may offer a customer an interest rate of 4% on a mortgage loan of $100,000 but after closing costs and other fees, the loan may have an APR of 4.1%. Unfortunately, not all financial institutions include the same fees in their APR calculation, so APRs are not always a perfect comparison tool. When comparing load or credit card APR’s ask what fees are included so your comparison is accurate.
Example 3-1
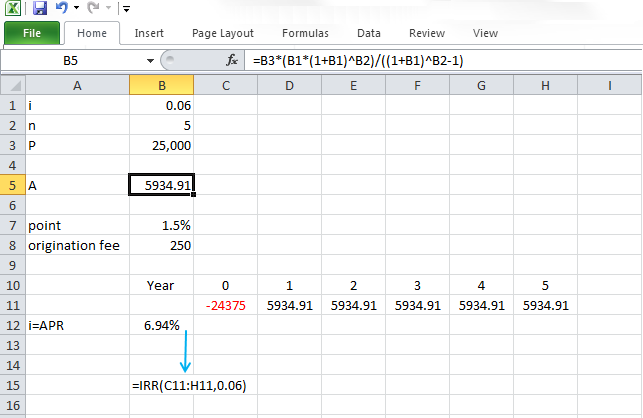
Calculate the APR for a 5-year, $25,000 loan with the interest rate of 6% (compounded annually), considering 1.5 points and loan originating fee of 250 dollars. Assume all the costs are deducted at the time of taking the loan (present time).
Note: 1.5 points equals a cost of 1.5% of the loan value.
First, the uniform series of annual payments needs to be calculated.
Regarding Table 1-12 and Equation 1-6
Then, we have to calculate the costs and deduct them from the loan:
So, borrower will receive $24,375 at the present time and pay $5,934.91 to the bank, each year, starting from end of the year 1:
Now, we have to calculate the rate of return for such a project.
| Loan-cost= 24,375 | A=5,934.91 | A=5,934.91 | A=5,934.91 | A=5,934.91 | A=5,934.91 |
|
|
|||||
| 0 | 1 | 2 | 3 | 4 | 5 |
Present value of loan – present value of the costs = present value of all annual payments
With the trial and error technique, explained in the Lesson 2 section “Break-Even and Rate of Return (ROR) Calculations II,” we can calculate i =6.94% as the APR for loan.
Please watch the following video, Calculating APR for a loan or mortgage (4:43).
PRESENTER: In this video, I'm going to explain how to calculate Annual Percentage Rate, or APR, for loans or mortgages. APR is a parameter that shows the annual cost of borrowing money. When you're going to take out a loan or mortgage on a property, in addition to the interest, you will pay some other transaction costs, which usually includes points, loan origination fees, home inspection fee, mortgage insurance premiums, and closing costs.
So eventually, you will receive a little bit less than the amount that you ask for for the loan or mortgage. APR is the parameter that helps you calculate the true cost of borrowing money. APR reflects some of these costs, but not all of them. So when you take a loan or mortgage, you need to ask what costs are included in the APR.
So APR is very close to the interest rate of the loan or the mortgage, but it will be a little bit higher because you receive a little bit less amount of money. Let's work on this example. Let's assume we're going to take $25,000 of loan at the present time with the interest rate of 6%, compounded annually. And we have to pay off the loan in five years.
And costs are going to be 1.5 points. And loan originating fee of $250. Let's calculate the APR for this loan.
The first thing that needs to be calculated is the uniform series of annual payments that we have to pay each year to pay off the loan. So we can use the factor A over P to calculate this uniform series of annual payments. So $25,000, multiply the factor A over P and the equation, and the result. So we have to pay $5,935 per year for five years to pay off the loan.
In the next step, we have to calculate the loan costs. Here, we have points and loan origination fee. We have 1.5 points, which means the cost is going to be 1.5% of the total original amount of loan $25,000, which comes to $375, and loan origination fee, which is $250. So total cost of the loan is going to be $375 plus $250, which comes to $625.
In the next step, we have to deduct the loan cost of $625 from the original amount of the loan, which was $25,000. We are going to actually get $24,375 at the present time, but we have to pay $5,935 per year. In order to calculate the APR of this project, we need to calculate the return on this project.
Let's say you are going to receive $24,375, and you need to pay $5,935 per year for five years. So in order to calculate the rate of return, we write the equation present value of loan minus present value of cost should be equal to present value of all annual payments. And we calculate the rate of return for this project, which will be 6.94%.
And this is going to be the APR of the loan. Please note that APR should be very close to the interest rate. As we can see here, the APR of 6.94% is very close to the loan interest rate of 6%.
Excel formula to calculate Rate of Return
Rate of return for an investment can be determined by the try and error method that is previously explained. Also, a convenient way to learn to calculate rate of return is to use Microsoft Excel or Google Sheets and apply Internal a Rate of Return (IRR) function to the cash flow.
Note: You have to enter the occurred amounts in the spreadsheet in the form of cash flow (you can enter the years in horizontal or vertical direction). It means inflow and outflow of cash should be entered with different signs (depending on the project). So, you can enter the loan with negative signs at the present time and annual payments in following years with positive signs.
More information about the IRR function in provided in following links.
IRR Function in Microsoft Excel
Please watch the following video, Internal Rate of Return (1:58).
The IRR function calculates the internal rate of return of a series of cash flows. In this example, we have a series of cash flows, starting with an initial investment, a negative number in Period 0, and then a whole bunch of cash inflows over the next five years. We'd like to work out what the internal rate of return of these cash flows are.
If we click in the cell where we want the result, we can activate the Function Wizard. We can go to the Financial category, go to IRR. And when we say OK, we are asked for these arguments.
The first one is the values, which is basically an array or reference to cells that contain the numbers for which we want to calculate the IRR. So in that case, it would be this list here. And then you are asked for a guess. And in some cases, the IRR cannot come up with a number. You need to put in a guess. And generally, I'll put in 0.1, or 10%. And when you click OK, you'll see that the IRR is calculated.
In order for the IRR to work, you need to understand two issues. The first is that your series of cash flows must contain at least one negative number and at least one positive number in order for it to work, otherwise it'll deliver an error message.
The second issue is that unlike the NPV function, the IRR function assumes that the first value it is given occurs in Period 0, and after that it goes to Period 1, 2, whereas the NPV function assumes that the first number it's given occurs at the end of Period 1. This is extremely important, especially if you're trying to reconcile your NPVs to your IRR numbers.
Figure 3-1 displays the APR calculations for Example 3-1.
