4.1 The Concept of Procedural Modeling

4.1 The Concept of Procedural Modeling

As discussed in Module 2, procedural modeling is about constructing detailed textured 3D models by formulating rules instead of manually modeling them (CityEngine). These rules are constructed based on a specific type of shape grammar (Stiny & Gips 1971). Stiny and Gips invented shape grammars and defined shape grammars as a method of two and three-dimensional shape generation. A shape grammar is a set of shape transformation rules to generate a language or set of design (Knight, 1989; Duarte & Beirao, 2010). They are spatial rather than symbolic and also non-deterministic. It means that the designer is not constrained by a limited choice of rules (Knight, 1989).

Shape Grammar is a way of defining algorithms. It makes design, generally speaking, more understandable. In order to read and use shape grammars, we need to have a short review of the basic terms below (Stingy, 1980):

• Grammar: A set of rules of transformation.
• Language: A set of all the possible designs can be generated with the grammar rules.
• Shapes: points, lines, planes, or volumes.
• Labels: symbols, numbers or words that restrict the rules that apply.
• Initial Shape: The first labeled shape that the rules are applied to.
• Rule: A process transfer shapes and label from the left side to the right side (α-->β).
• Transformation: Usually is Euclidean transformations, changing location, orientation, reflection, or scale of a shape.
• Derivation: apply the rules to the initial shape recursively and generate new shapes.

A shape rule specifies how the existing part of a shape can be transformed. It consists of two labeled shapes on each side of the arrow (α-->β). Each labeled shape is made up of a finite set of shapes which are points, lines, planes, or volumes. For instance, in the figure below a simple shape grammar consisting of two rules is defined. The first rule specifies that a triangle with a dot can be modified by adding an inscribed triangle and removing the dot from the original triangle. The second rule states that one can also simply remove the dot from a triangle with a dot. Given the initial shape of a triangle with a dot, a shape can be derived by applying these two shape rules in a different order, namely, rule a -> rule a -> rule b in this case.

Figure: Shape Grammar

Credit: ChoroPhronesis Lab

To create an urban plan or design, the complexity and characteristics of that environment can be interpreted as shape grammars to increase flexibility in suggesting the number of solutions and scenarios. Duarte & Beirao (2010) indicate that old urban plans are not compatible with contemporary urban societies and that there is a need for flexible designs. They propose that there are two ways to use shape grammars in urban environments: (1) as an analytical tool to find the structure of an existing design, or (2) as a synthetic tool to create a new language for design. Both methods automate the process of design generation.

Although a shape grammar can be generated by hand, for more complex rules and choices, a generation engine is needed to create and display geometries and decide which shape rule to apply. ESRI CityEngine is a generation engine for creating shape grammars, applying rules, and generating shapes. CityEngine’s programming language to define shape rules is called CGA (computer-generated architecture) shape grammar. The next section briefly explains the CGA shape grammar and how it can be applied to create virtual 3D models of cities.

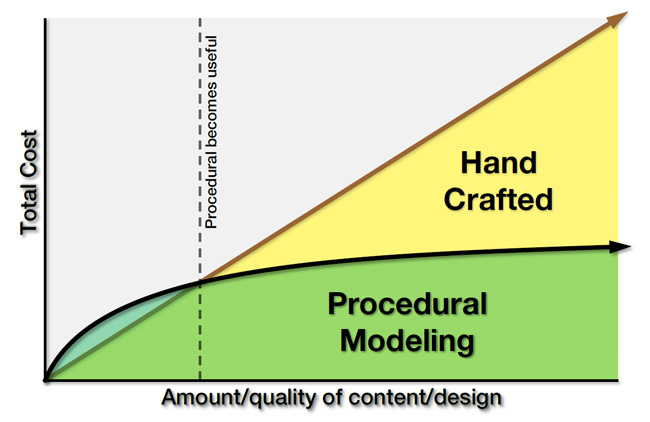
Creating a model based on rules is less labor-intensive. However, the preparation of rules is time-consuming. The strength of this modeling approach is that once the rules are created, generating and creating models takes a small amount of time. The following diagram shows the total cost of procedural modeling vs handcrafted modeling.

Figure: Total cost of procedural modeling VS handcrafted modeling

Credit: CityEngine