Additional reading from www.astronomynotes.com
To begin this page, let me ask a rhetorical question:
How close to you must a car be in order for you to tell that it has two headlights?
On the page, there is no opportunity for me to pause and let you think about it, so I'll just give you the answer. When a car is very close to you, your eye can easily tell that it has two bright headlights. However, when that car is one mile away from you, are you certain that you would still be able to tell? Your eye can tell that two distinct light sources are distinct if the angle that separates them is greater than 1/60th of a degree (a unit of measurement called an arcminute; an arcsecond is 1/60th of an arcminute). If those two light sources are separated by an angle smaller than this (which happens if two lights separated by 6 feet are about 4 miles away from you), you would see them blurred together, appearing as a single light source. Click on the Start button in the Flash animation below to see the animation and note at what point you see two headlights.
This is a type of calculation that will come up repeatedly. So, let's do an example here. If you consider yourself standing, observing the car from a distance, you can picture a right triangle with you at one point (near the vertex with the angle labeled in the image below).
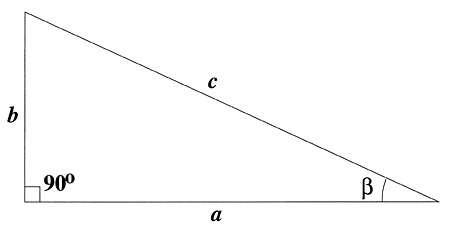
If the separation between the headlights is the side labeled b, then the distance between you and the car is the side labeled a. You can ask how far from you the car must be for the angle to be equal to 1 arcminute. The value of the tangent of is equal to b/a, so, if you do the calculation below, you find:
or
If .
You can do the same experiment on stars. If two stars are separated by more than an arcminute on the sky, you are likely to be able to tell that they are two distinct stars just with your eye. If two stars are so close together that they cannot be split by your eye, with a telescope you may be able to resolve them into two distinct point sources of light. A rule of thumb is that:
The angle that a telescope can resolve is inversely proportional to the size of the aperture of the telescope.
That is, the larger the aperture of the telescope, the smaller the angle it can resolve. Mathematically, you can say that the minimum angle a telescope can resolve, , is proportional to the wavelength of light you are observing divided by the diameter of the telescope, or:
However, this simple rule of thumb only works for telescopes on the Earth with apertures less than about 30 cm. The light from a point source in space coming towards Earth passes through our atmosphere. Turbulent motion in different layers of air in the atmosphere blurs the light from stars into blobs about 1 arcsecond in width (this is why stars appear to twinkle). Thus, even if a telescope is technically capable of resolving two light sources separated by less than 1 arcsecond, the atmosphere will blur them out, causing them to appear as one blob of light rather than two.
The effect of the atmosphere on our view of the sky is called “seeing,” and it varies by location on the sky and over time. If you observe an object near the horizon, you are looking through a path with the maximum amount of atmosphere between you and the object, so the seeing will be bad and the stars will be blobs larger than 1 arcsecond. If you look towards your zenith, you are looking through the least amount of atmosphere, so the stars will appear sharper than those at the horizon. Sometimes the atmosphere is more turbulent, so you can have nights where the seeing is excellent and the stars appear smaller than 1 arcsecond, and at other times the seeing can be poor and stars can appear to be up to 5 arcseconds in diameter or more!
In order to maximize the usefulness of telescopes, astronomers build them on top of the highest mountains in the world (for example, Mauna Kea in Hawaii). At these heights, you are above a good fraction of the atmosphere, and the seeing is better than at sea level. Even better is to put a telescope in orbit, like the Hubble Space Telescope. Hubble is in orbit about 350 miles above the Earth, so its view of the sky does not suffer from “seeing” caused by Earth’s atmosphere. For this reason, the average Hubble image of an astronomical object is ten times sharper than most ground based telescopes can achieve.
Watch this!
Astronomers can actually correct for the effect of seeing. For example, watch this movie of a technique called speckle interferometry. In the movie, that weird blob on the left that looks filled with "speckles" of light is really what our eyes and telescopes see when they look through the atmosphere at two stars. The light from the stars hits the Earth's atmosphere, and the stars' light appears blurred and appears to bounce around, seeming to come from different parts of the sky. But astronomers can use computers to measure the pattern of speckles and recreate what the image would look like without any atmosphere. The image on the upper right is a reconstruction of speckles, showing that what looks like a big blob is the light from two stars, not one.
It turns out that the group that produced this movie took their website down, so the link above takes you to another set of course materials made by folks who captured a local copy of the movie.
Besides speckle interferometry, today telescopes are being outfitted with systems called adaptive optics, which can make the corrections for atmospheric distortion in real time. When those systems are used, they can improve the angular resolution of a telescope on the ground to perform as if it were in space, above the distorting effects of the atmosphere.
Watch this!
At YouTube, they have a movie of an adaptive optics system being used to observe a binary star. About halfway through the movie, the system is switched on.