Additional reading from www.astronomynotes.com
Before returning to open clusters and globular clusters, we are going to revisit the topic of stellar lifetimes, but this time in some more depth. Recall from Lesson 5 on pages 4 and 5 that we talked about how you might quickly estimate the time a star can remain on the Main Sequence and that O stars live substantially shorter lifetimes than M stars. We can actually derive a relationship for the lifetime of a star using what we know already about stars.
From our study of binary stars, we are able to calculate the mass of the stars in the binary system. If you know the distance and the apparent brightness of a star, you can also calculate its luminosity. So, simply using observational data, we have learned that stars along the Main Sequence are a sequence in mass. O stars are the most massive, then B stars, then A, F, G, K, and M stars are the least massive. Since the Main Sequence is also a sequence in luminosity—that is, O stars are the most luminous, then B, then A, F, G, K, and M stars are the least luminous—there must be a relationship between mass and luminosity. If you plot the masses for stars on the x-axis and their luminosities on the y-axis, you can calculate that the relationship between these two quantities is:
This is usually referred to as the mass-luminosity relationship for Main Sequence stars. For a sample plot of this relationship see:
Given our theory for the structure of stars, you can understand where this relationship comes from. Stars on the Main Sequence must be using the energy generated via nuclear fusion in their cores to create hydrostatic equilibrium. The condition of hydrostatic equilibrium is that the pressure is balancing gravity. Since higher mass means a larger gravitational force, higher mass must also mean that higher pressure is required to maintain equilibrium. If you increase the pressure inside a star, the temperature will also increase. So, the cores of massive stars have significantly higher temperatures than the cores of Sun-like stars. At higher temperatures, the nuclear fusion reactions generate energy much faster, so the hotter the core, the more luminous the star.
If you actually look at the equations that govern stellar structure, you can derive from those equations that:
where the exponent varies a bit for stars of different masses, but, in general, is approximately equal to 3.5, as is seen to be the case with the observed masses and luminosities for stars in binary systems.
Below is a plot that obeys this relationship and gives the theoretical calculations of a star's luminosity given its initial mass on the Main Sequence.
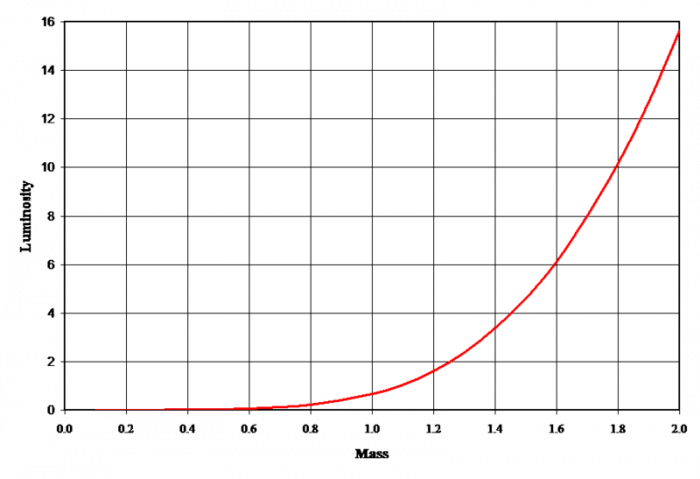
Now, let's revisit the topic of stellar lifetimes. The amount of fuel that a star has available for fusion is directly proportional to its mass. The luminosity measures how quickly the star is using that fuel, so, in general, a rough estimate of the lifetime of a star is:
but, you can substitute in using and determine that:
As we continue our study of star clusters, keep this in mind—the more massive a star, the faster it lives its lifetime, and, given the exponent of this relationship, it isn't a linear relationship. That is, a 10 times more massive star doesn't live a lifetime 10 times shorter than the lower mass star, but approximately a 316 times shorter lifetime than the lower mass star!