Increasing Atmospheric Albedo

There are a couple of ideas for making the atmosphere reflect more sunlight, including brightening clouds and adding aerosols (tiny particles, either solids or liquids, that stay suspended in the atmosphere for a relatively long period of time).

Cloud Albedo Enhancement

The basic idea here is to make clouds brighter by increasing the concentration of tiny droplets of water that make up the clouds. It has long been recognized that in parts of the world that are dustier, the clouds tend to be brighter because of a higher concentration of water droplets. The tiny water droplets in clouds form around even tinier particles called Cloud Condensation Nuclei (CCN) — the more CCNs you have, the more water droplets form, the brighter the clouds are, the more sun they reflect. It has been suggested that spraying tiny salt crystals derived from the oceans would serve this purpose, and this, along with the fact that the oceans cover 75% of the Earth, means that this would be done over the oceans. The troposphere (lower part of the atmosphere where clouds form) is a dynamic place, which makes the effectiveness of this approach somewhat difficult to predict, but in theory, it could provide enough of an albedo increase to accomplish the cooling we might want (a couple of degrees C). It is estimated that something like 1500 ships equipped to extract the salt particles and inject them into the atmosphere would be needed — these ships do not exist at present, and they would have to be custom-made. The cost of this approach is a bit uncertain, but is probably not excessive. The main drawbacks of doing something like this include the uncertainty about how this would affect weather in cities near the oceans and the fact that this would not address the problem of ocean acidification.

Stratospheric Aerosols

We could reduce the amount of solar energy reaching the surface and thus cool the planet by making the atmosphere more reflective through the injection of sulfur aerosols into the stratosphere (above the troposphere). We know that this works because of the cooling that follows large, explosive volcanic eruptions that inject tiny aerosols (particles) of sulfate (SO₄) into the stratosphere. Based on the volcanic eruptions, we can estimate how much sulfur is needed to counteract a doubling of CO₂ — about 5 Tg of S per year (one Tg or teragram is 10¹² g), which is about half the amount that injected into the atmosphere by the eruption of Mt. Pinatubo in the Philippines in 1991.

Sulfate aerosols injected into the stratosphere by planes or balloons would reflect and scatter sunlight before it hit the Earth’s surface — this would reduce the temperature of the Earth. The sulfate has a short residence time in the atmosphere, so it would have to be continuously replenished — but this would still be the cheapest way to stop and even reverse global warming. There are, however, many drawbacks to this kind of geoengineering scheme.

Credit: David Bice © Penn State is licensed under CC BY-NC-SA 4.0

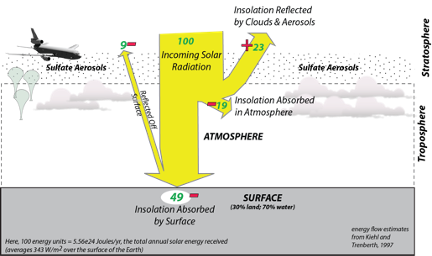
The estimated cost of this would be on the order of \$50 billion per year (consider that the US military expenditures are about \$750 billion per year). These particles have a limited residence time (1-2 years) in the stratosphere, so this would require continual injection via airplanes or balloons. The costs of doing this are surprisingly small (as low as \$50 billion per year), but it would have to be maintained — if we were to start down this path and then suddenly realize that it was a mistake and stop, we would face a truly shocking period of rapid warming. This is because we would probably continue to burn fossil fuels and emit more CO₂ into the atmosphere.

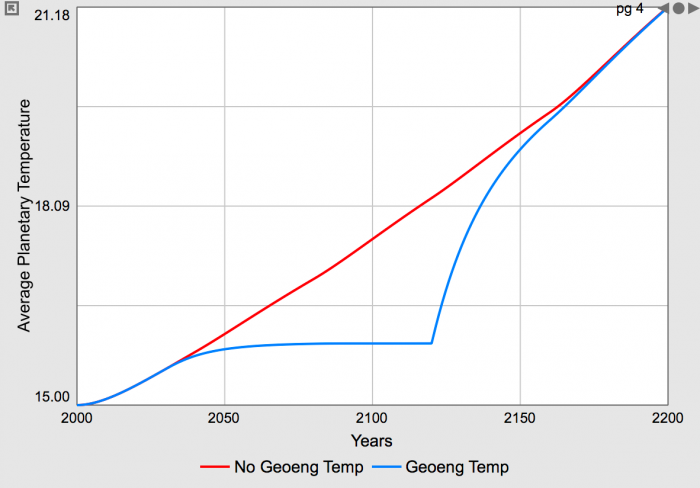
This scenario is illustrated in the figure below, from a simple climate model like the one we used in Module 4, modified to include a sulfate aerosol geoengineering scheme.

Graph on Average Planetary Temperatures.

This figure shows the consequences of halting a sulfate aerosol geoengineering scheme. The red curve shows the average planetary temperature in °C resulting from continued burning of fossil fuels, with a rise of 6°C by the year 2200. The blue curve shows the temperature for a model where sulfate aerosols are injected (beginning in the year 2030) at a rate designed to keep the average temperature at 16°C — this model has the same increase in carbon emissions as the case represented by the red curve. This alteration of the climate is then halted in the year 2120, and the temperature rises rapidly to catch up with the red curve, including an early period where the temperature rises by more than 2°C in about 10 years, which is a rate of warming that is about 20 times greater than what we have experienced over the last 100 years.