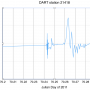
Part 2: Calculating the speed of a tsunami using DART data from 2011
On 2011/3/11 near Honshu Island, Japan (38.322°N, 142.369°E) at 5:46:23 (UTC), a magnitude 9 earthquake occurred. You will inspect the records of 13 DART stations that recorded the tsunami, use them to calculate the speed of the tsunami, plot the stations and the earthquake on a world map, and then answer a set of questions about the data and your observations. For this part of the problem set, I downloaded the freely available data and made the plots for you. Later in this class, you'll have to do the data processing yourself, but not this time. If you want to check the raw data out and see a nice map, this is where to go: 2011 Tohoku Japan DART Data

Use "Part 2" of your problem set worksheet to record your work. View the DART station records for this activity. You can also click on the thumbnails in the table below to see each station's data separately.
In general, you don't have to write a whole page of calculations for each station like I do in my examples, I just wanted to be thorough so you can see my procedure. On the other hand, if you don't show any work it is harder for me to give you partial credit if you make a mistake (see my grading rubric, below).
2.0 Using Google Maps, make a map of the location of both earthquakes, the tide gauge stations from Part 1, and the DART stations from Part 2. When you are done with your map, save it, make a link to it, and paste the link into your worksheet. Or you can take a screenshot of your map and insert that into your worksheet.
Video: How to Make a Map with Google Maps (3:18)
PRESENTER: So when you first get to Google Maps, it'll probably present you with a map of the place where you are, if it knows where you are. Then, if you click this little hamburger over here, and you get a menu. And one of the things you can click on is My Maps. If you've never made a map before, then you'll just get a welcome screen. If you've got something you've already made, then you will be shown a menu with those. But anyway, you can create a new map. And the easiest thing I think to do-- is to just type in the latitude and longitude of the place marker that you want to set. So why don't we put in the location of the Japanese earthquake? There. And it drops the place marker in the ocean. That's fine. So click this little plus here. And then, you want to edit this. So let's call this earthquake. We can also edit what kind of an icon it looks like. Here. And I don't know, gee, this crisis menu is a lot of fun. You can have everything from infestation, geckos, to a ninja with a throwing star, or something like that. Ooh, look, here's one that looks like a tsunami. Maybe that's going to work for us. [INAUDIBLE]. Now you're all set. Let's add another. So here we go with that close by station that we were using for all of our other examples. Drops a placemark there. And why don't we edit that? We'll call it station 21418. Great. We'll add another one just for fun. But I-- my guess is that you've figured it out now. Here is a station that is far away. And that's going to drop another place marker there. We're going to add this one. Station 32412. Save it. OK, now at the end, once you've got everything there, you might want to just zoom out and verify these things are where you think they're supposed to be. Yep, you've got an earthquake off the coast of Japan. A couple of stations. One is close by. One is not close by. At the end, you want to give your map a title. And then, click the Share button. If you forgot to give your map a title, it's going to remind you that it wants you to do that. It's just [INAUDIBLE]. And you can also get a link. And if you want me to be able to see your link without having to log into Google, you can change this so that it's public with anyone who has the link. And you can share it with grandma, too. All right. That's all.
2.1 You already worked with Julian days in Part 1. Now we are going to work with time as expressed in fractions of a day. The earthquake happened on 2011/3/11 at 5:46:23. What is the Julian day of this time, exactly, as expressed in decimal form?
Video: Julian Day (2:22)
PRESENTER: All right, so we're going to convert January 16, 2016, at nine hours, 54 minutes, and 31 seconds into Julian day. So the Julian day is 16 because we're in January. That's pretty easy. In order to convert the time, we need to know how many seconds there are in each of these parts, and then we're going to divide by the total number of seconds in the day. So what we know is that there are 60 seconds in one minute. There are 60 minutes in an hour, and there are 24 hours in a day. And that means if you multiply 60 by 60 by 24, then you can find out that there are 86,400 seconds in one day. I feel like I'm singing that song from rent. Anyway, OK, so here's what we do. We start with nine hours. And we say, all right, nine hours is nine times 3,600, which is the number of seconds in one hour, is going to give us 32,400 seconds. Then we need to convert the minutes. 54 minutes, multiply that by 60 because there are 60 seconds in a minute. And we get 3,240 seconds. And then the 31 seconds, we don't have to convert, because that's already in seconds. All right, and we're going to add up these numbers. And you get this number, 35,671 seconds. We're going to divide that by 86,400 because that's the total number of seconds in a day. All right, so divide by 86,400. And we get 0.4129. Let's do a little reality check because I like to do that when I do math. Is it possible that about nearly 10:00 in the morning, we've gone through about 40% of a 24 hour day? Yeah, that makes sense to me, because noon would be 50%, right? And we're not quite at noon yet, so this looks good. OK, so the answer here finally is that the actual day precisely is 16.4129. That's how you'd express the Julian day with decimals of this date up here.
2.2 Look at each station record and pick the arrival time of the tsunami. I have done the first one for you. Make sure you pick the arrival time of the tsunami and not the arrival time of the seismic waves. Fill in your answers in the table.
Video: Tsunami Arrival Pick (1:56)
PRESENTER: All right, can I just say, before we even start, that this is just such cool data. First of all, this station was really close to the earthquake. And it's sitting at the bottom of the ocean, and you can tell that because the y-axis here is water column height. So this thing is a pressure sensor sitting in five and a half kilometers of water-- which is pretty amazing that we can even build something that will work at five and a half kilometers down, don't you think? Anyway, so in part one, you were looking at tide gauges. And those are really cool, but they're just at the surface, so all they can do is record the height of the water. Whereas this thing, since it's a pressure sensor on the ocean floor, it can record the seismic waves themselves and the tsunami, which is really neat. So here-- the x-axis here is Julian day of 2011, and it's in these fractional parts. So that's helpful since we already know how to do that and work with those numbers. And let's look at the data itself, this wiggly line. All right, so right here is the first big excursion from nothing happening. And that is actually the seismic waves from the earthquake, not the tsunami itself, which is awesome. So the tsunami itself actually comes in right here. And I would mark it down as 70.26 as the arrival time. What's really neat is that when you look at stations that are farther and farther away in the rest of this problem set, you're going to see that the time between the earthquake arrival and the tsunami gets bigger and bigger and bigger. And that's because the seismic waves are just faster. The tsunami is pretty fast, but not as fast as seismic waves. So I don't know. I feel like if I were like a high school physics teacher and I wanted students to do those boring problems, like two trains leave the station and one is traveling at this speed and the other one's traveling at some other speed, and how far apart will they be at time x, y, and z-- well, this is that exact problem. It's just cool because it's real data. It's a real thing that happens in the Earth, you know? So check it out. You'll see it when you look at this data. It's just so neat. It's awesome.
2.3 Calculate the tsunami travel time to each station by subtracting the origin time from the arrival time. (Now aren’t you glad you converted the origin time to decimals!!). I’ve done the first one for you. Your answers will be in fractions of a day, so convert to hours. Fill in your answers in the table.
Video: Tsunami Travel Time (0:58)
PRESENTER: All right. This is how you calculate the travel time to one of your stations. We'll stick with station 21418. That's our example station. So we picked the arrival time at 70.26, so we just need to subtract the origin time of the earthquake, which we've already calculated. And here is the answer we get when we subtract these numbers, 0.0195. And remember, this is in days. But we want to convert this to hours because later, we're going to calculate the velocity of the tsunami. And we want that to be in kilometers per hour. So if we multiply by 24 hours in the day, then we can make this number be hours. And when we do that, we get 0.468. So that is the number of hours it took the tsunami to get from the earthquake to where the station is-- a little less than half an hour.
2.4 Calculate the epicenter-to-station distance along the great circle path between the two locations. We use the great circle path formula because we are calculating distance on the surface of a sphere. Here is the formula for great circle distance: cos(d) = sin(a)sin(b) + cos(a)cos(b)cos|c| in which d is the distance in degrees, a and b are the latitudes of the two points and c is the difference between the longitudes of the two points. Multiply the answer by 111.32 to get from degrees to kilometers. Jean-Paul Rodrigue, at Hofstra University, gives an excellent explanation and tutorial of how to calculate the distance along a great circle path. I’ve done the first one for you. Fill in your answers in the table.
Video: Great Circle Distance (2:42)
PRESENTER: We need to calculate the distance between our earthquake and each station that recorded the tsunami. So the way to do that is to use the great circle path formula. And here is the formula. The cosine of the distance equals the following. OK. So in this formula, A is the latitude of one of our stations we'll call the latitude of the earthquake. B is the latitude of the other point here. A latitude, B latitude. And C is the difference between their longitudes. Take the absolute value of that. So you're going to take the sine of this number, the sine of this number. And then you're going to take the cosine of this number, and the cosine of this number. And you're going to subtract the longitudes from each other. It doesn't matter which, because you're going take the absolute value of that. And take the cosine of that. Multiply all the cosines together. Multiply the sines together. Add those two. And then you have to take the inverse cosine of the answer. And you look at the distance in degrees. Then you multiply by 111.32, and you'll get the distance in kilometers. Now, here are the things that I want to point out that are important. It is important that you know that when you calculate the distance between two points on the surface of a sphere, you need to use the great circle path formula. And I think it's important that you know what that formula is. And I wrote it down right here. But this class is not really meant to be about calculator skills. So if you can automate this in a spreadsheet program or whatever, or you know of a website that will calculate it for you, then that's what you should use, because it will actually minimize the errors of you typing stuff in. I've found a good website that works. And this is it. I've given you the link to this in the course web pages. But you need to be smart about using websites, just like you would if you were looking up information on a website. And that is, you should do a couple of problems yourself, and trust your own math, and then check if the website gives you the same answer or not. And I have checked with this one. So here, I've entered the latitude and longitude of the earthquake, and the latitude and longitude of our station, and it gives me the distance. It is important, when you use a website like this one, that if you have points that are in west longitude, or south latitude, that you enter them in here as negative numbers, or else you won't get the right answer. But I wrote all those down correctly for you in your table of values, so hopefully, that won't trip you up. All right, that's all there is to it.
A nice website that will calculate great circle distance for you.
2.5 Calculate the tsunami speed. To get the speed, you use the formula speed = distance/time. I’ve done the first one for you. Fill in your answers in the table.
Video: Tsunami Speed (2:03)
PRESENTER: All right, we are going to calculate the velocity of a tsunami now. So all we need is to know the formula distance equals rate times time. We just rearranged it, so that rate is over here by itself. Which means we are going to divide distance by time. Well, that's fine, because we already know those, right? We know that the distance is 551.9 kilometers, and we know that the time is 0.468 hours. So this gives us a velocity of 1,179 kilometers per hour. Wow, now I don't know if you have any intuition about how fast a tsunami goes in the open ocean. It's really fast, but it's not quite as fast as this. Wow, so where did we go wrong? Nothing about our method is wrong, but this is a good time to talk about uncertainty. This station is really close to the earthquake, and let's just imagine a thought experiment here where you've got a station that takes a data sample every 15 minutes, OK? But let's say that the tsunami only takes 45 minutes to get to that station. Well, being uncertain plus or minus 15 minutes out of 45 minutes is huge. It's a big uncertainty compared to the measurement you're making, right? Let's say that you've got a station that takes it every 15 minutes, and the tsunami takes eight hours to get there. Well, 15 minutes out of eight hours is not nearly as big of a deal, right? So the absolute value of your uncertainty can matter a lot more, depending on its relationship to the real size of the measurement you're making. And that is a really, really important concept in any branch of science, so just think about that, OK? But anyway, look, this is real data. This is real life. It has uncertainties, and that's OK. It doesn't fit neatly into multiple-choice tests designed by bureaucrats, but that's OK. That's the way it is.
2.6 I want you to think about the uncertainties in the calculations you performed in determining tsunami velocity. One obvious source of uncertainty is measurement precision at each tide gauge station. For example, let’s say that you are working with a DART station that takes a measurement every 15 minutes. This means that picking the arrival time of the tsunami can't be more precise than this. Go back and change the arrival time pick for Station 21418 and for Station 32412 each by 15 minutes. Now recalculate the speed of the tsunami for each of those two stations. How much has your answer changed for each one? Which one is affected more by the uncertainty in arrival time and why?
2.7 What are some other sources of uncertainty in these calculations?
2.8 Calculate the mean speed for the tsunami. Are you surprised by this speed? How does this speed compare to a jet airplane? an Indy car? a bullet fired from a gun? an earthquake P wave? a major league fastball? Pick several items that interest you (they don't have to be any of the examples above if you don't like those) and compare them to the speed of the tsunami.
2.9 Tsunami speed is controlled by water depth. In fact tsunami speed equals the square root of the product of water depth and g, the gravitational constant (9.8 m/s2). Calculate the mean water depth of the Pacific Ocean. To do this, use the mean speed of the tsunami that you calculated in 2.8, convert it from km/hr to m/s, then plug into the equation speed=sqrt(depth*g).
2.10 I want you to think about approaching the question of tsunami speed from a different perspective. What if you wanted to determine how fast a hypothetical tsunami could get from point A to point B? List what would you need to know to make this calculation.
2.11 Now try it! Let's say a large earthquake happens in the Pacific Northwest, approximately at the location of Seattle, generating a tsunami. Determine how long it would take the tsunami to arrive in Hilo, Hawaii.
2.12 What are the sources of uncertainty in the calculation you just did in the previous question?
2.13 There are definitely tide gauge stations on the west coast of Japan and they recorded the tsunami as well. However, we did not use any data from those stations to calculate the speed of the tsunami or to calculate the mean water depth between the earthquake and those stations. Why not? (In order to answer this question you will need to look at the map you made and think about what assumptions we made to do our calculations.)
Submitting your work
Save your worksheet as a Microsoft Word, PDF, or Pages file in the following format:
L2_TsunamiData_AccessAccountID_LastName.doc (or .pdf or .pages).
For example, Cardinals' shortstop Jhonny Peralta's file would be named "L2_TsunamiData_jap27_peralta.doc"
Upload your worksheet to the Tsunami Data problem set assignment in Canvas by the due date on the first page of this lesson.
Grading rubric
I will use my general grading rubric for problem sets when I grade this activity.