Fractionation in Light Ends Unit (LEU)

Fractionation in Light Ends Unit (LEU)

Because of the low molecular weight and high volatility of the constituents in the overhead distillate, the feedstock to LEU can be analyzed on a molecular basis, using, for example, a gas chromatograph. The hydrocarbon range in overhead distillate (over a boiling point of gas to 380°F mid-boiling point) covers carbon numbers C₁ through C₁₀. Because of the relatively simple composition of this feed, the quality of separation in LEU units can be defined in terms of the concentrations of selected hydrocarbon compounds such as propane, butane, and i- butane. Remember that one needs to use the distillation data to define the quality of separation (in terms of ASTM gap, or ASTM overlap) between the adjacent cuts obtained from the side of atmospheric distillation column (Lesson 4).

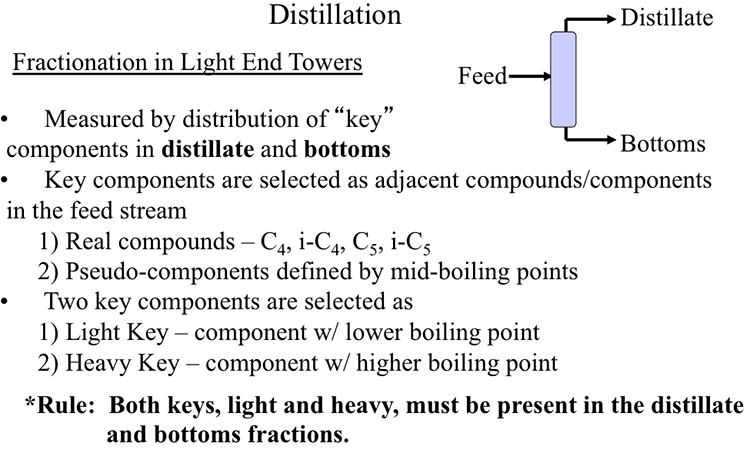
Figure 5.1 shows the separation scheme in light end towers, where the feed is separated into the distillate (low-boiling point) and bottom (high-boiling point) fractions. Considering a depropanizer unit, the distillate will consist mainly of propane and lighter compounds, whereas the bottoms will contain butane and heavier hydrocarbons. To determine the degree of separation in the light end towers, the first step is to select the key components, which may be real compounds (such as butane, or i-butane), or a pseudo component which is defined by the mid-boiling point of the boiling range (i.e., temperature at which 50%_vol of the selected component is evaporated). Two key components (light key and heavy key) must be selected using the two selection rules, as shown in Figure 5.1.

Figure 5.1. Distillation in the light end towers.

Click here for a text alternative to the figure above

Fractionation in Light End Towers

- Measured by the distribution of “key” components in distillate and bottoms.

-Key components are selected as adjacent compounds/components in the feed stream

1) real compounds – C₄, i-C₄, C₅, i-C₅

2) Pseudo-components defined by mid-boiling points

-Two key components are selected as

1) Light Key – component with a lower boiling point

2) Heavy Key – component with a higher boiling point

Credit: Dr. Semih Eser © Penn State is licensed under CC BY-NC-SA 4.0

The key component selection rules are:

1. Light key and heavy key should be adjacent compounds (in terms of boiling points) in the feed stream.
2. Both light key and heavy key must be present in the distillate and bottom fractions.

Once the key components are selected, their concentrations in the distillate and bottom fractions and their respective vapor liquid equilibrium coefficients (K values) can be used in the Fenske Equation to calculate the number of theoretical plates (including a reboiler) needed in the distillation column under the ideal condition of total reflux (100% reflux). Figure 5.2 shows the Fenske Equation and defines all the terms used in the equation. The ideal conditions assumed for using the Fenske Equation include 100% plate efficiency (for perfect separation in a plate) and total reflux in the column where no product is drawn as distillate. Total reflux means the whole overhead product is refluxed back to the column. Obviously, to get data on an actual (not an ideal) case of distillation, one needs to make two corrections to obtain the actual number of plates from the number of theoretical plates used in, or calculated by the Fenske Equation: 1) by assuming an actual plate efficiency to correct for 100% plate efficiency), 2) by assuming a correction factor to correct from total reflux (or infinite reflux ratio to the operational (actual) reflux conditions).

Figure 5.2. Fenske Equation and the definition of all terms in the equation.

Credit: Dr. Semih Eser © Penn State is licensed under CC BY-NC-SA 4.0

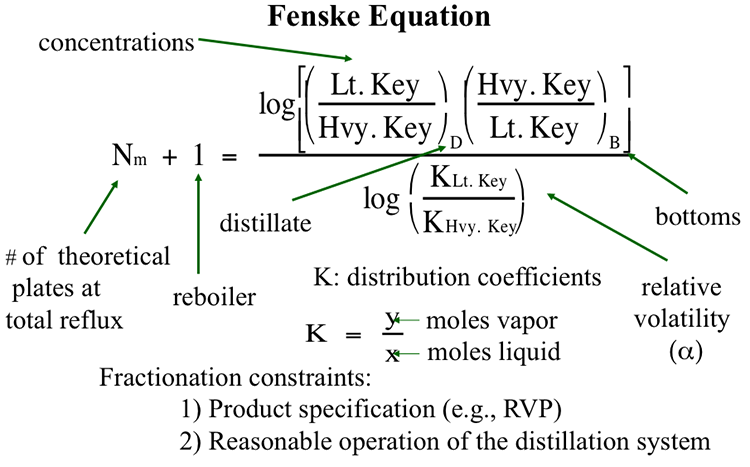
It is common to use an actual plate efficiency of 75% (for plate efficiency correction), and a correction factor of 1.5 (for reflux ratio correction) for the operation under a finite (actual) reflux ratio from the total reflux condition. Therefore, these corrections could be made as follows:

# [actual plates (at 75% efficiency) at total reflux] = [theoretical # plates (at 100% efficiency)]/0.75

# [actual plates (at normal reflux)] = 1.5 x [actual plates (at 75% efficiency) at total reflux]

In other words, making both corrections from #theoretical plates used in Fenske equation to #actual plates after both corrections (for plate efficiency and reflux conditions) would give:

# actual plates = ([#theoretical plates used in Fenske Equation]/0.75) x 1.5