However, as the sophistication of satellite geodesy increased, the need for a truly global, geocentric datum became obvious. The horizontal and vertical information were no longer separate. Since satellites orbit around the center of mass of the earth, a position derived from space-based geodesy can be visualized as a vector originating from that point. So, today, not only are the horizontal and vertical components of a position derived from precisely the same vector, the choice of the coordinate system used to express them is actually a matter of convenience. The position vector can be transformed into the 3-D Cartesian ECEF system, latitude, longitude and height, or virtually any other well-defined coordinate system. However, since the orbital motion and the subsequent position vector derived from satellite geodesy are themselves earth-centered, it follows that the most straightforward representations of that data are earth-centered as well.
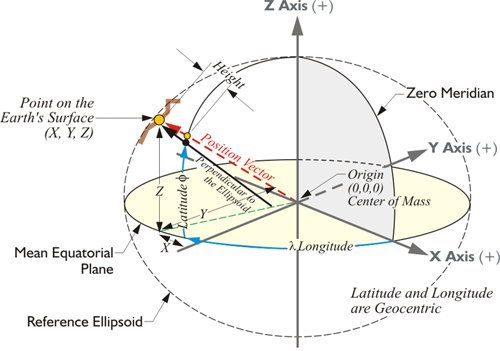
In this representation, there's a point on the Earth's surface. Its XYZ coordinates are indicated from the center of mass of the Earth in a three-dimensional Cartesian system.
However, there are some additions. For example, you see the longitude, symbolized by lambda from the Prime Meridian over to a point on the equatorial plane. From there, you see the latitude up to the position of this point as represented on the ellipsoid, the reference ellipsoid of the datum. Do you remember that an earlier representation of this, the original illustration along this line in the material, had no ellipsoid?
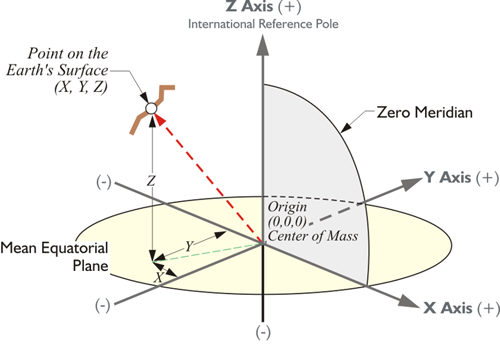
It was simply the XYZ coordinate axes. This is an important distinction. If we're going to have a latitude and longitude derived from an x, y, and z, we have to specify which ellipsoid and which datum (they are not the same thing), is involved. If we are working with the WGS 84 ellipsoid, then we get a latitude and longitude measured along the WGS84 ellipsoid. If we are working with the GRS 80 ellipsoid, we get a different latitude and longitude for exactly the same point on the Earth. If you change the shape of the ellipsoid, the latitude, and longitude changes. Also, the latitude and longitude of a point in the ITRF2014 (2010.0) reference frame is different than the latitude and longitude for the same point in NAD83 2011 (2010.0).
The position vector you see here in red from the center of mass up to the point is different than the black vector that's perpendicular to the ellipsoid. The black vector doesn't go to the center of mass. Also notice that if we're going to go from the position on the ellipsoid up to the actual surface of the Earth, we add a height, an ellipsoidal height. So, we can identify this position on the Earth's surface by an Earth-Centered, Earth-Fixed XYZ coordinate, or we can identify the same point with a geodetic latitude, and longitude, and height. These are just different coordinate systems for expressing the position of the point.
The Development of a Geocentric Model
Satellites have not only provided the impetus for a geocentric datum, they have also supplied the means to achieve it. In fact, the orbital perturbations of man-made near-earth satellites have probably brought more refinements to the understanding of the shape of the earth in a shorter span of time than was ever before possible. For example, the analysis of the precession of Sputnik 2 in the late 1950s showed researchers that the earth’s semiminor axis was actually 85 meters shorter than had been previously thought. In 1958, while studying the tracking data from the orbit of Vanguard I, Ann Bailey of the Goddard Spaceflight Center discovered that the planet is shaped a bit like a pear. There is a slight protuberance at the North Pole, a little depression at the South Pole, and a small bulge just south of the equator. These formations and others have been discovered through the observation of small distortions in satellites’ otherwise elliptical orbits, little bumps in their road, so to speak. The deviations are caused by the action of Earth’s gravity on the satellites as they travel through space. Just as Richer’s clock reacted to the lessening of gravity at the equator, and thereby revealed one of the largest features of the earth’s shape to Newton, small perturbations in the orbits of satellites, also responding to gravity, reveal details of Earth’s shape to today’s scientists. The common aspect of these examples is the direct relationship between direction and magnitude of gravity and the planet’s form. In fact, the surface that best fits the earth’s gravity field has been given a name. It is called the geoid.
