To have a science of place and space, and to investigate whether or not Spatial is Special, you need to set some ground rules for what is possible when it comes to spatial relationships. Spatial Topology is the set of relationships that spatial features (points, lines, or polygons) can have with one another. To make this pretty dry topic a lot more interesting, let’s consider spatial relationships using our personal relationships as a metaphor.
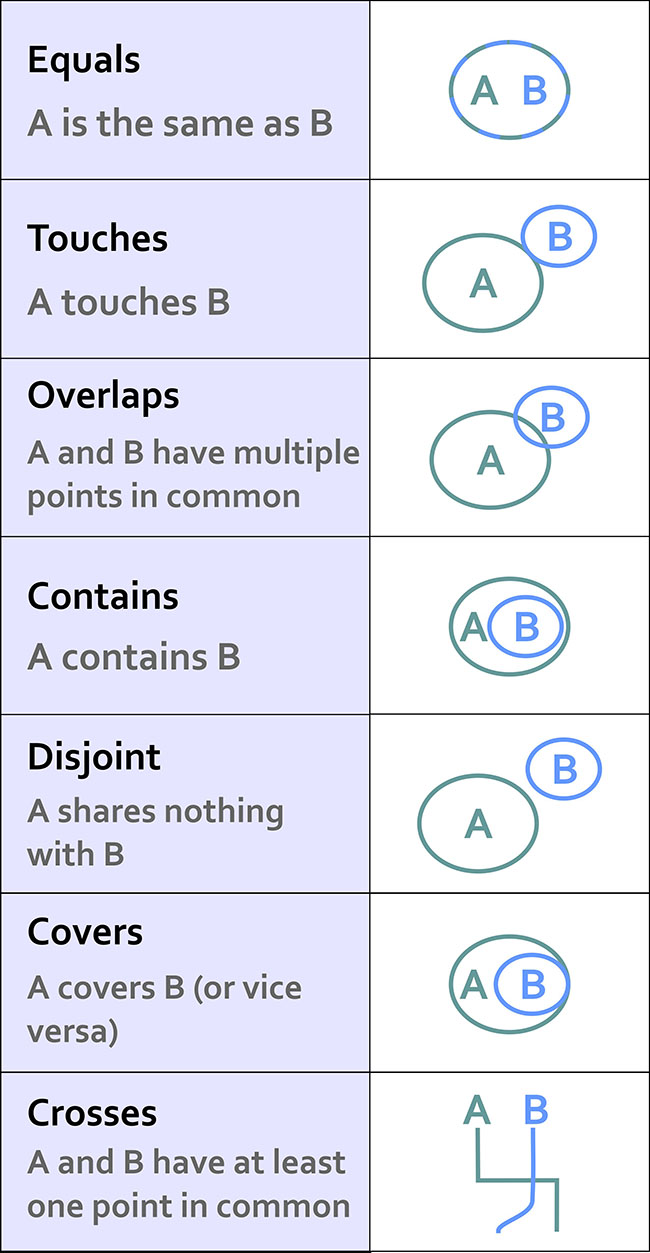
Some common spatial topological relations include:
Equals – A is the same as B
When we first met each other, we felt like we were “one.”
Touches – A touches B
Our first kiss was gentle – no tongue.
Overlaps - A and B have multiple points in common
During our honeymoon we… <deleted>
Contains – A contains B
For 9 months the baby was inside (and much quieter).
Disjoint – A shares nothing with B
Later on, we got sick of each other and watched TV from opposite sides of the room.
Covers – A covers B (or vice versa)
The dog sleeps on top of me, creating a huge amount of heat.
Crosses – A and B have at least one point in common
Although we both know how to find our way home from the grocery store, the only routing point we have in common is our driveway.
This list isn’t exhaustive, but it’s a good starting point. If you really get excited about this stuff (congratulations on being single!) then there is a ton of literature out there to review. I recommend starting with this paper and spiraling out from there.
This stuff may seem a bit dry, but it’s really important because it formalizes the ways in which we can expect things to interact in space. Moreover, knowing all of the possible spatial relations allows us to create great software tools that can take these relationships into account.
Consider what would happen if we didn’t take these relationships into account. Let’s say you have 500 road segments that you’ve digitized to show your neighborhood’s streets. In order to ask a GIS to identify a driving route from one house to another, all of those road segments have to “know” how they are related to one another. So if your street intersects with the next street, we have to specify how both routes are topologically connected. This is how Mapquest or Google understands that when you leave a highway and go on an offramp that there are certain possibilities for navigation (the offramp is a one-way route and connects to a cross-street), and other things you can’t do (the offramp only allows right-hand turns at the end where it intersects with the cross-street). If you didn’t have a theory behind how things can relate, and ways to specify those spatial relations, you’d just have a zillion streets with their basic locations on Earth, but no way to actually use that information for routing.
Almost all of us have experienced the frustrating case where automagical navigation devices and websites have bad or missing topological information. We exit the highway believing we can make a left turn, but it turns out to be a one-way street and we can only go right. Much cursing ensues. Depending on how well we handle this problem, our topological relationship with our significant other may change drastically that night once we finally make it to the hotel.