7.2 Atmospheric Radiation and Earth’s Climate
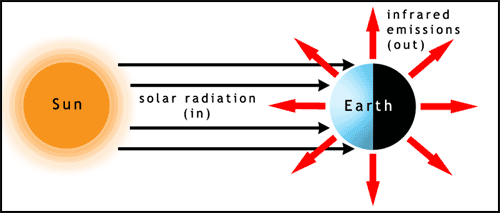
Let’s first look at the general energy balance—the radiative equilibrium—of the Earth system (see figure below). The solar irradiance is essentially composed of parallel radiation beams (or radiances) that strike half the globe. At the same time, outgoing infrared radiation is emitted to space in all directions from both the sunlit and dark sides of the globe. At the top of the atmosphere, the difference of the incoming solar radiation energy minus the amount of solar radiation energy that is scattered back to space (this difference being the amount of solar radiation energy absorbed by the Earth system) must balance the emitted infrared radiation energy for radiative equilibrium to hold. The total amount of solar radiation energy striking Earth per second is equal to the solar irradiance, F (W m–2), times the Earth’s cross sectional area, . Some of the solar radiation energy is reflected by clouds, aerosols, snow, ice, and the land surface back to space and is not absorbed, hence does not contribute energy to raise Earth’s temperature. The fraction that is reflected is called the albedo, and we can account for it by subtracting the albedo from 1 and multiplying times the difference: . The albedo has been estimated to be 0.294 (Stephens et al., 2012, Nature Geoscience 5, p. 691). On the other hand, Earth and its atmosphere radiate in all directions and the radiation can be described by the Stefan–Boltzmann Law, which, recall, is the integral of the Planck function over all wavelengths. Thus the emitted infrared energy per unit area (or emitted infrared irradiance) out the top of the atmosphere is , where we have assumed an emissivity of 1 for the atmosphere at all emitted infrared radiation wavelengths. To get the total energy we must multiply this irradiance by the Earth’s total surface area, . The top of the atmosphere is at an altitude of ~50–100 km above the surface, compared to Earth’s radius of 6400 km, so we will ignore this small difference.
See the video (1:37) below for a more detailed explanation:
To calculate the average temperature at the top of Earth's atmosphere, we need to look at the balance between the solar radiation coming into the Earth's system against the infrared radiation going out of the Earth's system. The solar irradiance is essentially parallel by the time it gets to Earth, so it is intercepted by Earth's cross-section, which is just pi r Earth squared. Since a fraction of the solar radiation is immediately reflected and scattered back out into space-- this is what we call the albedo-- we have to correct the amount of radiation energy that Earth's system absorbed by subtracting off the albedo. On the other hand, Earth radiates in all directions. So assuming Earth's emissivity, than Earth's irradiance is in watts per meter squared. And if we multiply by Earth's surface area, really the surface area at the top of the atmosphere, then we get the energy leaving the Earth's system every second. That is in watts. We can use the laws of exponents to rearrange this equation to get an equation for temperature. When we put in typical values for the earth's system and solar irradiance, we calculate that the radiating temperature at the top of the atmosphere is 255 Kelvin or minus 18 degrees C or 0 Fahrenheit.
Equating the solar radiation energy absorbed by the Earth system to the infrared radiation energy emitted by the Earth system to space gives the equation:
But what is the temperature at the top of the atmosphere, Ttop? Put in the values F = 1361 W m–2, a = 0.294, and σ = 5.67 x 10–8 W m–2 K–4. Therefore,
The temperature at the top of the atmosphere is 255 K, which equals –18 oC or 0 oF. It is substantially less than Earth’s average surface temperature of 288 K, which equals 15 oC or 59 oF. This top-of-the-atmosphere temperature is the same as what the Earth’s surface temperature would be if Earth had no atmosphere but had the same albedo. It is clear from these calculations that the atmosphere, modeled with an emissivity (and hence absorptivity) of 1 over all emitted infrared radiation wavelengths, is creating a difference between the temperature at the top of the atmosphere and the temperature at Earth’s surface.
In particular, let’s look at only the vertical energy balance averaged over the entire globe. We will think of everything in terms of the SI units of irradiance (or energy per second per unit area), which is W m–2. Consider two idealized cases first before examining the actual atmosphere: (1) the no-atmosphere model and (2) the infrared-opaque model.
Let’s build a simple, flat atmosphere with all solar and infrared radiation energy moving only vertically (see figure below). For both models we assume:
- solar irradiance is mostly in the visible (even though in reality half the solar irradiance is in the infrared with wavelengths greater than 0.7 µm);
- Earth's surface emits radiation in the infrared;
- radiation energy flowing up must equal radiation energy flowing down at the surface.
For the opaque-infrared model, we make the following additional assumptions:
- the atmosphere emits radiation in the infrared;
- the atmosphere is transparent to visible radiation;
- the atmosphere is opaque (that is, has an absorptivity of 1) to infrared radiation;
- radiation energy flowing up must equal radiation energy flowing down at every level in the atmosphere.
Please watch the following video (2:18)
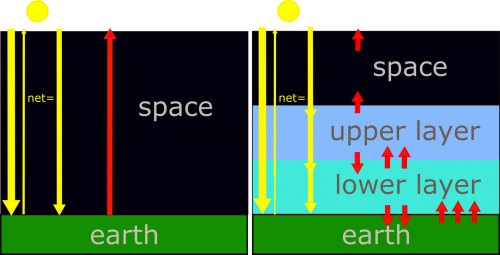
In the simplest climate model there is no atmosphere. Therefore, radiation is absorbed only by Earth's surface. And the atmosphere's emissivity is zero. That solar radiation energy, which is just the difference between the incoming solar radiation energy and the reflected solar radiation energy, equals Earth's infrared radiation energy outgoing to space. Let's represent that amount of energy with a single arrow. At the Earth's surface, and at all levels above, there is one arrow coming down and one arrow going up to maintain radiative equilibrium. Consider next a more realistic climate model, one that has two atmospheric layers that do not absorb the incoming solar radiation, but do strongly absorb infrared radiation. Since they are good absorbers of the infrared, they are also good emitters of the infrared. The radiative equilibrium at each level, the number of arrows, which represent units of radiation energy, must be equal. Starting at the top of the atmosphere, the upper layer must emit one arrow of infrared radiation up to balance the solar visible radiation energy coming down. At the interface between the upper and lower layers there is one arrow of solar radiation energy going down. And the upper layer is emitting one arrow of infrared radiation down because if it is emitting one up, then it must also emit one down, since we are assuming that the layer has a uniform temperature. That puts two down arrows at the interface between the upper layer and the lower layer. To balance these two, the lower layer must be emitting to infrared arrows up. And since the lower layer also has a uniform temperature, it must also be emitting two arrows down to Earth's surface. With one solar and two infrared arrows down to earth's surface, Earth's surface must emit three arrows of infrared radiation up. To emit that much infrared, Earth's surface must be at a higher temperature, since it's irradiance is proportional to its temperature to the fourth power.
In the no-atmosphere model, the only radiating bodies are the Sun and the Earth. (By the way, if Earth had a pure nitrogen atmosphere, the results would be very similar to the no-atmosphere scenario.) The solar radiation passes through the altitude levels where a stratosphere and troposphere would be and the fraction 1 – a of the radiation is absorbed by the Earth’s surface. We assume that Earth’s albedo is still 0.294 so that 0.706, or 70.6%, of the solar radiation is absorbed at the surface with the rest reflected back to space. The Earth’s surface radiates infrared radiation energy back out to space with no absorption at the levels where the stratosphere and troposphere would be. The surface temperature in this model is such that the infrared radiation energy leaving the surface balances the incoming solar radiation energy absorbed by the surface. In terms of the arrows in the figure, there is one down arrow and one up arrow at every level.
| model | no atmosphere |
atmosphere transparent in visible opaque in infrared |
||
|---|---|---|---|---|
| interface | down arrows | up arrows | down arrows | up arrows |
| space–stratosphere | 1 | 1 | ||
| stratosphere–troposphere | 2 | 2 | ||
| troposphere–surface | 3 | 3 | ||
| space–surface | 1 | 1 | ||
So what would the temperature at Earth’s surface be if there was no atmosphere? Equation [7-2] applies to the no-atmosphere case and hence the Earth with no atmosphere has a surface temperature of 255 K. This temperature is the same as the radiating temperature at the top of our Earth with an atmosphere whose absorptivity (and hence emissivity) is 1 at all emitted infrared radiation wavelengths. The surface would be so cold that any water on it would freeze and stay frozen.
Now consider the opaque-infrared model. The atmosphere in this model is identical to the atmosphere modeled in the derivation of Equation [7-2]. Now, however, we will be paying attention to the temperature of Earth’s surface under such an atmosphere. As before, this atmosphere is transparent to all solar radiation energy coming down to Earth’s surface and is opaque to all infrared radiation. “Opaque” means that the infrared radiation is completely absorbed over very short distances (i.e., the absorptivity and emissivity are 1, and the absorption optical depth is great, so by Beer’s Law, very little infrared radiation is transmitted). The atmosphere itself is strongly emitting in all directions, both up and down, and the only infrared radiation that does not get absorbed is that emitted out the top of the stratosphere to space.
We know that the infrared radiation leaving the Earth system must come close to balancing the solar radiation absorbed by the Earth system. Otherwise, the temperatures of Earth’s surface and atmosphere would adjust until this condition was true. So, we will assume radiative equilibrium. Our model is a two-layer model—an upper layer and a lower layer—with a solid Earth beneath them. We are assuming that each layer is at a constant temperature and absorbs all infrared radiation energy impinging on it, and then emits infrared radiation out its top and its bottom in equal amounts (because the layer emits infrared radiation energy in both directions equally). The amount of infrared radiation energy emitted by the layer is determined by its temperature only because its emissivity is set to 1 at all infrared wavelengths. Thus between the upper layer and space, we have one arrow going down and one arrow going up: the outgoing emitted infrared radiation energy exactly balances the incoming solar radiation energy that is absorbed.
The upper layer thus also emits one arrow of infrared radiation down. So, at the interface between the upper and lower layer, the solar radiation and the upper layer's infrared radiation are going down (two arrows). To be in radiative equilibrium there must be enough upwelling infrared radiation from the lower layer to equal the incoming solar radiation energy that is absorbed and the downward infrared radiation emitted by the upper layer (two arrows). But that means that the lower layer must also be emitting the same amount of infrared radiation down to Earth’s surface (two arrows).
At Earth’s surface, there is the incoming solar radiation energy that is absorbed and the tropospheric downward emitted infrared radiation, equivalent to three times the incoming solar radiation energy that is absorbed. Thus Earth’s surface must be radiating upwelling infrared radiation energy equivalent to this incoming energy to maintain radiative equilibrium. So, in this simple model Earth’s surface is radiating three times the energy that the model without the atmosphere does. But to emit this larger amount of radiation the surface must be much warmer than the surface in the model without an atmosphere. We can calculate the surface temperature that would be required using equation [7-2], but adding the downward emitted infrared radiation energy from the troposphere to the solar radiation energy. One way to look at this situation is that the lower layer is providing a source of radiation energy at the Earth’s surface in addition to the solar radiation energy.
Mathematically, we can account for this extra energy near Earth's surface by simply multiplying the solar radiant energy by an IR multiplier, multiplierIR = 3, in equation [7-2]:
This temperature (336 K = 63 oC = 145 oF) is deadly and much higher than Earth’s actual surface temperature, 288 K. So this model also fails to simulate the real Earth. The no-atmosphere model is too cold while the model with a two-layer, infrared-opaque atmosphere is too hot. So we can guess that something in between might be just right.
Indeed this is the case! If you look at the infrared absorption spectrum in Lesson 6, you will recall that there are some wavelengths at which all the infrared is absorbed and others, called windows, at which only a small fraction of the infrared radiation is absorbed. So, we find that a mix of total absorption, partial absorption, and no absorption at various wavelengths gives an atmosphere that allows Earth’s surface to radiate much radiation directly to space at some wavelengths but not at other wavelengths, where troposphere absorption is strong. But a large absorptivity implies a large emissivity so that at those wavelengths for which there is strong absorption there is also emission; however, given that the troposphere is cooler than the surface, the troposphere emits less upwelling infrared radiation energy than it absorbs from the warmer surface underneath. But irrespective of wavelength, emission by the troposphere is downwards as well as upwards, and provides another radiation energy source to heat Earth’s surface. This is called the greenhouse effect, which is poorly named because a greenhouse warms the Earth by suppressing heat loss by convection whereas the troposphere warms the Earth by emitting infrared radiation.
A study by Kiehl and Trenberth (1997, Bulletin of the American Meteorological Society 78, p. 197) determined the contributions to the greenhouse effect. It was shown that 81% of the greenhouse effect is due to greenhouse gases and 19% is due to clouds. Of the greenhouse effect resulting from gases, 60% is contributed by water vapor, 26% by carbon dioxide, and 14% by ozone, nitrous oxide, and methane. Though clouds are an important contributor to the greenhouse effect, they are actually more effective at reflecting solar radiation back to space: clouds cause a greenhouse warming of 30 W m–2 but a reflective cooling of 50 W m–2 for a net radiative cooling of 20 W m–2 (National Research Council, 2008).
In parts of the spectrum where water vapor, carbon dioxide and other gases absorb more weakly, the atmosphere is less opaque. However, if the amounts of these gases are increased, then they will absorb more strongly and thus start emitting more strongly, thus increasing the radiation emitted by the atmosphere to the surface and thus increasing the surface temperature in order for the surface to come into radiative equilibrium. Remember that the energy going out of the top of the atmosphere is still essentially the same as the solar radiation energy coming into the atmosphere that is absorbed. In a sense, by adding carbon dioxide and other greenhouse gases to the atmosphere, we are moving Earth’s surface temperature from being closer to the lower value of the no-atmosphere model to being closer to the higher value of the infrared-opaque model.
In summary, the greenhouse effect has a very dramatic impact on Earth's climate by warming the surface by 33 oC. The greenhouse effect is mostly natural and keeps the Earth habitable. Recall from Lesson 6 that the greenhouse effect probably kept the Earth at a habitable temperature early in Earth's history, when the energy output of the Sun was much lower. Despite water vapor being the most important greenhouse gas, it is condensable and thus has an extremely short lifetime in the atmosphere (about 8 days, easily calculated as the global total precipitable water divided by the global precipitation rate). It is the longer-lifetime greenhouse gases, particularly carbon dioxide, that ultimately have the bigger impact on climate. In fact, climate model simulations show that when carbon dioxide is completely removed from the atmosphere, the Earth's surface temperature drops by more than 30 oC within 30 years, consistent with our simple estimations of the greenhouse effect (Lacis et al., 2010, Science 330, pg. 356). The large temperature drop is possible because the initial cooling due to carbon dioxide reduces the amount of water vapor in the atmosphere, as expected from the Clausius–Clapeyron equation. A positive feedback, called water-vapor feedback, then ensues, leading to further cooling and even lower water vapor, until after 30 years, the water vapor content of the atmosphere is only 10% of its initial value. Water vapor thus follows carbon dioxide, which is why Penn State glaciologist and climate scientist, Richard Alley, refers to carbon dioxide as the "control knob" of the Earth's climate.