8.4 Do you need a weathervane to see which way the wind blows?

Weathervane

Credit: Justin Otto via flickr

Meteorologists use terms such as northeasterlies and southerlies when they describe winds. These terms designate directions that the winds come from. But when we think about the dynamic processes that cause the wind, we use the conventions for direction that are common in mathematics and in coordinate systems like the Cartesian coordinate system. The conversion between the two conventions—math and meteorology—is not simple. However, we will show you a simple way to do the conversion (see the second figure below).

Math Wind Convention

The wind vector is given by U = i u + j v + k w. The wind vector points to the direction the wind is going.

The subscript “H” will be used to denote horizontal vectors, such as the horizontal velocity, U_H = i u + j v (though note that sometimes the symbols V , v_H, and v will be used to denote the horizontal velocity). The magnitude of U_H is U_H = (u² + v²)^1/2. The math wind angle, $α$ , is the angle of the wind relative to the x-axis, so that tan( $α$ ) = v/u and the angle increases counterclockwise as the direction moves from the eastward x-axis ( $α$ = 0^o) to the northward y-axis ( $α$ = 90^o) .

Meteorology Wind Convention

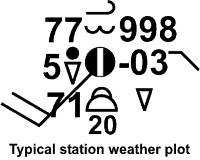
typical weather station plot, lots of numbers and symbols, contact instructor if surrounding content isn't sufficient

In this station weather plot, the wind is blowing from the southwest.

Credit: NOAA National Weather Service

The meteorology wind convention is often used in meteorology, including station weather plots. The wind vector points to the direction the wind is coming from. The angle is denoted by delta, $δ$ , which has the following directions:

Wind Angles
direction wind is coming from	angle $δ$
north (northerlies or southward)	0^o
east (easterlies or westward)	90^o
south (southerlies or northward)	180^o
west (westerlies or eastward)	270^o

Relationship Between Math and Meteorology Wind Conventions

Meteorology angles, designated by $δ$ , increase clockwise from the north (y) axis. Math angles, designated by $α$ , increase counterclockwise from the east (x) axis.

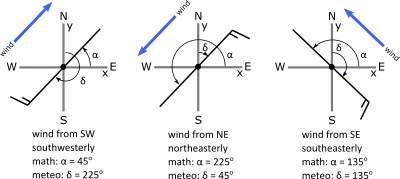
Described below. Line on a compass showing wind blowing & alpha degrees (math) & lower case delta degrees (meteo). Angles are different

Diagram for converting between meteorology and math wind directions for winds blowing from three different directions. Note that the part of the wind line that has the barbs points toward the direction the wind is blowing from. In this diagram, we have extended the line past the center of the axis to indicate the direction that the wind is blowing to because this is the line needed for the math angle.

Credit: W. Brune

In the diagram on the left, the wind is southwesterly, the meteorology angle (measured clockwise from the north or y-axis) δ = 225^o, and the math angle (measured counterclockwise from the east or x-axis) $α = 45^{o}$ . If the wind is northerly (southward), the wind vane points to the north, the wind blows to the south, δ = 0^o and α = 270^o. If the wind is westerly (eastward), δ = 270^o and α = 0^o.

Note that in all cases, we can describe the relationship between the math and the meteorology angles as:

$m a t h a n g l e = 27 0^{o} - m e t e o r o l o g y a n g l e$

When the meteorology angle is greater than 270^o, the math angle will be negative but correct. However, to make the math angle positive, simply add 360^o.

Drawing a figure like those shown in the figure above often helps when you are trying to do the conversion. The following video (2:17) explains the conversion between meteorology and math wind angles using the figure above.

Wind Meteo Math

Click here for transcript of the Wind Meteo Math video.

Meteorology description and wind direction originates from the compass and facing into the wind, where the wind comes from. The mathematical description of wind direction is based on the Cartesian xy grid and tracks the direction that the wind is going. We need to know both. Because the meteorology description, or medial angle, is used in the station weather plot. And we need the mathematical description, or math angle, for dynamics and a numerical weather prediction. Let's look at one example that relates the meteorology and math involves. First note that the grids are related, with positive x corresponding to east and positive y corresponding to north. Now let's add a wind, in this case a wind from the northeast, or northeasterly. From station weather plot the wind is from the northeast. Normally the wind bar would end in the center with a description of cloud cover. But we extend it past the center, toward the direction the wind is blowing, since that would be how we would draw the line and describe the wind direction in the mathematical xy coordinate system. The meteorology angle is measured clockwise from the north axis, just as it is for a compass-- 0, 90, 180, 270, 360, which is the same as 0. The math angle is measured counterclockwise from the x, or east, axis-- 0, 90, 180, 270, 360 or 0. It turns out that the math angle equals 270 degrees minus the meteorology angle. And also therefore the meteorology angle equals 270 degrees minus the math angle. So for this case that we've drawn here the meteorology angle equals 45 degrees. So the math angle equals 270 minus 45, which is 225 degrees. The meteorology angle is drawn clockwise. And the math angle as drawn counterclockwise. If the resulting angle is negative, simply add 360 degrees to make it positive.

Quiz 8-2: Finding coordinates and wind directions.

Find Practice Quiz 8-2 in Canvas. You may complete this practice quiz as many times as you want. It is not graded, but it allows you to check your level of preparedness before taking the graded quiz.
When you feel you are ready, take Quiz 8-2. You will be allowed to take this quiz only once. Good luck!

8.4 Do you need a weathervane to see which way the wind blows?