METEO 300
Fundamentals of Atmospheric Science

10.6 Why do weather maps use pressure surfaces instead of height surfaces?

PrintPrint

10.6 Why do weather maps use pressure surfaces instead of height surfaces?

You can’t find a weather map of winds at 5000 m, but you can find one for 500 mb, which is about the same altitude as 5000 m (see figure below).

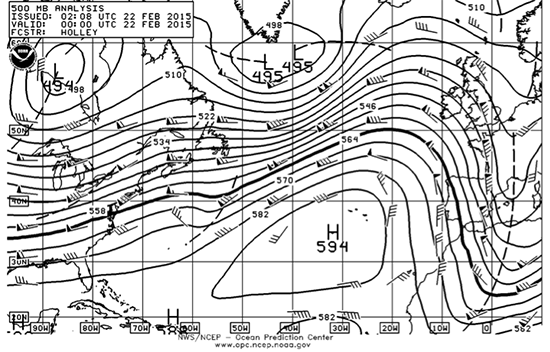
weather map - white with black lines
500 mb winds for 22 February 2015. Numbers are height above sea level in decameters (dam, tens of meters). For example, the height of the 500 mb surface in the high is 5940 m = 594 dam.
Credit: NOAA

We will learn why weather maps use pressure as the vertical coordinate, but for now, we will show that higher altitudes on a constant-pressure surface correspond to higher pressures on an constant-altitude surface.

If we look down on the Earth, then we can plot the isobars as a function of latitude (y) and longitude (x). We can make a second plot of height surfaces on a constant-pressure surface (see figure below). Generally the pressure on average is greater at the equator on a given height surface than it is at the poles. This tilt makes sense if you think about the hydrostatic equilibrium equation because the temperature is greater at the equator than at the poles. Therefore, the scale height is greater, and so pressure decreases with height more gradually at the equator than it does at the poles.

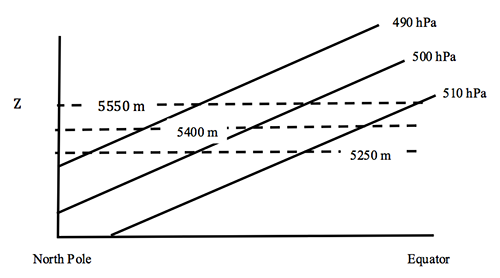
N. pole 2 equator on one axis, Z on other. solid, diagonal lines (490, 500, 510 hPa) intersect horizontal dashed lines (5550, 5400, 5250m)
A schematic of constant-pressure surfaces intersecting with constant-height surfaces from the pole to the equator.
Credit: W. Brune

We can arbitrarily choose one height surface and see how the pressure changes as a function of latitude. We see that it increases from pole to equator (see figure below).

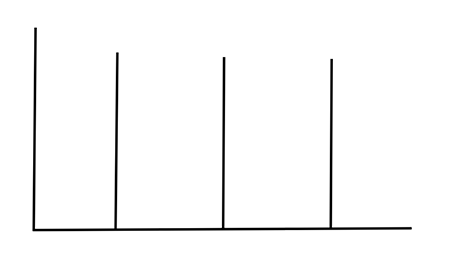
isobars. 3 vertical lines rising from the y axis
A schematic of isobars (constant pressure) on an x–y horizontal map at a constant height surface of 5400 m, as in the figure above.
Credit: W. Brune

If we now arbitrarily choose a constant-pressure surface of, say, 500 mb, then the change in the height on an x–y horizontal plot on the pressure surface also shows an increase from pole to equator (see figure below).

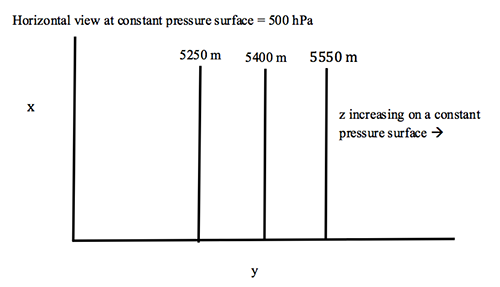
4 vertical lines coming out of y axis, labeled 5250m, 5400m, & 5550m all at pressure = 500hPa
A schematic of lines of constant height on an x–y horizontal map at a constant pressure surface of 500 hPa, as in the figure above.
Credit: W. Brune

Thus, low pressure on constant-height surfaces is related to low heights on constant-pressure surfaces. As a result of the hydrostatic approximation, for every height there is a unique pressure, so we can replace z with p as the vertical coordinate. We can then look at changes in variables as a function of x and y, but instead of doing this on a constant-height surface, we can do it on a constant-pressure surface.

We can now show how the equations of motion change when the vertical coordinate is switched from the height, z, to the pressure, p.

Consider first the pressure gradient force (PGF). The figure below provides a schematic of the math.

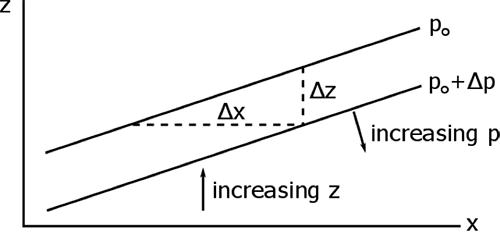
parallel diagonal lines. top labeled P0, bottom P0 +delta p, triangle made by delta x and delta z between lines increasing z, increasing p
A cross section of pressure change on a x–z surface. Note that Δx, Δz, and Δp are all positive and Δp is the same in the horizontal and vertical.
Credit: W. Brune (after R. Najjar)

The slope of the isobar is just the change in z divided by the change in x on an isobar:

Δz Δx → ( ∂z ∂x ) p MathType@MTEF@5@5@+=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaalaaabaGaeuiLdqKaamOEaaqaaiabfs5aejaadIhaaaGaeyOKH46aaeWaaeaadaWcaaqaaiabgkGi2kaadQhaaeaacqGHciITcaWG4baaaaGaayjkaiaawMcaamaaBaaaleaacaWGWbaabeaaaaa@4111@

where the subscript “p” means “constant pressure.” Since Δp is the same in the vertical and the horizontal:

( ∂p ∂x ) z Δx=− ( ∂p ∂z ) x Δz ( ∂p ∂x ) z =− ( ∂p ∂z ) x ( ∂z ∂x ) p MathType@MTEF@5@5@+=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOabaeqabaWaaeWaaeaadaWcaaqaaiabgkGi2kaadchaaeaacqGHciITcaWG4baaaaGaayjkaiaawMcaamaaBaaaleaacaWG6baabeaakiabfs5aejaadIhacqGH9aqpcqGHsisldaqadaqaamaalaaabaGaeyOaIyRaamiCaaqaaiabgkGi2kaadQhaaaaacaGLOaGaayzkaaWaaSbaaSqaaiaadIhaaeqaaOGaeuiLdqKaamOEaaqaamaabmaabaWaaSaaaeaacqGHciITcaWGWbaabaGaeyOaIyRaamiEaaaaaiaawIcacaGLPaaadaWgaaWcbaGaamOEaaqabaGccqGH9aqpcqGHsisldaqadaqaamaalaaabaGaeyOaIyRaamiCaaqaaiabgkGi2kaadQhaaaaacaGLOaGaayzkaaWaaSbaaSqaaiaadIhaaeqaaOWaaeWaaeaadaWcaaqaaiabgkGi2kaadQhaaeaacqGHciITcaWG4baaaaGaayjkaiaawMcaamaaBaaaleaacaWGWbaabeaaaOqaaaaaaa@613C@

where the subscripts "x" and "z" mean constant eastward distance and constant height, respectively.

Multiplying both sides by 1/ρ and using the hydrostatic equilibrium equation:

− 1 ρ ( ∂p ∂x ) z = 1 ρ ( ∂p ∂z ) x ( ∂z ∂x ) p =−g ( ∂z ∂x ) p or − 1 ρ ( ∂p ∂x ) z =−g ( ∂z ∂x ) p MathType@MTEF@5@5@+=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOabaeqabaGaeyOeI0YaaSaaaeaacaaIXaaabaGaeqyWdihaamaabmaabaWaaSaaaeaacqGHciITcaWGWbaabaGaeyOaIyRaamiEaaaaaiaawIcacaGLPaaadaWgaaWcbaGaamOEaaqabaGccqGH9aqpdaWcaaqaaiaaigdaaeaacqaHbpGCaaWaaeWaaeaadaWcaaqaaiabgkGi2kaadchaaeaacqGHciITcaWG6baaaaGaayjkaiaawMcaamaaBaaaleaacaWG4baabeaakmaabmaabaWaaSaaaeaacqGHciITcaWG6baabaGaeyOaIyRaamiEaaaaaiaawIcacaGLPaaadaWgaaWcbaGaamiCaaqabaGccqGH9aqpcqGHsislcaWGNbWaaeWaaeaadaWcaaqaaiabgkGi2kaadQhaaeaacqGHciITcaWG4baaaaGaayjkaiaawMcaamaaBaaaleaacaWGWbaabeaaaOqaaiaad+gacaWGYbaabaGaeyOeI0YaaSaaaeaacaaIXaaabaGaeqyWdihaamaabmaabaWaaSaaaeaacqGHciITcaWGWbaabaGaeyOaIyRaamiEaaaaaiaawIcacaGLPaaadaWgaaWcbaGaamOEaaqabaGccqGH9aqpcqGHsislcaWGNbWaaeWaaeaadaWcaaqaaiabgkGi2kaadQhaaeaacqGHciITcaWG4baaaaGaayjkaiaawMcaamaaBaaaleaacaWGWbaabeaaaaaa@723A@

[10.27]

Same for the y direction:

− 1 ρ ( ∂p ∂y ) z =−g ( ∂z ∂y ) p MathType@MTEF@5@5@+=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabgkHiTmaalaaabaGaaGymaaqaaiabeg8aYbaadaqadaqaamaalaaabaGaeyOaIyRaamiCaaqaaiabgkGi2kaadMhaaaaacaGLOaGaayzkaaWaaSbaaSqaaiaadQhaaeqaaOGaeyypa0JaeyOeI0Iaam4zamaabmaabaWaaSaaaeaacqGHciITcaWG6baabaGaeyOaIyRaamyEaaaaaiaawIcacaGLPaaadaWgaaWcbaGaamiCaaqabaaaaa@4831@

[10.28]

So, the geostrophic balance (Equation [10.24], [10.25]) in pressure coordinates becomes:

x-momentum equation:      0=−g ∂z ∂x +fv y-momentum equation:      0=−g ∂z ∂y −fu MathType@MTEF@5@5@+=faaahmart1ev3aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=ribbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dc9Gqpi0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaafaWaaeGabaaabaaeeaaaaaaaaigBHn2Aa8qacaWG4bGaaeylaiaab2gacaqGVbGaaeyBaiaabwgacaqGUbGaaeiDaiaabwhacaqGTbGaaeiiaiaabwgacaqGXbGaaeyDaiaabggacaqG0bGaaeyAaiaab+gacaqGUbGaaeOoaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaeiiaiaaicdacqGH9aqpcqGHsislcaWGNbWaaSaaa8aabaWdbiabgkGi2kaadQhaa8aabaWdbiabgkGi2kaadIhaaaGaey4kaSIaamOzaiaadAhaa8aabaWdbiaadMhacaqGTaGaaeyBaiaab+gacaqGTbGaaeyzaiaab6gacaqG0bGaaeyDaiaab2gacaqGGaGaaeyzaiaabghacaqG1bGaaeyyaiaabshacaqGPbGaae4Baiaab6gacaqG6aGaaeiiaiaabccacaqGGaGaaeiiaiaabccacaqGGaGaaGimaiabg2da9iabgkHiTiaadEgadaWcaaWdaeaapeGaeyOaIyRaamOEaaWdaeaapeGaeyOaIyRaamyEaaaacqGHsislcaWGMbGaamyDaaaaaaa@7694@

[10.29]

These equations can be rearranged to give the horizontal velocity on the pressure surface and can be rewritten as one in vector form:

V g → = g f k → × ∇ → p z MathType@MTEF@5@5@+=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaaFiaabaGaamODamaaBaaaleaacaWGNbaabeaaaOGaay51GaGaeyypa0ZaaSaaaeaacaWGNbaabaGaamOzaaaadaWhcaqaaiaadUgaaiaawEniaiabgEna0oaaFiaabaGaey4bIenacaGLxdcadaWgaaWcbaGaamiCaaqabaGccaWG6baaaa@43A7@

[10.30]

where V g → MathType@MTEF@5@5@+=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaaFiaabaGaamODamaaBaaaleaacaWGNbaabeaaaOGaay51Gaaaaa@369B@ is designated geostrophic velocity and ∇ → p z= i → ∂z ∂x + j → ∂z ∂y MathType@MTEF@5@5@+=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaabaaaaaaaaapeGafy4bIe9dayaalaWaaSbaaSqaa8qacaWGWbaapaqabaGcpeGaamOEaiabg2da9iqadMgapaGbaSaapeWaaSaaa8aabaWdbiabgkGi2kaadQhaa8aabaWdbiabgkGi2kaadIhaaaGaey4kaSIabmOAa8aagaWca8qadaWcaaWdaeaapeGaeyOaIyRaamOEaaWdaeaapeGaeyOaIyRaamyEaaaaaaa@453E@ is on a constant pressure surface.

Geopotential

We can write these equations a little differently by using the concept of geopotential. Geopotential, Φ, is the potential energy per unit mass of an air parcel at a height z, where zero potential energy is defined at the surface (z = 0).

Φ= ∫ o z gdz MathType@MTEF@5@5@+=faaagCart1ev2aqaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlNi=xH8yiVC0xbbL8FesqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9Fve9Ff0dc9Gqpi0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaqaaaaaaaaaWdbiabfA6agjabg2da9maawahabeWcpaqaa8qacaWGVbaapaqaaiaadQhaa0qaa8qacqGHRiI8aaGccaWGNbGaamizaiaadQhaaaa@3CE0@

[10.31]

dΦ=gdz MathType@MTEF@5@5@+=faaagCart1ev2aqaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlNi=xH8yiVC0xbbL8FesqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9Fve9Ff0dc9Gqpi0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaqaaaaaaaaaWdbiaabsgacqqHMoGrcqGH9aqpcaWGNbGaamizaiaadQhaaaa@391B@

[10.32]

In vector form, the velocities become:

V → g = 1 f k → × ∇ → p Φ MathType@MTEF@5@5@+=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaaFiaabaGaamODaaGaay51GaWaaSbaaSqaaiaadEgaaeqaaOGaeyypa0ZaaSaaaeaacaaIXaaabaGaamOzaaaadaWhcaqaaiaadUgaaiaawEniaiabgEna0oaaFiaabaGaey4bIenacaGLxdcadaWgaaWcbaGaamiCaaqabaGccqqHMoGraaa@43F1@

[10.33]
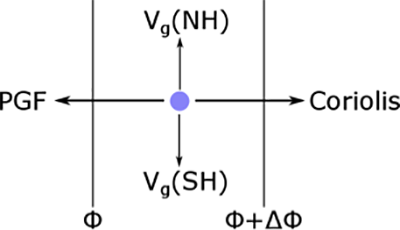
dot with 4 labeled arrows. PGF going left, coriolis going right, Vg(NH) goes up, Vg(SH) goes down. phi and phi+delta phi on either side
Balance between Coriolis and pressure gradient forces and the resulting velocities of the wind in the Northern Hemisphere (NH) and Southern Hemisphere (SH).
Credit: W. Brune

A major advantage of using pressure coordinates is that the gradient of z or Φ is proportional to V g → MathType@MTEF@5@5@+=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCG4uz3bqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaaFiaabaGaamODamaaBaaaleaacaWGNbaabeaaaOGaay51Gaaaaa@369B@ for all pressure levels. This statement is not true for pressure gradients on height levels because you must know the density, ρ, as in Equations [10.24] and [10.25], which varies dramatically with height.

The following video (1:19) provides a good overview of pressure surfaces:

Pressure Surfaces
Click here for a transcript of the Pressure Surfaces video.

This schematic shows the relationship between height surfaces and pressure surfaces. Typically, pressure surfaces slope downward in height from the equator, where it is warmer, to the pole, where it is colder. You were able to show this in Activity 2.2, and you saw it again in Lesson 2.4 on thickness. Note that on the constant height surface, from the equator to the pole, the pressure surface is decreased with latitude. Now it also, on a constant pressure surface from the equator to the pole, the height surface is decreased on the constant pressure surface. Thus, changes in pressure are proportional to changes in height. After a little math, we can show that 1/rho-- that is, one over the density-- times the change in pressure with respect to x or y on a height surface is equal to g times the change in z with respect to x or y on a constant pressure surface. Finally, we note that gdz is just a differential of the geopotential phi, which has units of meters squared per second squared, which are the same units as energy divided by mass. So changes in height on a constant pressure surface are the same as changes in geopotential on a constant pressure surface.