10.9 See how the gradient wind has a role in weather.
Note that the wind speed for gradient flow differs from the wind speed of geostrophic flow. Let’s see why. Start with the geostrophic balance (Equation [10.36]) and rearrange the equation to get an expression for the geostrophic wind speed:
Replacing the pressure gradient force ( ) with –fVg in the gradient balance equation results in an equation that relates these gradient velocities to the geostrophic velocity:
In a regular low (middle, figure below), R > 0 so that Vg > V. The velocity in a curve around a low-pressure area is subgeostrophic.
In a regular high (right, figure below), R < 0 so that Vg < V. The velocity in a curve around a high-pressure area is supergeostrophic.
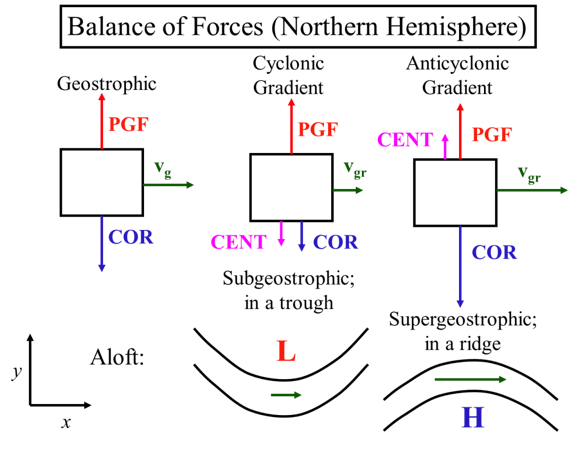
Balance of Forces (Northern Hemisphere)
*Represented as boxes with arrows*
Geostrophic:
PGF arrow pointing up, COR arrow pointing down (about the same size as PGF), vg arrow pointing right
Subgeostrophic in a trough: Low pressure in a trough with a green arrow underneath pointing right
Supergeostrophic; in a ridge: high pressure below a hill with a green arrow above pointing right
Cyclonic Gradient:
PGF up, COR down (smaller than PGF), CENT down (smaller than COR), vgr right (smaller than geostrophic vg)
Anticyclonic Gradient:
PGF up, CENT up (smaller than PGF), COR down (larger than PGF), vgr ( larger than geostrophic vg)
Think of it this way. The pressure gradient force is independent of velocity and so is always there for a given geopotential gradient. In a regular low, the centrifugal and Coriolis forces, both dependent on velocity, sum together to equal the pressure gradient force, whereas for geostrophic flow, only the Coriolis force does. Thus, the velocity in the gradient balance case must be less than the geostrophic velocity for the same geopotential gradient.
So how do subgeostrophic and supergeostrophic flow affect weather?
Supergeostrophic flow around ridges and subgeostrophic flow around troughs helps to explain the convergence and divergence patterns aloft that are linked to vertical motions.
Look at the figure below, starting on the left. Going from geostrophic flow in the straight section to supergeostrophic flow at the ridge’s peak causes divergence aloft. This divergence causes an upward vertical velocity, which causes a low pressure area and convergence at the surface. As the air rounds the ridge’s peak, it slows down to become geostrophic, and then continues to slow down even more as the flow becomes subgeostrophic around the trough, thus causing convergence aloft. This convergence aloft causes a downward velocity, which causes high pressure and divergence at the surface.
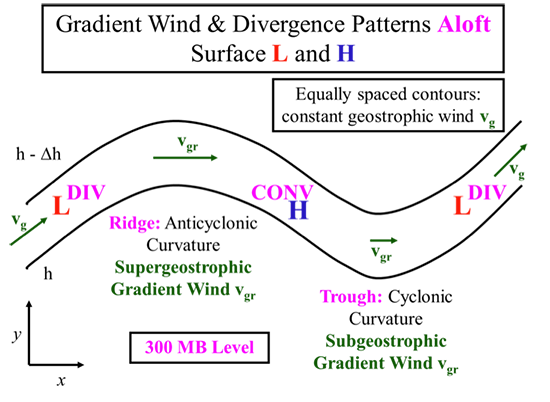
Gradient Wing & Divergence Patterns Aloft, Surface Low and High Pressure
Diagram of a wave shape. It starts as a low-pressure zone with a constant geostrophic wind (vg) moving up along the wave, it is also labeled with divergence, at the ridge of the wave super geostrophic gradient wind vgr is horizontal. The ridge also has anticyclonic curvature. The wave then moves downward, in a high-pressure zone, labeled with convergence until it reaches a trough with cyclonic curvature and subgeostropic gradient wing vgr which is represented by a horizontal arrow. The wave then repeats and vg goes upward toward the ridge from a low-pressure zone that is diverging.
So downwind of a trough is the favored location for divergence aloft, upward motion, and a surface low. Downwind of a ridge is the favored location for convergence aloft, downward motion, and a surface high. Since ridges form around high pressure aloft and troughs form around low pressure aloft, we see that the high aloft is offset relative to the surface low and the low aloft is offset relative to the surface high.
Thus subgeostrophic flow and supergeostrophic flow aloft are directly related to the formation of weather at the surface. Other factors like vorticity are also very important. The video below (1:09) describes how the gradient wind flow aloft can affect surface weather.
Let's see how the gradient wind flow aloft can affect surface weather. Look at how the velocity changes as air flows around the ridge and then a trough aloft. Initially, the velocity is about geostrophic and straight-line flow. As it rounds the ridge, it speeds up. And then it slows down again to geostrophic in the straight section. As it goes through the trough, around the low-pressure loft, it slows down to subgeostrophic and then speeds up to geostrophic in the next straight section. The speeding up causes divergence aloft. And the slowing down causes convergence aloft, just as you learned in lesson nine. You also saw how convergence aloft can lead to divergence at the surface. This contributes to a surface high. And how divergence aloft can lead to convergence at the surface, which contributes to a surface low. Thus, gradient flow contributes to surface weather. We often see a surface low forming on the downwind side of a trough.