10.2 What are the important real forces?
There are three real forces important for atmospheric motion:
- Gravitational Force
- Pressure Gradient Force (PGF)
- Friction
Hence we can sum these real forces:
We put the subscript "a" on these forces to indicate "absolute" because they are true in an inertial reference frame. Thus, in the absolute reference frame,
Let's examine each of these real forces in more detail.
1. Gravitational Force
Recall that the gravitational force on a mass m is simply the weight of the mass, which is given by:
where M is Earth’s mass (5.9722 x 1024 kg), is the distance vector originating from the Earth’s center, and G is the gravitational constant (6.6741 × 10–11 m3 kg–1 s-2). Ignoring the minor effects of topography and the horizontal variation of Earth's density, the real gravitational force points directly towards Earth’s center. The gravitational force per unit mass is simply .
2. Pressure Gradient Force (PGF)
The derivation of the pressure gradient force is similar to what we have already done in Lesson 2.2 to find hydrostatic equilibrium, except that we will look at only the pressure forces in this case, and will serve as a quick review. Consider the x-direction first:
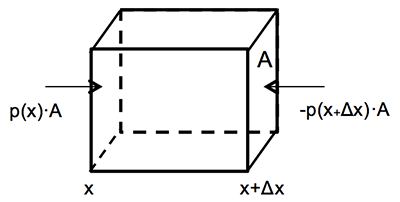
Adding in the y and z directions, we get the 3-D vector form of the pressure gradient force per unit mass:
Example
Let's do a quick calculation of the pressure gradient force from a map of surface pressure on 26 June 2015. Note that Pennsylvania's northern border is about 250 km from its southern border.

Reads: PA is ~250 km high. Isobars are 4 mb apart. Air density ~1.2kg/m3. From 1008 mb isobar to 1016 mb isobar is ~300 km. |PGF| = (1/1.2)* (800 Pa/(300*1000) = 2.2x10-3 m s-2 pointing due west
The following video (1:20) will explain the process:
Let's go through a quick calculation of the pressure gradient force or a low-pressure system that passed over Pennsylvania on June 26, 2015. Note that the pressure increases as x increases. But because the pressure gradient force is minus 1 over the density times the pressure gradient force-- really the pressure gradient acceleration-- is negative. This makes sense since the pressure gradient force would move air from high pressure to low pressure which is to the west in this case. To find the pressure gradient we note that the height of Pennsylvania is about 250 kilometers, which is slightly smaller than the distance between the 1,008 millibar and the 1,016 millibar isobars, which is about 300 kilometers as a distance. So the air density is about 1.2 kilograms per meter cubed. When we put all these numbers together-- that is one over the density times the change in pressure over the change in the distance-- we get that the pressure gradient force, in this case, is 2.2 times 10 to the minus 3 meters per second squared and is directed to 180 degrees, or due west.
3. Friction
We can think of friction as being processes that impede the airflow. There are two different types of friction that meteorologists are concerned with: molecular friction and turbulent friction. Molecular friction is a real force that appears in the conservation of momentum equation whereas turbulent friction is an additional term that arises out of averaging the conservation of momentum equation.
Molecular friction results from the random movement of molecules. Imagine two air parcels moving towards the east. One air parcel is just to the north of the other and is moving a bit faster than the other. Due to random molecular motion, the two parcels exchange air molecules that carry the momentum of their respective air parcels. When molecules collide, some of their momentum is transferred, resulting in the faster parcel (the one to the north) slowing down and the slower parcel (the one to the south) speeding up. There is thus a transfer of momentum from the faster parcel to the slower parcel. This transfer is proportional to the velocity difference between the air parcels and a quantity called the viscosity. The viscosity depends on the fluid in question (air in this case) and the temperature. Fluids with a relatively high resistance to motion, like honey, have relatively high viscosities. Think about air near the Earth's surface. The air right at the surface is stationary due to electromagnetic forces between the air and the surface. Due to molecular friction, the air near the surface will slow down the air just above it, just as that air slows the air a little bit higher. We show without derivation that the molecular friction force (sometimes called the viscous force) per unit mass is to a very good approximation given by:
where ν is the kinematic viscosity, is called the Laplace operator or the Laplacian, and is the air parcel velocity. The viscous force is important for resisting flow and dissipating air flow on small scales, such as for an individual raindrop, but it is not an important force on larger scales when compared to other forces such as gravity and the pressure gradient force (as will be demonstrated in Lesson 10.5).
Turbulent friction is important for larger-scale atmospheric motion, even synoptic-scale motion. The flow in the atmosphere's lowest kilometer or two, called the atmospheric boundary layer is often turbulent, with chaotic large and small swirls of air that, when taken together, have momentum in all directions. During the day, turbulence is generated by convection. During both day and night, turbulence is also generated by wind shear throughout the boundary layer. No matter how turbulence is generated, it provides a drag on the horizontal flow throughout the boundary layer because upward moving air with low horizontal momentum collides with air aloft with high horizontal momentum, slowing it down. This turbulent drag is often referred to as friction, even though the word "friction" really applies only to molecular-scale interactions.
Turbulent friction is not a fundamental force; it is represented in the conservation of momentum equation only after the equation has been averaged over time, space, or both. New terms representing turbulent friction arise from the averaging of the advective derivative, which we will discuss in more detail in Lesson 11. For now, we take the momentum conservation equation and average it so that all of the quantities that we are predicting—like velocity, pressure, and density—really reflect average quantities that vary gradually over space and time. For example, the wind velocity averaged over an hour and over the southeastern quarter of Pennsylvania would be a good example of a quantity one could predict from the averaged momentum conservation equation. On the other hand, a wind gust measured by an anemometer on top of a building would not be a good example of such a quantity.
For a turbulent boundary layer, the turbulent friction per unit mass is a function of four quantities: the dimensionless drag coefficient Cd, the planetary boundary layer height h, the magnitude of the horizontal velocity , and the horizontal velocity itself:
Even though this turbulent drag is not really friction, it is an important resistance to the average horizontal flow on large scales in the boundary layer and so we will keep it, and not molecular friction, as the friction term in the averaged momentum equation. Note that the turbulent drag is greatest within the boundary layer and becomes much smaller above the boundary layer, where it is assumed that the drag coefficient becomes very small.
Inertial (Real) Force Summary
The real forces can be summarized in the following two equations. The first equation represents how the instantaneous velocity of an individual air parcel varies with time. The second equation, which is an average of the first equation, represents how the average velocity of an air mass varies with time. Both equations include acceleration, gravity, and the pressure gradient force. The first equation includes molecular friction and the second equation includes turbulent friction. The first equation is more accurate but the second equation is more practical for applications in weather and climate.