10.3 Effects of Earth’s Rotation: Apparent Forces

Newton’s Second Law applies in an inertial reference frame, which means that the reference frame is not accelerating. A point on the rotating Earth is not following a straight line through space, but instead follows a roughly circular path and hence is constantly accelerating towards the axis of rotation. Therefore, Earth does not provide an inertial reference frame. For an astronaut in distant space observing the weather on Earth, the air motions obey Newton’s Second Law perfectly, but for an Earth-bound observer, Newton’s Second Law fails to capture the observed motion. To account for this crazy behavior, the Earth-bound observer needs to add some apparent forces to the real forces for the math to explain the observed motion from the point of view of someone standing on the rotating Earth.

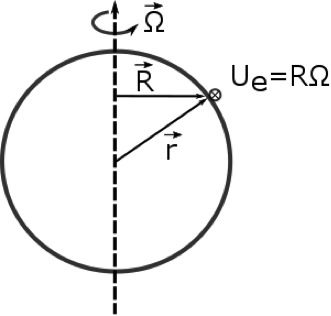
circle labeled to depict earth's rotation

Earth’s rotation is to the east. The symbol ⨂ indicates that the vector

{\vec{U}}_{e}

is going into the page with a magnitude RΩ.

Credit: W. Brune

Suppose we have an air parcel moving through space with a velocity ${\vec{U}}_{a}$ , which we will call the absolute velocity. We want to relate this absolute velocity to $\vec{U}$ , the velocity observed with respect to the Earth reference frame. Let ${\vec{U}}_{e}$ be the velocity of the Earth. Here we only consider the velocity of the Earth due to rotation about its axis (the motion around the Sun is much less important), so ${\vec{U}}_{e}$ is always eastward, greatest at the equator and zero at the poles. The absolute velocity of an air parcel is simply the velocity of the air parcel with respect to the Earth plus the velocity of the Earth itself: ${\vec{U}}_{a} = \vec{U} + {\vec{U}}_{e}$

What is the velocity of the Earth? Consider a specific point on the Earth. Let $\vec{Ω}$ be Earth’s angular velocity vector, $\vec{r}$ be the position vector from the Earth’s center to the point in question, and $\vec{R}$ be the shortest distance vector from the axis of rotation to the point in question (as in the figure above). The magnitude of $\vec{Ω}$ is $| \vec{Ω} | = \frac{2 π}{23.934 hr} \frac{1 hr}{3600 s} = 7.292 \times 10^{- 5} s^{- 1}$ and the direction of $\vec{Ω}$ is determined by the right hand rule (the direction of your thumb when you curl the fingers of your right hand in the direction of rotation and point your thumb towards the North Star). To determine the angular velocity of the Earth, note that we have used the sidereal day length, 23.934 hr, which is the day length when Earth's rotation is measured with respect to the fixed stars (the inertial reference frame).

The following video (:51) will demonstrate the right hand rule:

UE Right Hand Rule

Click here for transcript of the UE Right Hand Rule video.

u sub e is the eastward velocity of the Earth. It is pointed into the page. We know the u sub e equals r-- which is the shortest distance vector between Earth's rotation axis and the point on the surface-- times omega, which is Earth's rotation vector. The units of omega are seconds to the minus 1, which makes it a frequency. Note that u sub e equals r times omega, which is also equal to omega cross r. We can see this if you take your right hand with your fingers pointed in the omega direction and the palm in the r direction. And you fold your fingers into the palm. Your thumb will point into the page, which is the direction of u sub e and is in the positive x direction.

The magnitude of ${\vec{U}}_{e}$ is RΩ, but we need to write ${\vec{U}}_{e}$ as a vector. Note that ${\vec{U}}_{e}$ is pointed into the page in the figure above, which is a direction perpendicular to both $\vec{Ω}$ and $\vec{R}$ . Hence we can use the cross product equation to write an expression for Earth's velocity: ${\vec{U}}_{e} = \vec{Ω} \times \vec{R} = \vec{Ω} \times \vec{r}$ , since the component of $\vec{r}$ perpendicular to $\vec{Ω}$ is $\vec{R}$ . So:

${\vec{U}}_{a} = \vec{U} + \vec{Ω} \times \vec{r}$

[10.10]

We have thus related velocity in the absolute reference frame to velocity in the rotating reference frame.

Now we can consider acceleration. Since $\vec{U} = \frac{D \vec{r}}{D t}$ and ${\vec{U}}_{a} = \frac{D_{a} \vec{r}}{D t}$ we can write:

$\frac{D_{a} \vec{r}}{D t} = \frac{D \vec{r}}{D t} + \vec{Ω} \times \vec{r}$

[10.11]

This equation describes the change in a position of an air parcel with time observed from an inertial reference frame (the derivative on the left) to the change with time observed from Earth’s reference frame (the derivative on the right). Equation [10.11] is general and applies not only to $\vec{r}$ but also to any other vector.

Let’s replace $\vec{r}$ on the left hand side with ${\vec{U}}_{a}$ and $\vec{r}$ on the right hand side with $\vec{U} + \vec{Ω} \times \vec{r}$ since these two expressions equal each other in Equation [10.10]. By making these substitutions, we can relate acceleration in the absolute frame to acceleration in the rotating frame:

\frac{D_{a} {\vec{U}}_{a}}{D t} = \frac{D \vec{U}}{D t} + \frac{D \vec{Ω}}{D t} \times \vec{r} + \vec{Ω} \times \frac{D \vec{r}}{D t} + \vec{Ω} \times \vec{U} + \vec{Ω} \times (\vec{Ω} \times \vec{r})

We can simplify this equation and then we can make sense of it physically. First, $\vec{Ω}$ is not changing significantly with time, so $\frac{D \vec{Ω}}{D t}$ can be set to zero. Second, $(\vec{Ω} \times \vec{r})$ has the magnitude of $Ω R$ and points to the east (by the right hand rule) and thus $\vec{Ω} \times (\vec{Ω} \times \vec{r})$ has the magnitude $Ω^{2} R$ and points toward – $\vec{R}$ . Finally, noting that $\vec{U} = \frac{D \vec{r}}{D t}$ , we end up with the equation:

$\frac{D_{a} {\vec{U}}_{a}}{D t} = \frac{D \vec{U}}{D t} + 2 \vec{Ω} \times \vec{U} - Ω^{2} \vec{R}$

[10.13]

The term on the left is the acceleration in the absolute inertial reference frame. The first term on the right is the acceleration in the Earth reference frame. The remaining terms are the apparent accelerations. The first one is the Coriolis acceleration and the second one is the centripetal acceleration.

We can now combine Equation [10.13] with the version of Equation [10.9] that is averaged to get:

$- \frac{1}{ρ} \vec{\nabla} p + \vec{g} * - \frac{C_{d}}{h} | \vec{V} | \vec{V} = \frac{D \vec{U}}{D t} + 2 \vec{Ω} \times \vec{U} - Ω^{2} \vec{R}$

and then rearrange this equation to get:

$\frac{D \vec{U}}{D t} = - \frac{1}{ρ} \vec{\nabla} p + \vec{g} * - \frac{C_{d}}{h} | \vec{V} | \vec{V} - 2 \vec{Ω} \times \vec{U} + Ω^{2} \vec{R}$

[10.14]

The first three terms on the right hand side of Equation [10.14] are the real forces. The fourth and fifth terms on the right hand side are the apparent forces: the Coriolis force and the centrifugal force, respectively.

Centrifugal Force

The centrifugal force is directed away from the Earth's axis of rotation and is the same type of force that you feel when you are in a car going around a sharp curve. Over its long history, all the material that makes up the Earth has adjusted to the real gravitational force, $\vec{g} *$ , which is directed to Earth’s center, and the apparent centrifugal force that is directed away from Earth’s rotation axis (see figure below).

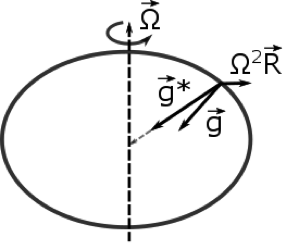
circle illustrating gravity as described in the text

The gravity we feel is the sum of gravity pointed toward Earth’s center and the outward centrifugal force. The effect is greatly exaggerated to show the vectors. The gravity we feel,

\vec{g}

, is perpendicular to Earth's flat surfaces at rest (i.e., oceans).

Credit: W. Brune

The resulting gravity that the Earth and everything on it feels is the vector sum of this real and this apparent force:

$\vec{g} = \vec{g *} + Ω^{2} \vec{R}$

[10.15]

Since the centrifugal force depends on $\vec{R}$ , it is greatest at the equator and zero at the poles. As a result of the centrifugal force, the Earth has become slightly oblate, with an equatorial radius of 6378.1 km that is 0.34% greater than the polar radius of 6356.8 km. Note that $\vec{g}$ is always perpendicular to Earth’s surface, which is very useful because the vertical coordinate is always chosen to be perpendicular to Earth's surface, so that $\vec{g}$ is only in the z direction and, as the figure above indicates, does not point towards the center of the Earth (except at the poles and the equator). The value of g at the equator is 9.780 m s^–2, which is 0.052 m s^–2 smaller than the value of g at the poles, which is 9.832 m s^–2. The centrifugal force at the equator is Ω²R = (7.27 x 10^–5 s^–1)² (6.378 x 10⁶ m) = 0.033 m s^–2, and hence accounts for about 2/3 of the difference in g between the equator and the poles. The rest of the difference is due to the difference in g*, which is overestimated by the difference in equatorial and polar radii--the problem is more complicated than it might appear because Newton's law of gravitation only applies to point masses. At any rate, the difference between g at the poles and equator is small enough for a constant value of g = 9.8 m s^–2 to be suitable for most applications in atmospheric dynamics.

Combining Equations [10.14] and [10.15] yields a more useful form of the averaged momentum conservation in the rotating reference frame:

$\frac{D \vec{U}}{D t} = - \frac{1}{ρ} \vec{\nabla} p + \vec{g} - \frac{C_{d}}{h} | \vec{V} | \vec{V} - 2 \vec{Ω} \times \vec{U}$

[10.16]

We will now move on to a discussion of the Coriolis Force. The following video (3:05) gives a basic introduction.

Coriolis Effect

Click here for transcript of the Coriolis Effect video.

[MUSIC PLAYING]

What's going on here? Every time I throw the ball straight, it seems to bend to the side. No matter what I throw, no matter how straight I throw it, the ball seems to be curving.

Maybe it has something to do with this: That whole time I was spinning, which is why it looks like I'm about to puke.

That curve is created by the Coriolis effect. You may have heard that it makes water in the bathtub spiral down the drain a certain way or that it determines the way a toilet flushes. That's actually wrong. Those are not caused by the Coriolis effect. But the Coriolis effect does create hurricanes and is the reason why Jupiter’s Great Red Spot is spinning the way it is.

So, what is the Coriolis effect? Well, it's what happens when objects moving in a straight line appear to curve because you are rotating. And it affects all kinds of things. It bends the paths of missiles and sniper shots. But how does it work, and how does it create hurricanes?

Right now, it seems like the ball's curving. But let's take a look at what's really happening. My friends and I put together this little experiment using a sort of spinning seesaw. Here, the camera's standing still; it's just hanging from the ceiling. And watch what happens. From the moment the ball leaves my hand, it's just going straight. Let's watch that again, frame by frame. Keep your eye on the ball. You can see that it travels in a perfectly straight line. But what if you're spinning with the seesaw? Look at what happens when you rotate the footage so the seesaw stays sideways and everything moves around it? Now let's follow the path of the ball again but from this new perspective. The trajectory looks completely different. Now let's watch this one frame by frame. From this rotating perspective, it totally looks like the ball is curving. That's crazy because you already saw that exact same throw. Watch it again on the left. The ball is going straight, but on the right, when you're rotating with the seesaw, the ball really looks like it's curving.

You might be thinking, why should I care? I don't spend a lot of time on a spinning seesaw or on a merry-go-round. But you kind of are on a merry-go-round. The earth is constantly spinning. Have you ever seen someone in a movie making fine adjustments on their gun? Well, one effect they're correcting for is the Coriolis effect. The longest sniper shot, which was over 3,000 yards, would have had to correct for a one-foot deviation due to the Coriolis effect.

So, how does the Coriolis effect create hurricanes? Hurricanes form when air rushes from all directions into a low-pressure region. So, imagine there's a low-pressure region between the two of us. Air is going to rush toward the center. Let's see what that looks like from space, from our camera that's hanging from the ceiling. It's not spinning, so the air--or in this case, the balls--are clearly going in a straight line. But if you're rotating with the Earth, or with the seesaw, you'll see the air bend to the right. In the northern hemisphere, this creates hurricanes with counterclockwise spirals. In the southern hemisphere it does the opposite; it creates hurricanes with clockwise spirals. This storm on Jupiter, which is actually bigger than the Earth itself, has been spinning for around 200 years.

So, when you're in a rotating frame, the Coriolis effect seems to exert a very real force on objects. But there is no force; what you observe is just a result of your perspective. And you might be wondering, if this is simply a product of your frame of reference, then could other forces, like gravity or electromagnetism, also just be products of your frame of reference? Of where we live in the universe? Or in the multiverse? For more on that, check out our video "Do We Live in the Multiverse?" There are talking fish. And if you want to find out when new episodes come, click subscribe.

Credit: NOVA PBS

Coriolis Force

The Coriolis force, $- 2 \vec{Ω} \times \vec{U}$ , acts on an air parcel (or any other object) only when it is moving with respect to the Earth. It acts perpendicular to Earth's angular velocity vector and the air parcel's velocity vector. The explanation for the Coriolis force is usually broken into an explanation in the zonal (constant latitude) direction and the meridional (constant longitude) direction.

Zonal Flow (East–West Wind Velocity)

Consider an air parcel that is initially at rest and in hydrostatic balance but is impulsively accelerated to a velocity u to the east (see left side of figure below). Initially when it was at rest, it had the same acceleration as the Earth below it. However, after it accelerated to velocity u, it suddenly had more acceleration than it had before, throwing it out of hydrostatic balance. Look at the change in acceleration that comes from the air parcel suddenly acquiring a velocity to the east, which is just the acceleration after the velocity changes minus the acceleration before the velocity changes and equals (Ω+u/R)²R – Ω²R. To a very good approximation, this change equals the Coriolis force, 2Ωu. There is a vertical component that points up, but there is also a horizontal component of force that points to the right of the motion in the Northern Hemisphere and to the left in the Southern Hemisphere.

Now consider an air parcel that is initially at rest but is impulsively accelerated to a velocity u to the west (see right side of figure below). The air parcel suddenly has less angular momentum than it had before and experiences a decreased centrifugal force. This decrease in angular momentum, to a very good approximation, equals the Coriolis force, 2Ωu, but is pointed toward Earth's axis of rotation. There is a vertical component that points down, but the horizontal component of force that points to the right of the motion in the Northern Hemisphere and to the left in the Southern Hemisphere.

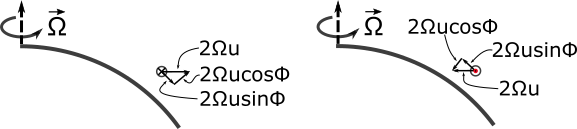
Coriolis force on a particle traveling zonally to the east with speed u as described in the text

Coriolis force on an air parcel traveling zonally (left) to the east, where ⨂ indicates flow into the page, and (right) to the west, where the red dot in the circle indicates flow out of the page, for the Northern Hemisphere. The air parcel speed is u and the latitude is Φ.

Credit: W. Brune

We can write down the accelerations in the y and z directions due to the air moving to the east with speed u:

$Coriolis acceleration in the y direction = \frac{D v}{D t} = - 2 Ω u \sin ϕ$

Coriolis acceleration in the z direction = \frac{D w}{D t} = 2 Ω u \cos ϕ

Meridional Flow (North–South Velocity)

What about an air parcel traveling to the north at a constant altitude? Note that the air parcel moving north starts at a greater distance from Earth’s axis and comes closer to Earth’s axis if it moves at the same height above the surface. Its angular momentum is conserved, so it is moving faster to the east than the Earth beneath it. As a result, it appears to move to the right or the east.

If the same air parcel moves to the south at the same height above Earth’s surface, then it moves to a greater distance from Earth’s rotation axis. Its angular momentum becomes less than that of Earth, it slows down relative to Earth, and it veers to the right of south or to the west.

In both the zonal and meridional flow cases, the air parcel's velocity with respect to the Earth causes the air parcel to have a different angular momentum from the Earth below it. Conservation of angular momentum during that motion requires that the apparent Coriolis force be added in order to describe the observed motion. See the video below (2:11) for further explanation:

Coriolis Explanation

Click here for transcript of the Coriolis Explanation video.

Coriolis force is an apparent force that accounts for motion on a rotating sphere, such as Earth. We can break the explanation of the Coriolis force in two cases-- zonal flow, which is east west, and Meridional flow, which is north south. The explanation for both cases relies on conservation of angular momentum. For zonal flow, imagine an air parcel moving to the east with velocity, u. Angular acceleration is just the angular velocity squared times the radius of rotation. If the parcel is moving at a velocity of u relative to Earth's surface, then it has some extra angular momentum, which is u divided by r. To find the total angular acceleration that the moving air parcel has, we need to square the angular momentum of the air parcel, which is omega plus u divided by r, and then multiply it by r. We then subtract the Earth's acceleration, which is just omega squared r. The difference, to good approximation, is 2 omega times u, which is just the Coriolis force, and, in the case of eastward motion, is pointed away from Earth's axis in the northern hemisphere. Thus, the Coriolis force turns the air parcel to the right for zonal flow. If the air parcel moves to the west, then by the same argument the Coriolis force points towards Earth's rotation axis in the northern hemisphere, which again turns the air parcel to the right. The explanation for the Meridional flow is simpler. An air parcel initially has the angular momentum of the Earth at its latitude. If it moves north at the same height, then it has more angular momentum than the Earth below it. And so it goes faster than the Earth and appears to move to the right. If it moves south at the height, then it has less angular momentum than Earth and appears to slow down relative to Earth and thus appears to move to the right.

Finding the Magnitude and Direction of the Coriolis Force

The magnitude of the horizontal Coriolis force is simply $2 Ω | \vec{V} | \sin φ,$ where φ is the latitude. This magnitude applies to both the Northern and Southern Hemispheres. The direction of the Coriolis force is 90 degrees to the right of the horizontal velocity vector in the Northern Hemisphere and 90 degrees to the left of the horizontal velocity vector in the Southern Hemisphere.

Quiz 10-1: All about forces.

Find Practice Quiz 10-1 in Canvas. You may complete this practice quiz as many times as you want. It is not graded, but it allows you to check your level of preparedness before taking the graded quiz.
When you feel you are ready, take Quiz 10-1. You will be allowed to take this quiz only once. Good luck!

10.3 Effects of Earth’s Rotation: Apparent Forces