2.3 First Law of Thermodynamics

Weather involves heating and cooling, rising air parcels and falling rain, thunderstorms and snow, freezing and thawing. All of this weather occurs according to the three laws of Thermodynamics. The First Law of Thermodynamics tells us how to account for energy in any molecular system, including the atmosphere. As we will see, the concept of temperature is tightly tied to the concept of energy, namely thermal energy, but they are not the same because there are other forms of energy that can be exchanged with thermal energy, such as mechanical energy or electrical energy. Each air parcel contains molecules that have internal energy, which when thinking about the atmosphere, is just the kinetic energy of the molecules (associated with molecular rotations and, in some cases, vibrations) and the potential energy of the molecules (associated with the attractive and repulsive forces between the molecules). Internal energy does not consider their chemical bonds nor the nuclear energy of the nucleus because these do not change during collisions between air molecules. Doing work on an air parcel involves either expanding it by increasing its volume or contracting it. In the atmosphere, as in any system of molecules, energy is not created or destroyed, but instead, it is conserved. We just need to keep track of where the energy comes from and where it goes.

Floating molecules

Credit: Ivana Vasilj via flickr

Let U be an air parcel’s internal energy, Q be the heating rate of that air parcel, and W be the rate that work is done on the air parcel. Then:

$\frac{d U}{d t} = Q + W$

[2.21]

The dimensions of energy are M L² T^–2 so the dimensions of this equation are M L² T^–3.

To give more meaning to this energy budget equation, we need to relate U, Q, and W to variables that we can measure. Once we do that, we can put this equation to work. To do this, we resort to the Ideal Gas Law.

For processes like those that occur in the atmosphere, we can relate working, W, to a change in volume because work is force times distance. Imagine a cylinder with a gas in it. The cross-sectional area of the piston is A. If the piston compresses the gas by moving a distance dx, the amount of work being done by the piston on the gas is the force (pA) multiplied by the distance (dx). W is then pAdx/dt. But the volume change is simply –Adx/dt and so:

$W = - p \frac{d V}{d t}$

[2.22]

Reducing a volume of gas (dV/dt < 0) takes energy, so working on an air parcel is positive when the volume is reduced, or dV/dt < 0. Thus:

$\frac{d U}{d t} = Q - p \frac{d V}{d t}$

[2.23]

Heat Capacity

The heat capacity C is the amount of energy needed to raise the temperature of a substance by a certain amount. Thus, $C = \frac{Q}{\frac{d T}{d t}}$ and has SI units of J/K. C depends on the substance itself, the mass of the substance, and the conditions under which the energy is added. We will consider two special conditions: constant volume and constant pressure.

Heat Capacity at Constant Volume

Consider a box with rigid walls and thus constant volume: $\frac{d V}{d T} = 0$ . No work is being done and only internal energy can change due to heating.

Heating a box with rigid walls.

Credit: W. Brune, after Verlinde

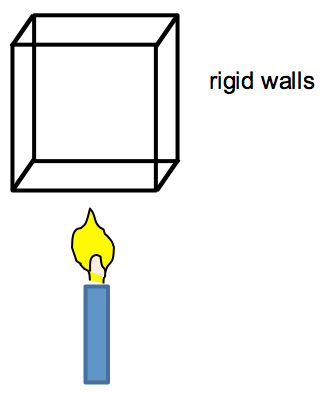
The candle supplies energy to the box, so Q > 0 and dU/dt > 0. The internal energy can increase via increases in molecular kinetic and potential energy. However, for an ideal gas, the attractive and repulsive forces between the molecules (and hence the molecular potential energy) can be ignored. Thus, the molecular kinetic energy and, hence, the temperature, must increase:

$\frac{d T}{d t} > 0$

[2.24]

So,

$Q_{\begin{matrix} c o n s t \\ v o l u m e \end{matrix}} = \frac{d U}{d t} = C_{V} \frac{d T}{d t}$

[2.25]

C_V, the constant relating Q to temperature change, is called the heat capacity at constant volume. Heat capacity has units of J K^-1.

Remember that $C_{v} \frac{d T}{d t}$ is the change in the air parcel’s internal energy.

The heat capacity, C_V, depends on the mass and the type of material. So we can write C_V as:

$C_{V} = m a s s \cdot c_{V}$

[2.26]

where c_V is called the specific heat capacity. The adjective “specific” means the amount of something per unit mass. The greater the heat capacity, the smaller the temperature change for a given amount of heating.

Some specific heat capacity values are included in the table below:

Specific Heat Capacity Values
gas	c_V (@ 0^oC) J kg^–1 K^–1
dry air	718
water vapor	1390
carbon dioxide	820

Solve the following problem on your own. After arriving at your own answer, click on the link to check your work.

Check Your Understanding

Consider a sealed vault with an internal volume of 10 m³ filled with dry air (p = 1013 hPa; T = 273 K). If the vault is being heated at a constant rate from the outside at a rate of 1 kW (1,000 J s^–1), how long will it take for the temperature to climb by 30 ^oC?

Click for answer.

The 1^stLaw can be rewritten as:

$Q = \frac{d U}{d t} + p \frac{d V}{d t} = C_{V} \frac{d T}{d t} + p \frac{d V}{d t} = m a s s \cdot c_{V} \frac{d T}{d t} + p \frac{d V}{d t}$

[2.27]

However, dV/dt = 0 because the vault’s volume isn’t changing. So, we can use the equation, rearrange it and integrate it:

$Q = m a s s \cdot c_{V} \frac{d T}{d t}$

[2.28]

How do we find the mass of the air inside the vault? Use the Ideal Gas Law to find the number of moles and then multiply by the mass per mole!

$m a s s = M_{d r y a i r} \cdot N = M_{d r y a i r} \cdot \frac{p V}{R^{*} T} = 0.029 \cdot \frac{1.013 x 10^{5} \cdot 10}{8.314 \cdot 273} = 12.9 k g$

$Δ t = \frac{m a s s \cdot c_{V} \cdot Δ T}{Q} = \frac{12.9 \cdot 718 \cdot 30}{10^{3}} = 278 s (~ 5 \min)$

Often we do not have a well-defined volume, but instead just an air mass. We can easily measure the air mass’s pressure and temperature, but we cannot easily measure its volume. Often we can figure out the heating rate per volume (or mass) of air. Thus:

$\frac{Q}{m a s s} \equiv q = \frac{m a s s \cdot c_{V} \frac{d T}{d t}}{m a s s} = c_{V} \frac{d T}{d t}; q = c_{V} \frac{d T}{d t}$

[2.29]

where q is the specific heating rate (SI units: J kg^–1 s^–1).

Heat Capacity Constant Pressure

The atmosphere is not a sealed box and when air is heated it can expand. We can no longer ignore the volume change. On the other hand, as the volume changes, any pressure changes are rapidly damped out, causing the pressure in an air parcel to be roughly constant even as the temperature and volume change. This constant-pressure process is called isobaric.

$Q = \frac{d U}{d t} + p \frac{d V}{d t}$

[2.30]

Now the change in the internal energy could be due to changes in temperature or changes in volume. It turns out that internal energy does not change with changes in volume. It only changes due to changes in temperature. But we already know how changes in internal energy are related to changes in temperature from the example of heating the closed box. That is, the internal energy changes are related by the heat capacity constant volume, C_v. Thus:

$Q = C_{V} \frac{d T}{d t} + p \frac{d V}{d t}$

[2.31]

Note that when volume is constant, we get the expression of heating a constant volume.

Suppose we pop the lid off the box and now the air parcel is open to the rest of the atmosphere. What happens when we heat the air parcel? How much does the temperature rise?

It’s hard to say because it is possible that the air parcel’s volume can change in addition to the temperature rise. So we might suspect that, for a fixed heating rate Q, the temperature rise in the open box will be less than the temperature rise in the sealed box where the volume is constant because the volume can change as well as the temperature.

Enthalpy

Enthalpy (H) is an energy quantity that accounts not only for internal energy but also the energy associated with working. It is a useful way to take into consideration both ways that energy can change in a collection of molecules – by internal energy changes and by volume changes that result in work being done.

$e n t h a l p y \equiv H = U + p V$

[2.32]

Enthalpy is the total energy of the air parcel including effects of volume changes. We can do some algebra and use the Chain Rule to write the First Law of Thermodynamics in terms of the enthalpy:

$Q = \frac{d U}{d t} + p \frac{d V}{d t} = \frac{d U}{d t} + \frac{d (p V)}{d t} - V \frac{d p}{d t} = \frac{d (U + p V)}{d t} - V \frac{d p}{d t} = \frac{d H}{d t} - V \frac{d p}{d t}$

[2.33]

If the pressure is constant, which is true for many air parcel processes, then dp/dt = 0 and:

$Q = \frac{d H}{d t}$

[2.34]

Summary

In a constant volume process, heating changes only the internal energy, U.
In a constant pressure process, heating changes enthalpy, H (both internal energy and working).

In analogy with constant volume process, for a constant pressure process, we can write:

$Q_{\begin{matrix} c o n s t a n t \\ p r e s s u r e \end{matrix}} = \frac{d H}{d t} = C_{p} \frac{d T}{d t}$

[2.35]

where C_p is the heat capacity at constant pressure and c_p is the specific heat capacity at constant pressure.

Note that c_p takes into account the energy required to increase the volume as well as to increase the internal energy and thus temperature.

What is the difference between c_p and c_v? You will see the derivation of the relationship, but I will just present the results:

by mole: $c_{(p, m)} = c_{(V, m)} + R^{*}$
by mass for dry air: $c_{p d} = c_{V d} + R_{d}$
by mass for water vapor: $c_{p v} = c_{V v} + R_{v}$

gas	c_V (@ 0^oC) J kg^–1 K^–1	c_p (@ 0^oC) J kg^–1 K^–1
dry air	718	1005
water vapor	1390	1858

Since c_p > c_v, the temperature change at constant pressure will be less than the temperature change at constant volume because some of the energy goes to increasing the volume as well as to increasing the temperature.

Summary of Forms of the First Law of Thermodynamics

$Q = C_{V} \frac{d T}{d t} + p \frac{d V}{d t}$

[2.36]

$Q = C_{p} \frac{d T}{d t} - V \frac{d p}{d t}$

[2.37]

$Q = \frac{d U}{d t} + p \frac{d V}{d t}$

[2.38]

$Q = \frac{d H}{d t} - V \frac{d p}{d t}$

[2.39]

It is often useful to express these equations in terms of specific quantities, such as specific volume (α ≡ V/m = ρ^-1), specific heat at constant pressure (c_p ≡ C_p/m), and specific heat at constant volume (c_V ≡ C_V/m). With these definitions, the first three equations above become:

$q = c_{V} \frac{d T}{d t} + p \frac{d α}{d t}$

[2.40]

$q = c_{p} \frac{d T}{d t} - α \frac{d p}{d t}$

[2.41]

$q = \frac{d u}{d t} + p \frac{d α}{d t}$

[2.42]

$q = \frac{d h}{d t} - α \frac{d p}{d t}$

[2.43]

You can figure out which form to use by following three steps:

Define the system. (i.e., what is the air parcel and what are its characteristics?)
Determine the process(es) (i.e., constant pressure, constant volume, heating, cooling?). Choose the form of the equation by making a term with a conserved quantity go away (i.e., dp/dt = 0 or dV/dt = 0) because then you have a simpler equation to deal with.
Look at which variables you have and then choose the equation that has those variables.

Check Your Understanding

Consider the atmospheric surface layer that is 100 m deep and has an average density of 1.2 kg m^–3. The early morning sun heats the surface, which heats the air with a heating rate of F = 50 W m^–2. How fast does the temperature in the layer increase? Why is this increase important?

What is the system? Air layer. Since we know the heating per unit area, work the problem per unit area.
What is the process? Constant pressure and heating by the sun.
Which variables do we have? $Q = C_{p} \frac{d T}{d t}$

Click for answer.

$Q = F A = 50 W m^{- 2} A$

$C_{p} = c_{p} ρ V = c_{p} ρ Δ z A$

$Q = F A = c_{p} ρ Δ z A \frac{d T}{d t}$

$\frac{d T}{d t} = \frac{F A}{c_{p} ρ Δ z A} = \frac{F}{c_{p} ρ Δ z} = \frac{50}{1005 1.2 100} = 4.2 x 10^{- 4} K s^{- 1} = 1.5 K h r^{- 1}$

This temperature increase is important because it is one of the most important factors in determining whether convection will occur later in the day. We will talk more about instability soon.

Here is a video (1:30) explanation of the above problem:

Dry Air Heating

Click here for transcript of the Dry Air Heating Video.

Let's go through this problem considering the heating of air in the lowest part of the atmosphere, which is called the atmospheric boundary. The sun heats the earth, and then the earth heats the air in contact with it. To see how fast the air will heat up, we need to know the heating rate, but we also need to know the air parcel's capacity. Heating rate is given in watts per meter squared, then we can multiply by some arbitrary area to get the total heating rate. Almost always, atmospheric heating and cooling occurs at constant pressure. Heat capacity, then, depends on the specific heat capacity at constant pressure. But it also depends on the air parcel's mass, which is density times volume. So we need to find the density, if it isn't given to us. You can use the ideal gas law for that. The volume is just the height times the area. So we put the heating rate on the left hand side and the effect of the heating on the parcel on the right. We are assuming a fairly uniform air parcel, so we see we really didn't need to multiply by area at all, since it just cancels out. We can rearrange this equation to get the temperature change for time on the left and all the known variables on the right. And then we can put the numbers in, and we can find out what the change in temperature with time is.

Check Your Understanding

Consider the atmospheric surface layer that is 100 m deep and has an average density of 1.2 kg m^–3. It is night and dark and the land in contact with the air is cooling at 50 W m^–2. If the temperature at the start of the night was 25 ^oC, what is the temperature 8 hours later?

What is the system? Air layer. Since we know the cooling per unit area, work the problem per unit area.
What is the process? Constant pressure and cooling by the land radiating energy to space and the air cooling by being in contact with the land.
Which variables do we have? $Q = C_{p} \frac{d T}{d t}$

Click for answer.

$Q = F A = -50 W m^{- 2} A$

$C_{p} = c_{p} ρ V = c_{p} ρ Δ z A$

$Q = F A = c_{p} ρ Δ z A \frac{d T}{d t}$

$\frac{d T}{d t} = \frac{F A}{c_{p} ρ Δ z A} = \frac{F}{c_{p} ρ Δ z} = \frac{-50}{1005 1.2 100} =- 4.2 x 10^{- 4} K s^{- 1} = -1.5 K h r^{- 1}$

Since the cooling continues for 8 hours, the total amount of cooling is –1.5 K/hr x 8 hr = 12 K or 12 ^oC. Thus, the temperature 8 hours later will be 13 ^oC.

This cooling near the surface creates a layer of cold air near the surface with a layer of warmer air above it. The layering of warm air over colder air creates an temperature inversion, which suppresses convection and lock pollutants into the air layer near Earth's surface.

2.3 First Law of Thermodynamics