5.4.2.1: Derivation of the Diffusivity Equation in Radial-Cylindrical Coordinates for Compressible Gas Flow

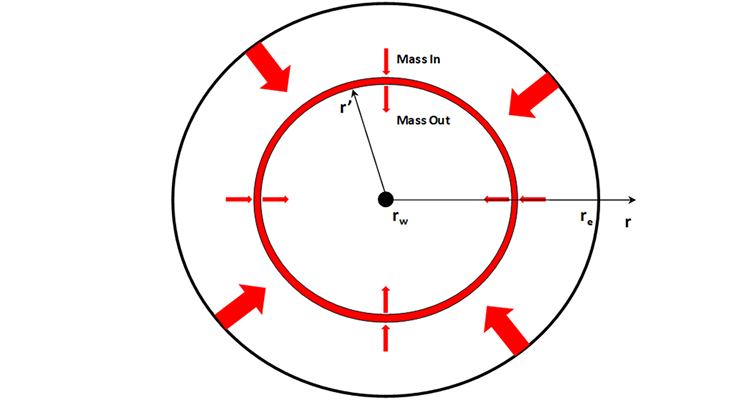
As with the flow of oil, we begin the derivation of diffusivity equation for compressible gas flow with a mass balance on a thin ring or Representative Elemental Volume, REV, in the reservoir as shown in Figure 5.05. This mass balance results in:

$M a s s I n - M a s s O u t = M a s s A c c u m u l a t i o n$

Equation 5.26

We can elaborate on the definitions of terms in Equation 5.26 as:

$M a s s I n = ρ {q]}_{r^{'} + d r} d t = (ρ_{g} q {_{g}]}_{r^{'}} + \frac{\partial (ρ_{g} q_{g})}{\partial r} d r) d t$

Equation 5.27

$M a s s O u t = (ρ_{g} {q_{g}]}_{r^{'}}) d t$

Equation 5.28

and,

$M a s s A c c u m u l a t i o n = ϕ V_{b REV} \partial ρ_{g} = 2 π r d r ϕ h \partial ρ_{g}$

Equation 5.29

Where:

$ρ_{g}$ is the gas density, lb/ft³
$q_{g}$ is the gas rate, ft³/day
$r$ is the radial coordinate in a radial-cylindrical coordinate system, ft
$r'$ is the radius of the representative elemental volume, REV, ft
$t$ is time, days
$ϕ$ is the porosity of the reservoir, fraction
$V_{b REV}$ is the bulk volume of the representative elemental volume, REV, ft³
$h$ is the reservoir thickness, ft

Diagram showing REV in a radial-cylindrical coordinates with arrows showing mass in and mass out pointing toward the center of the circle

Figure 5.05: Representative Elemental Volume, REV, in Radial-Cylindrical Coordinates

Source: Greg King

Substituting Equation 5.27 through Equation 5.29 into Equation 5.26 results in:

$[(ρ_{g} {q_{g}]}_{r^{'}} + \frac{\partial (ρ_{g} q_{g})}{\partial r} d r) - ρ_{g} {q_{g}]}_{r^{'}}] d t = 2 π r d r ϕ h \partial ρ_{g}$

Equation 5.30a

or,

$\frac{\partial (ρ_{g} q_{g})}{\partial r} d r d t = 2 π r d r ϕ h \partial ρ_{g}$

Equation 5.30b

Dividing by the term $r$ $d r$ $d t$ results in:

$\frac{1}{r} \frac{\partial (ρ_{g} q_{g})}{\partial r} = 2 π ϕ h \frac{\partial ρ_{g}}{d t}$

Equation 5.31

Now, substituting Darcy’s Law, Equation 5.06 with $l = - r$ and without the formation volume factor, $B_{g}$ , (we want the flow rate in reservoir ft³/day not SCF/day). The unit conversion factor of 5.615 ft³/bbl converts Darcy’s Law from bbl/day to ft³/day:

$\frac{1}{r} \frac{\partial}{\partial r} [\frac{(5.615) (0.001127) ρ_{g} k_{g} (2 π r h)}{μ_{g}} \frac{\partial p}{\partial r}] = 2 π ϕ h \frac{\partial ρ_{g}}{d t}$

Equation 5.32

If we assume that the permeability, $k_{g}$ , and the thickness, $h$ , are uniform, then we have:

$\frac{1}{r} \frac{\partial}{\partial r} (r \frac{ρ_{g}}{μ_{g}} \frac{\partial p}{\partial r}) = \frac{ϕ}{(5.615) (0.001127) k_{g}} \frac{\partial ρ_{g}}{d t}$

Equation 5.33a

or,

$\frac{1}{r} \frac{\partial}{\partial r} (r \frac{ρ_{g}}{μ_{g}} \frac{\partial p}{\partial r}) = \frac{ϕ}{0.006328 k_{g}} \frac{\partial ρ_{g}}{d t}$

Equation 5.33b

To this point, the derivation for the compressible gas equation is identical to the derivation for a slightly compressible liquid equation. This derivation will begin to deviate now. Applying the definition of density for a real gas (Equation 3.71):

$ρ_{g} = \frac{p M W_{g}}{Z R T_{r}}$

Equation 5.34

Equation 5.34 is a direct result of the Real Gas Law. Substituting into Equation 5.33b results in:

$\frac{1}{r} \frac{\partial}{\partial r} (r \frac{p M W_{g}}{μ_{g} Z R T_{r}} \frac{\partial p}{\partial r}) = \frac{ϕ}{0.006328 k_{g}} \frac{\partial}{d t} (\frac{p M W_{g}}{Z R T_{r}})$

Equation 5.35a

or,

$\frac{1}{r} \frac{\partial}{\partial r} (r \frac{p}{μ_{g} Z} \frac{\partial p}{\partial r}) = \frac{ϕ}{0.006328 k_{g}} \frac{\partial}{d t} (\frac{p}{Z})$

Equation 5.35b

or,

$\frac{1}{r} \frac{\partial}{\partial r} (r \frac{p}{μ_{g} Z} \frac{\partial p}{\partial r}) = \frac{ϕ}{0.006328 k_{g}} \frac{\partial}{d p} (\frac{p}{Z}) \frac{\partial p}{d t}$

Equation 5.35c

Now, we saw in Lesson 3 that for a real gas, the definition of compressibility is (Equation 3.70b):

$c_{g} = - \frac{p}{Z} \frac{d}{d p} {(\frac{Z}{p})]}_{T = T r} = - \frac{p}{Z} \frac{d}{d p} {[{(\frac{p}{Z})}^{- 1}]]}_{T = T r} = \frac{1}{p} - \frac{1}{Z} \frac{d Z}{d p}$

Equation 5.36a

or,

$\frac{d}{d p} {(\frac{p}{Z})]}_{T = T r} = c_{g} \frac{p}{Z}$

Equation 5.36b

Substituting into Equation 5.35c results in:

$\frac{1}{r} \frac{\partial}{\partial r} (r \frac{p}{μ_{g} Z} \frac{\partial p}{\partial r}) = \frac{ϕ c_{g}}{0.006328 k_{g}} \frac{p}{Z} \frac{\partial p}{d t}$

Equation 5.37

Equation 5.37 is the nonlinear diffusivity equation describing the transient behavior of compressible (real) gases. We say that it is Nonlinear because of the functions of pressure appearing in the equation. In this nonlinear form, we cannot solve the equation analytically (exactly). In order to obtain analytical solutions to this equation, we must first Linearize it. We do this in the same manner as we linearized the stabilized flow equations: by use of the Pressure, the Pressure-Squared, and the Pseudo-Pressure Formulations.

Navigation

EMS

Programs

Related Links