In the previous page, we learned how the uniform price auction works: Generators submit supply offers; the RTO aggregates those supply offers to form a system supply curve or "dispatch curve;" and the market clears at the point where the dispatch curve intersects the (fixed) level of demand. Those generators with supply offers below the market clearing point are dispatched, while those with supply offers above the market clearing point are not dispatched.
In the absence of any transmission congestion, every generator clearing the market would get paid the SMP. This is why low cost generators, which we call "inframarginal suppliers," can be very profitable, and the marginal generator earns no profit under the uniform price auction.
When there is transmission congestion, however, things get more complicated because the transmission congestion segments the market. Some areas of the market are on one side of the constraint and some areas are on the other side of the constraint, and no further deliveries can take place between the two areas. If demand increases on one side of the constraint, a generator on that side of the constraint has to be dispatched to meet that demand. If demand increases on the other side of the constraint, a different generator on that side of the constraint has to be dispatched. These generators may have different costs and supply offers, and thus the marginal cost of meeting demand in one location is different from the marginal cost of meeting demand in another location. These location-specific costs are called Locational Marginal Prices.
The formal definition is that the Locational Marginal Price (LMP) at some node k in the network is the marginal cost to the RTO of delivering an additional unit of energy to node k. Relatedly, we sometimes define the "transmission price" or "congestion cost" between two nodes j and k in the network as the difference in LMPs between the two nodes.
The LMP forms the basis for payments to generators and payments by buyers in the PJM electricity market and other such markets in the US. Generators are paid the LMP at their node for electric energy produced, and buyers pay the LMP at their node for electric energy consumed. The RTO acts as the middleman for all purchases and sales, so it collects money from buyers and pays money to sellers.
If there is no transmission congestion in the network, then LMPs at all nodes are equal and will be equal to the System Marginal Price (SMP). This says that if no transmission lines are constrained, then the same marginal generator could be used to serve an additional unit of electric energy demand anywhere in the network.
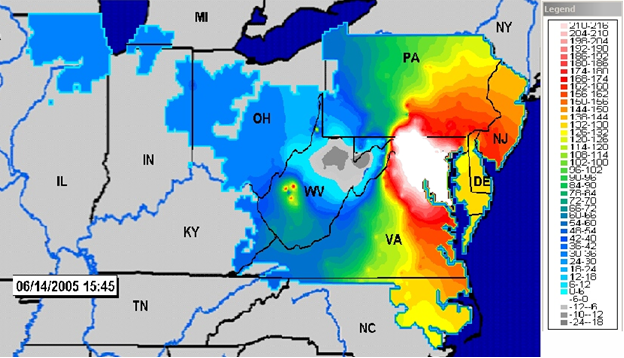
LMPs can be highly variable across different parts of an RTO territory and can be very volatile depending on system conditions. The figure below shows a heat map of LMPs in the PJM system on a warm, but not terribly hot, summer day. The areas in blue (in the western part of the PJM territory) have very low LMPs, indicating that there is a lot of low-cost generation capacity in those regions to meet demand. The areas in yellow and red exhibit higher LMPs, while the area around Washington, DC has the highest LMPs (in white). Why does this happen? The answer is that there are transmission constraints in the PJM network that limit the amount of low-cost generation in places like Ohio that can be used to meet high electricity demand in places like Washington, DC. There is plenty of generation but not enough transmission to move the power around. So to meet electricity demand in Washington, DC, PJM must use higher-cost generators that are located closer to Washington, DC.
Note that electricity demand is highly variable over time. Consequently, in addition to the high variability over the space, LMPs can also be highly variable over time.