11.10 How do these fluxes look?

11.10 How do these fluxes look?

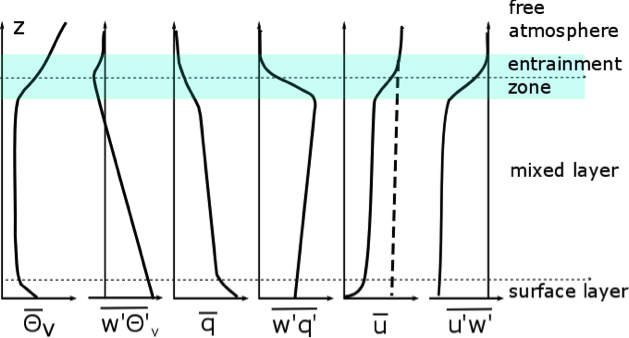
We have defined three mean variables, ${\overline{\theta }}_v$, $\overline{q}$, and $\overline{V_{}}$, and three eddy flux terms associated with these mean values, ${\overline{w\text{'}\theta \text{'}}}_v$, $\overline{w\text{'}q\text{'}}$, and $\overline{u\text{'}w\text{'}}$. Let’s examine their behavior as a function of height in the daytime boundary layer (see figure below).

The mean values and turbulent vertical fluxes of virtual potential temperature, specific humidity, and horizontal momentum for daytime conditions. The bottom solid line indicates the surface (z = 0). The top horizontal dashed line indicates the top of the boundary layer; the bottom horizontal dashed line indicates the top of the surface layer. The vertical dashed line is the calculated value of the geostrophic wind extending to the surface if there were no friction. The entrainment zone is an area of mixing between the mixed layer and the free atmosphere.

Credit: W. Brune, after Tennekes and Dreidonks, 1984

Virtual Potential Temperature, ${\overline{\theta }}_v$

The ${\overline{\theta }}_v$ profile is superadiabatic near the surface due to contact with the heated surface, neutral in the middle, and stable above. Eddies can rise from the surface to a height where ${\overline{\theta }}_v$ equals its surface value (assuming no cloud formation and condensation). The mixed layer will grow if surface heating or increased humidity by evaporation causes the surface ${\overline{\theta }}_v$ to increase, which means that air parcels can rise and be neutrally buoyant at greater ${\overline{\theta }}_v$ aloft and thus greater heights.

We see that the eddy flux ${\overline{w\text{'}\theta \text{'}}}_v$ is greatest at the surface, decreases nearly linearly with height, becomes slightly negative above the PBL height h because eddies are bringing warmer air down from above$\mathrm{}$. Remember, eddy fluxes carry a quantity like virtual potential temperature down the mean gradient. The eddy flux for virtual potential temperature (and all quantities) goes to very low values (essentially zero) above the entrainment zone even though a gradient is present because the eddy energy is much lower there.

Specific Humidity, $\overline{q}$

Specific humidity is greatest at the surface, where moisture sources, such as water bodies and vegetation, are present. The specific humidity falls off slowly with height until it reaches the PBL height, and then falls off rapidly into the free atmosphere. Because $\overline{q}$ falls off with height, the humidity flux $\overline{w\text{'}q\text{'}}$ is positive throughout the depth of the daytime ABL. Like all of the other turbulent fluxes, it is close to zero in the free troposphere becaue turbulence becomes weak and intermittent abouve the ABL. 

Horizontal Momentum Flux

$\overline{V_{}}$, the mean horizontal wind speed, increases logarithmically with height and then takes a jump above the PBL height as the wind no longer feels the friction from Earth’s surface and becomes geostrophic. The dashed line in the figure above indicates what the geostrophic wind would be without boundary layer friction. Because $\overline{V_{}}$is increasing with height, the horizontal momentum flux is negative throughout the boundary layer. It becomes less negative in the entrainment zone and approaches zero at heights above h.

So what does the daytime convective boundary layer look like? There are isolated convective updrafts surrounded by slower descending air, giving rise to the large-scale eddy circulation, as seen in the following video of the convective boundary layer, viewed from the top. Associated with the large eddies are smaller eddies that come about as the upward and downward air parcels move past each other. If you look closely, you will see eddies of all sizes in the video (:24), some quite large and some quite small, but the smaller ones seem to originate in the larger ones.