11.11 Turbulent Eddies: A Cascade of Energy
If an air parcel has a velocity, then it has kinetic energy. The air parcel's velocity can be broken down into average and perturbation parts and so can the kinetic energy. Now suppose we look at kinetic energy per volume of air: . Then we find the kinematic kinetic energy by dividing by the density.
If we start with the equation:
and we write each term as its mean and turbulent parts and then multiply all these terms out and take the Reynolds average, we can then apply the rules of averaging in Equation [11.1], and only two terms survive:
The first term is simply the kinetic energy associated with the mean wind. The second term is the kinetic energy associated with the turbulent wind and is called the turbulent kinetic energy, or TKE, for short.
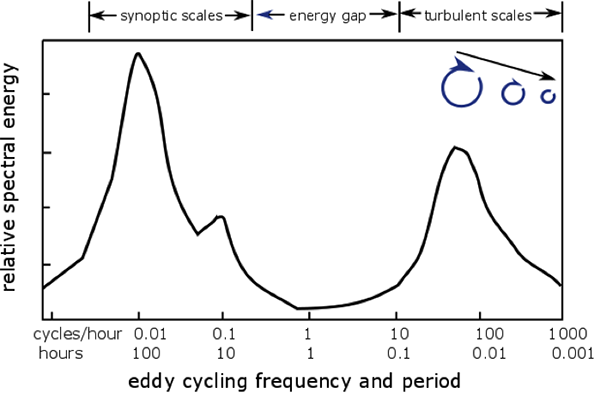
Which size eddies have the most energy? We can look at the relative intensity of the different scales of wind by considering the energy associated with motions of different sizes. Remember that, by the Taylor hypothesis, the size of an eddy observed by a stationary sensor and the period of the eddy are related by the speed with which the eddies are sampled, which is the mean wind at a stationary sensor. Large eddies will have longer periods and smaller eddies have smaller periods.
So, relative spectral intensity is just the amount of kinetic energy associated with that size eddy and the eddy size is associated with a period required for the eddy to pass over a sensor (see figure below).
- The peak in energy at 100 hours is from fronts and weather systems as they pass over a location. The spatial scale of these phenomena is relatively large and is called the synoptic scale.
- The smaller peak at about 24 hours is the diurnal cycle of wind speed, which increases during the day and then decreases at night.
- There is often a minimum in energy (called a spectral gap) at a time scale of an hour, where the circulations or eddies are relatively weak.
- This smaller peak at about 0.1 to 0.01 hours is called the “turbulent scale." This peak is caused by production of turbulent kinetic energy by buoyancy production (i.e., convection) and shear production (i.e., surface friction, the flux of momentum into Earth's surface). These eddies have the time scales of minutes and the size of the PBL.
- As the period of the eddies decreases below about 0.01 hours (about a minute), the strength of the eddies decreases.
- Eventually, on the subsecond time scale, the eddies have very little energy indeed.
Note that this figure is based on data taken close to Earth's surface. The peak energy at the turbulent scales will shift to lower frequencies and longer periods at greater heights above the surface. The maximum for ths "energy production scale" period is about 15 minutes and corresponds to convective eddies whose size is about as large as the depth of the daytime convective boundary layer. Turbulent energy production scales in the shallow stable nocturnal boundary layer are typically considerably smaller, with a maximum size that is about the depth of the noctural boundry layer, which is roughly 1/10th that of the daytime convective boundary layer.
So what is happening? Energy is flowing from the larger-scale eddies to the smaller-scale eddies. Eventually, the energy is dissipated through viscosity, which is a molecular-scale process. So, the energy of the larger eddies is transferred into smaller eddies, and eventually that energy is lost to viscosity, which in turn generates heating.
Lewis Richardson wrote a poem about this process for whorls (a.k.a. eddies) in 1922:
Big whorls have little whorls,
Which feed on their velocity;
And little whorls have lesser whorls,
And so on to viscosity
(in the molecular sense).