Simple Climate Models, cont'd

Gray Body Variant of the Zero Dimensional EBM

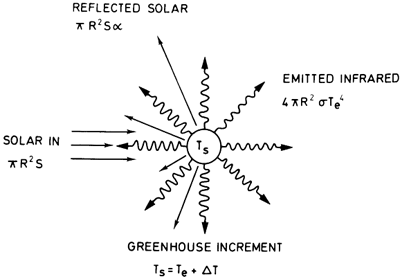
Even in the presence of the greenhouse effect, the net longwave radiation emitted out to space must balance the incoming absorbed solar radiation. So, we can think of the Earth system as still possessing an effective radiating temperature (T_e), which is the black body temperature we calculated earlier with the zero-dimensional EBM and the black body parameter values for A and B, i.e., T = 255^o K. It is the temperature Earth's surface has in the absence of any greenhouse effect. The outgoing longwave radiation to space is still given by $\epsilon \cdot \sigma \cdot {T_e}^4$. The atmosphere will have a temperature T_e somewhere aloft in the cooler region of the mid-troposphere. If we like, we can think of the Earth as, on average, emitting temperature to space from this level; hence, we refer to the temperature as the effective radiating temperature.

When a greenhouse effect is present, the temperature at the surface, T_S, will be substantially higher, however, due to the additional downward longwave radiation emitted by the atmosphere back down towards the Earth's surface.

We can attempt to account for this effect by simply changing the way we model the longwave radiation in the zero-dimensional EBM to account for the additional downward longwave radiation component.

Returning to the linearized form of the energy balance equation (i.e., equation (5) on the previous page), we will, therefore, now relax the assumption that A and B are given by their black body values. Instead, we will allow A and B to take on arbitrary values. This is a crude way of taking into account the fact that the Earth does not behave as a black body because the atmosphere has non-zero emissivity due to the presence of atmospheric greenhouse gases.

Simply put, we can tweak the values of A and B until they provide a good approximation. We refer to this generalized version of the black body approximation as the gray body approximation. The gray body model is a very crude way of accounting for the greenhouse effect in the context of a simple zero-dimensional model. In Lesson 5, we will build our way up to more realistic representations of the atmospheric greenhouse effect.

Various gray body parameter choices for A and B have been used by different researchers, in different situations. Since the gray body approximation is a linear approximation to a non-linear (Planck radiation) relationship, it is only valid over a limited range of temperatures about a given reference temperature. This means that a different set of parameters might be used for studying, e.g., the ice ages than would be used for studying, e.g., the early Cretaceous super greenhouse.

It turns out that the choices $A=214.4 W/m^2$ and $B=1.25 W/m^{2 }K{ }^{-1}$ yield realistic values for the current average temperature of the earth T_S, and gives a value for the climate sensitivity — a concept we will define in the next section — that is consistent with mid-range IPCC estimates. We will, therefore, adopt these as our standard gray body parameter values, but we will also explore the impact of using alternative values a bit later.

Figure 4.2: Simple Planetary Energy Balance - Greenhouse Effect Included.

Credit: Reprinted with permission from: A Climate Modeling Primer, A. Henderson-Sellers and K. McGuffie, Wiley, pg. 58, (1987).

The Concept of Equilibrium Climate Sensitivity

Let us rewrite the equation energy balance equation (5) on the previous page in a slightly different form,

where F_in represents the total incoming radiative energy flux at the surface, which includes incoming short wave radiation, but also any potential changes in the downward longwave radiation towards the surface.

Let us now consider the response of T_s to an incremental change in F_in. Since the 2nd term in (7) is a constant, we simply have

We can also rewrite (8) as

The change in downward longwave radiation forcing associated with a change in CO₂ concentration from a reference concentration, [CO₂]₀ to some new value, [CO₂], can be approximated by the following relationship from a paper by Myhre et al. (1998)

Now, let us further specify that we are interested in the change in radiative forcing resulting from a doubling of atmospheric CO₂ concentrations. For a CO₂ doubling, e.g., an increase from pre-industrial levels of 280 ppm to twice that value, 560 ppm,

We can define equilibrium climate sensitivity, s, as the change in temperature resulting from a doubling of pre-industrial CO₂ concentrations; s has units of K (or equivalently degrees C, since differences in C and K are equal). To estimate s, we combine equations (8) and (11)

The equilibrium climate sensitivity is the equilibrium warming we expect in response to CO₂ doubling. In the simple case of the 0d EBM, it is readily calculated through equation (12).