Lesson 5: Translating the coordinate system

New syntax introduced: translate(), pushMatrix(), popMatrix()

You know that the default coordinate system has (0,0) in the upper left corner and increases to the right and downwards. You can change this system by calling the function translate(). The translate() function takes two arguments: the number of pixels added to x and the number of pixels added to y. All shapes drawn after translate() will adhere to the new coordinate structure.

The tricky thing to remember about translation is that you aren't really moving the shapes you draw. Instead you are moving the entire coordinate system relative to the display window. Consider the hand-drawn sketch below in which there is a heart whose top cusp is at (3,2), shown by the black dot.

Red heart on graph paper

E. Richardson

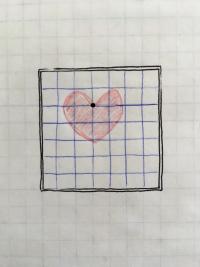
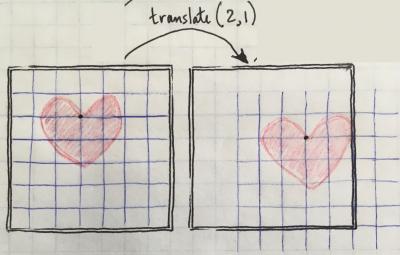
Now if I translate the coordinate system 2 over and 1 down, the display window stays where it is and the heart stays where it is relative to the coordinate mesh, but the coordinate mesh itself has been shifted. So in pseudo-code this would be like:

translate(2,1);

heart(3,2);

Heart translated two units to the right and one unit down.

E. Richardson

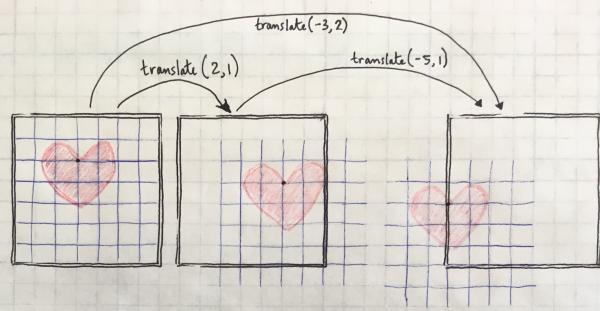
Translations are cumulative, so the third panel can be achieved either by translating (-5,1) from the second panel, or by translating (-3,2) directly from the first panel. If we had really drawn the third version in Processing, you'd only see the right half of the heart because the other side is out of the display window. Philosophers can tell us whether it exists or not, but in any case we can't see it.

So in pseudo-code this would be:

translate(2,1);

translate(-5,1);

heart(3,2);

Or it could have been

translate(-3,2);

heart(3,2);

Note how I'm always drawing the heart itself with the same coordinates it had in the first place.

Another translation. Either (-5,1) from the second position, or (-3,2) from the original position.

E. Richardson

Example 5.6

Here is an example in an actual program. Notice in this program that rectangle is always specified by the same coordinates. You can see how translation is cumulative and can be negative, too.

// Demonstrate Translation

size(200, 200);
rect(10, 10, 50, 20); // Draw a rectangle 
translate(100, 100);  // Move the origin to (100, 100)
rect(10, 10, 50, 20); // Draw the same rectangle, but now it is shifted
translate(50, 50);    // Move the origin to (150, 150)
rect(10, 10, 50, 20); // Same rectangle shifted more
translate(0, -75);    // Translations can be negative
fill(255, 0, 0);    
rect(10, 10, 50, 20); // Same rectangle shifted up and colored red

Example of cumulative and negative translation

E. Richardson

To change the coordinate system temporarily and then have it go back to the way it was before you made a transformation without having to manually make a negative translation, use pushMatrix() and popMatrix(). These functions always have to be used together. The way it works is that you stick in a pushMatrix() before you write the transformation and then you stick in a popMatrix() just before you want to revert back. The coordinate system will revert back to the way it was before pushMatrix().

Example 5.7

// Use pushMatrix and popMatrix to revert the translation

size(200, 200);

pushMatrix();

for (int i = 1; i < 200; i++) {
   translate(i, i);
   rect(1, 1, 50, 20); // Draw a rectangle
}

popMatrix();
ellipse(100, 100, 20, 20);

Demonstration of pushMatrix() and popMatrix().

E. Richardson

Note how in the code in Example 5.7 the circle draws in the center of the screen because the for loop was enclosed by a pushMatrix() popMatrix() pair, meaning that all those accumulated translations didn’t affect the circle.