Elevation Factor

Elevation Factor

Source: GPS for Land Surveyors

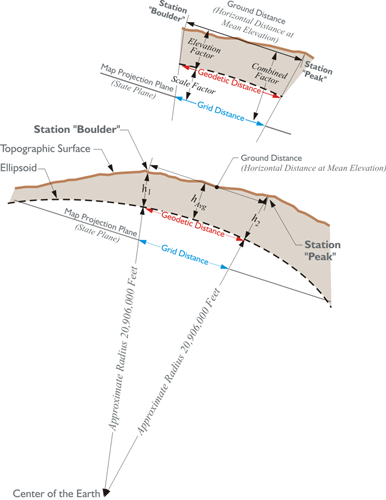
But, that is not the whole story when it comes to reducing distance to the State Plane Coordinate grid. Measurement of lines must always be done on the topographic surface of the Earth, and not on the ellipsoid. Therefore, the first step in deriving a grid distance must be moving a measured line from the Earth to the ellipsoid. The scale factor moves us from the ellipsoid to the state plane (aka grid). However, as mentioned here, the measurements are not made on the ellipsoid. They are made on the surface of the Earth. If we're going to measure the line from one point to another — from station Boulder to station Peak as shown in the illustration— that distance would be measured on the surface of the Earth. To move from the surface of the Earth down to the ellipsoid, we need to have what's known as an elevation factor. Typically, the elevation factor for a line is the average of the elevation factors at each end of the line. For example, the average of the elevation factor at station Boulder (h₁), and the elevation factor at station Peak (h₂) is the elevation factor for the line (h_Avg). That would give the elevation factor for the line Boulder-Peak. Once the elevation factor is available, it is multiplied with the scale factor. The result is known as the combined factor. The combined factor will move the line from the topographic surface of the Earth to the state plane (aka grid).

In the illustration, you may have noticed the approximate radius of the Earth, 20,906,000 feet. It is shown from the center of mass of the Earth up to the ellipsoid. It is an approximation used in creating this elevation factor.

In other words, converting a distance measured on the topographic surface to a geodetic distance on the reference ellipsoid is done with another ratio that is also used as a multiplier. Originally, this factor had a rather unfortunate name. It used to be known as the sea level factor in SPCS27. It was given that name because as you may recall that when NAD27 was established using the Clarke 1866 reference ellipsoid, the distance between the ellipsoid and the geoid was declared to be zero at Meades Ranch in Kansas. That meant that in the middle of the country the sea level surface, the geoid, and the ellipsoid were coincident by definition. And since the Clarke 1866 ellipsoid fit the United States quite well, the separation between the two surfaces, the ellipsoid and geoid, only grew to about 12 meters anywhere in the country. With such a small distance between them, many practitioners at the time took the point of view that, for all practical purposes, the ellipsoid and the geoid were in the same place. And that place was called sea level. Hence, reducing a distance measure on the surface of the Earth to the ellipsoid was said to be reducing it to sea level.

Today, that idea and that name for the factor are misleading because, of course, the GRS80 ellipsoid on which NAD83 is based is certainly not the same as Mean Sea Level. The separation between the geoid and ellipsoid can grow as large as 53 meters. And technology by which lines are measured has improved dramatically. Therefore, in SPCS83, the factor for reducing a measured distance to the ellipsoid is known as the ellipsoid factor. In any case, both the old and the new name can be covered under the name the elevation factor. Regardless of the name applied to the factor, it is a ratio. The ratio is the relationship between an approximation of the Earth’s radius and that same approximation with the mean ellipsoidal height of the measured line added to it. For example, consider station Boulder and station Peak illustrated in the figure above. 

Boulder

• N39º59’29.1299”
• W105º15’39.6758”

Peak

• N40º01’19.1582”
• W105º30’55.1283”

The distance between these two stations is 72,126.21 feet. This distance is sometimes called the ground distance, or the horizontal distance at mean elevation. In other words, it is not the slope distance but rather the distance between them corrected to an averaged horizontal plane, as is common practice. For practical purposes, then, this is the distance between the two stations on the topographic surface of the Earth. On the way to finding the grid distance Boulder to Peak, there is the interim step, calculating the geodetic distance between them, that is the distance on the ellipsoid. We need the elevation factor, and here is how it is determined.

The ellipsoidal height of Boulder, h₁, is 5,437 feet. The ellipsoidal height of Peak, h₂, is 9,099 feet. The approximate radius of the Earth, traditionally used in this work, is 20,906,000 feet. The elevation factor is calculated:

$$ElevationFactor=\mathrm{R/}R+\mathrm{h(average)}$$  $$ElevationFactor=20,906,000ft./20,906,000+7,268ft.$$$$ElevationFactor=20,906,000ft./20,913,268ft.$$$$ElevationFactor=0.99965247$$

This factor then is the ratio used to move the ground distance down to the ellipsoid, down to the geodetic distance.

$$GroundDistanceBouldertoPeak=72,126.21ft.$$

$$$$ $$GeodeticDistance=GroundDistance\ast ElevationFactor$$

$$$$ $$GeodeticDistance=72,126.21\ast 0.99965247$$

$$$$ $$GeodeticDistance=72,101.14ft.$$

It is possible to refine the calculation of the elevation factor by using an average of the actual radial distances from the center of the ellipsoid to the end points of the line, rather than the approximate 20,906,000 feet. In the area of stations Boulder and Peak, the average ellipsoidal radius is actually a bit longer, but it is worth noting that within the continental United States such variation will not cause a calculated geodetic distance to differ significantly.