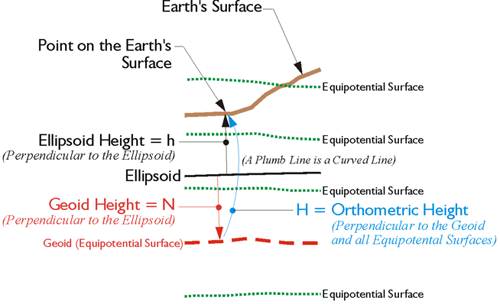
A geoidal height is the distance measured along a line perpendicular to the ellipsoid of reference to the geoid. Also, as you can see in the illustration, these geoid heights are negative. They are usually symbolized, N. If the geoid is above the ellipsoid, N is positive; if the geoid is below the ellipsoid, N is negative. It is negative here because the geoid is underneath the ellipsoid throughout the conterminous United States. In Alaska, it is the other way around; the ellipsoid is underneath the geoid and N is positive.
Please recall that an ellipsoid height is symbolized, h. The ellipsoid height is also measured along a line perpendicular to the ellipsoid of reference, but to a point on the surface of the Earth.
However, an orthometric height, symbolized, H, is measured along a plumb line from the geoid to a point on the surface of the Earth. By using the formula,
H = h – N
one can convert an ellipsoidal height, h, derived say from a GPS/GNSS observation, into an orthometric height, H, by knowing the extent of geoid-ellipsoid separation, also known as the geoidal height, N, at that point. The ellipsoid height of a particular point is actually smaller than the orthometric height throughout the conterminous United States.
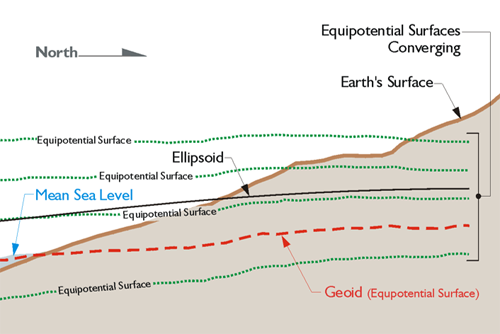
The formula H = h – N does not account for the fact that the plumb line along which an orthometric height is measured is curved, as you see in the figure above. Curved, because it is perpendicular with each and every equipotential surface through which it passes. The equipotential surfaces are not parallel with each other. They converge toward the pole because the Earth is oblate therefore, the plumb line must curve to maintain perpendicularity with them all. This deviation of a plumb line from the perpendicular to the ellipsoid reaches about 1 minute of arc in only the most extreme cases. Therefore, any height difference that is caused by the curvature is negligible. It would take a height of over 6 miles for the curvature to amount to even 1 mm of difference in height.