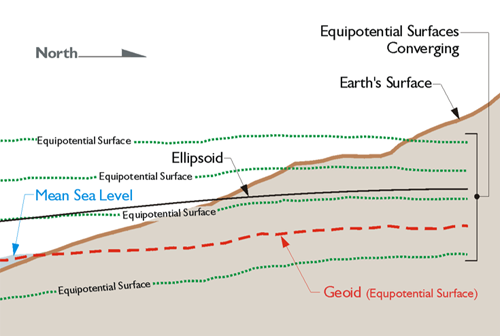
Any object in the earth’s gravitational field has potential energy derived from being pulled toward the Earth. Quantifying this potential energy is one way to talk about height, because the amount of potential energy an object derives from the force of gravity is related to its height. There are an infinite number of points where the potential of gravity is always the same. They are known as equipotential surfaces. Mean Sea Level itself is not an equipotential surface at all, of course. Forces other than gravity affect it, forces such as temperature, salinity, currents, wind, and so forth. The geoid, on the other hand, is defined by gravity alone. The geoid is the particular equipotential surface arranged to fit Mean Sea Level as well as possible, in at least squares sense. The geoid and the ellipsoid are not the same. Remember that the legacy heights determined by optical instruments in the past were always relative to the geoid, because, of course, the instruments were oriented to gravity. However, GPS/GNSS heights are related directly at least to the ellipsoid —two different surfaces.
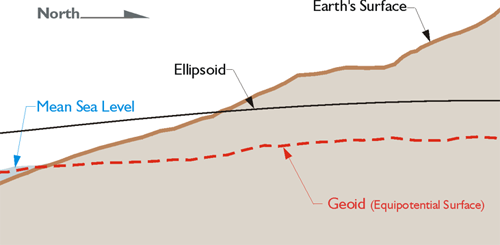
So, while there is a relationship between Mean Sea Level and the geoid, they are not the same. They could be the same if the oceans of the world could be utterly still, completely free of currents, tides, friction, variations in temperature, and all other physical forces, except gravity. However, these unavoidable forces actually cause Mean Sea Level to deviate up to 1, even 2, meters from the geoid.
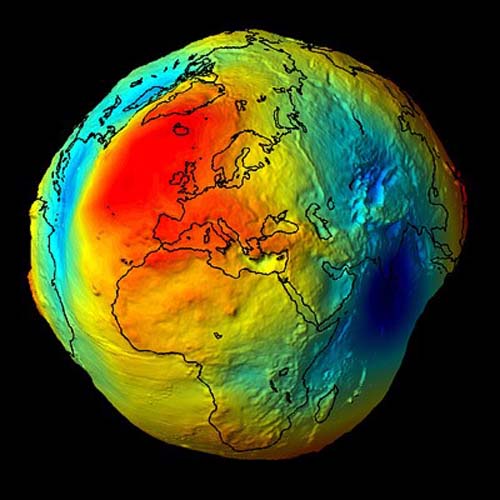
The geoid is completely is not smooth and continuous. It is lumpy, because gravity is not consistent across the surface of the earth. At every point, gravity has a magnitude and a direction, but these vectors do not all have the same direction or magnitude. Some parts of the earth are denser than others. Where the earth is denser, there is more gravity, and the fact that the earth is not a sphere also affects gravity. The geoid undulates with the uneven distribution of the mass of the earth and has all the irregularity that the attendant variation in gravity implies. In fact, the separation between the lumpy surface of the geoid and the smooth GRS80 ellipsoid worldwide varies from about +85 meters west of Ireland to about -106 meters, the latter in the area south of India near Ceylon.
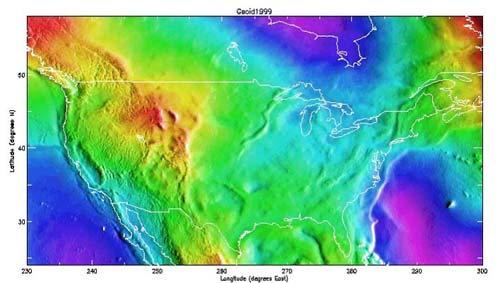
In the conterminous United States, sometimes-abbreviated CONUS, the distances between the geoid and the GRS80 ellipsoid, known as geoid heights, are less. They vary from about –8 meters to about –53 meters.