METEO 300
Fundamentals of Atmospheric Science

6.3 How is energy related to the wavelength of radiation?

PrintPrint

6.3 How is energy related to the wavelength of radiation?

We can think of radiation either as waves or as individual particles called photons. The energy associated with a single photon is given by E = hν , where E is the energy (SI units of J), h is Planck's constant (h = 6.626 x 10–34 J s), and ν is the frequency of the radiation (SI units of s–1 or Hertz, Hz) (see figure below). Frequency is related to wavelength by λ=c/ν , where c, the speed of light, is 2.998 x 108 m s–1. Another quantity that you will often see is wavenumber, σ=1/λ, which is commonly reported in units of cm–1.

The energy of a single photon that has the wavelength λ is given by:

E =  hc λ =  1.986×  10 −16  J nm photon −1 λ MathType@MTEF@5@5@+=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCaerbdfwBIjxAHbqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaabauaaaOqaaabbaaaaaaaaIXwyJTgapeGaamyraiaabckacqGH9aqpcaqGGcWaaSaaaeaacaWGObGaam4yaaqaaiabeU7aSbaacqGH9aqpcaqGGcWaaSaaa8aabaWdbiaaigdacaGGUaGaaGyoaiaaiIdacaaI2aGaey41aqRaaeiOaiaaigdacaaIWaWdamaaCaaaleqabaWdbiabgkHiTiaaigdacaaI2aaaaOGaaeiOaiaabQeacaqGGaGaaeOBaiaab2gacaqGGcGaaeiCaiaabIgacaqGVbGaaeiDaiaab+gacaqGUbWdamaaCaaaleqabaWdbiabgkHiTiaaigdaaaaak8aabaWdbiabeU7aSbaaaaa@5AA2@

[6.2a]

Note that as the wavelength of light gets shorter, the energy of the photon gets greater. The energy of a mole of photons that have the wavelength λ is found by multiplying the above equation by Avogadro's number:

E m  =  hc N A λ =  1.196 ×  10 8  J nm mol −1 λ MathType@MTEF@5@5@+=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCaerbdfwBIjxAHbqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaabauaaaOqaaabbaaaaaaaaIXwyJTgapeGaamyra8aadaWgaaWcbaWdbiaad2gaa8aabeaak8qacaqGGcGaeyypa0JaaeiOamaalaaabaGaamiAaiaadogacaWGobWdamaaBaaaleaapeGaamyqaaWdaeqaaaGcpeqaaiabeU7aSbaacqGH9aqpcaqGGcWaaSaaa8aabaWdbiaaigdacaGGUaGaaGymaiaaiMdacaaI2aGaaeiOaiabgEna0kaabckacaaIXaGaaGima8aadaahaaWcbeqaa8qacaaI4aaaaOGaaeiiaiaabQeacaqGGaGaaeOBaiaab2gacaqGGcGaaeyBaiaab+gacaqGSbWdamaaCaaaleqabaWdbiabgkHiTiaaigdaaaaak8aabaWdbiabeU7aSbaaaaa@5A32@

[6.2b]
 
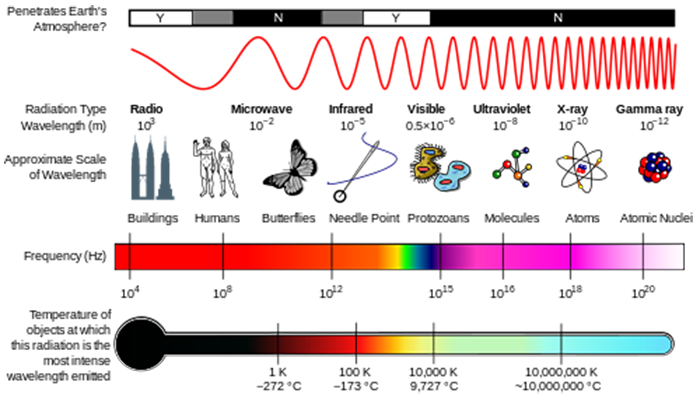
wave size-radio: building, microwave: butterfly, infrared: needle, visible: protazoa, ultraviolet: molecule, x-ray: atoms, gamma: nucleus
Energy scales: penetration through Earth’s atmosphere; radiation name by wavelength; physical object the size of that wavelength; frequency compared to wavelength; and temperature of an object that has its peak radiation at each wavelength.
Credit: Credit: EM Spectrum Properties reflected by Inductiveload from Wikimedia Commons is licensed under CC BY-SA 3.0.

In the lesson on atmospheric composition, you saw how solar UV radiation was able to break apart molecules to initiate atmospheric chemistry. These molecules are absorbing the energy of a photon of radiation, and if that photon energy is greater than the strength of the chemical bond, the molecule may break apart.

Check Your Understanding

Consider the reaction O3 + UV → O2 + O*. If the bond strength between O2 and O* (i.e., excited state oxygen atom) is 386 kJ mol–1, what is the longest wavelength that a photon can have and still break this bond?

Click for answer.

ANSWER: Solve for wavelength in equation [6.2b]

λ=  1.196 ×  10 8  J nm mol −1 E m  = 1.196 ×  10 8  J nm mol −1 386 ×  10 3  J mol −1 =309 nm MathType@MTEF@5@5@+=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCaerbdfwBIjxAHbqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaabauaaaOqaaabbaaaaaaaaIXwyJTgapeGaeq4UdWMaeyypa0JaaeiOamaalaaapaqaa8qacaaIXaGaaiOlaiaaigdacaaI5aGaaGOnaiaabckacqGHxdaTcaqGGcGaaGymaiaaicdapaWaaWbaaSqabeaapeGaaGioaaaakiaabckacaqGkbGaaeiOaiaab6gacaqGTbGaaeiOaiaab2gacaqGVbGaaeiBa8aadaahaaWcbeqaa8qacqGHsislcaaIXaaaaaGcpaqaa8qacaWGfbWdamaaBaaaleaapeGaamyBaaWdaeqaaaaak8qacaqGGcGaeyypa0ZaaSaaa8aabaWdbiaaigdacaGGUaGaaGymaiaaiMdacaaI2aGaaeiOaiabgEna0kaabckacaaIXaGaaGima8aadaahaaWcbeqaa8qacaaI4aaaaOGaaeiOaiaabQeacaqGGcGaaeOBaiaab2gacaqGGcGaaeyBaiaab+gacaqGSbWdamaaCaaaleqabaWdbiabgkHiTiaaigdaaaaak8aabaWdbiaaiodacaaI4aGaaGOnaiaabckacqGHxdaTcaqGGcGaaGymaiaaicdapaWaaWbaaSqabeaapeGaaG4maaaakiaabckacaqGkbGaaeiOaiaab2gacaqGVbGaaeiBa8aadaahaaWcbeqaa8qacqGHsislcaaIXaaaaaaakiabg2da9iaaiodacaaIWaGaaGyoaiaabckacaqGUbGaaeyBaaaa@817C@