6.12 What about scattering?
Besides being absorbed or transmitted, radiation can be scattered. The scattering can be by particles of all sizes and by molecules. We can talk about the extinction of radiation by a particle that both absorbs and scatters.
When we have absorption and scattering by particles or molecules, we simply replace the absorption cross section with the extinction cross section in Equations 6.9 to 6.13 (see section 6.10).
Scattering is messy!!!! While absorption simply removes photons, or energy, from a beam of radiation, scattering can redirect the beam of radiation into other directions, where it can be absorbed or scattered some more. Furthermore, the intensity of the scattered radiation in different directions depends strongly on the radiation's wavelength and on the size, shape, and composition of the “particle,” where we can consider a molecule to be a particle.
A very important parameter is called the size parameter:
where r is the radius of a spherical particle and λ is the radiation’s wavelength.
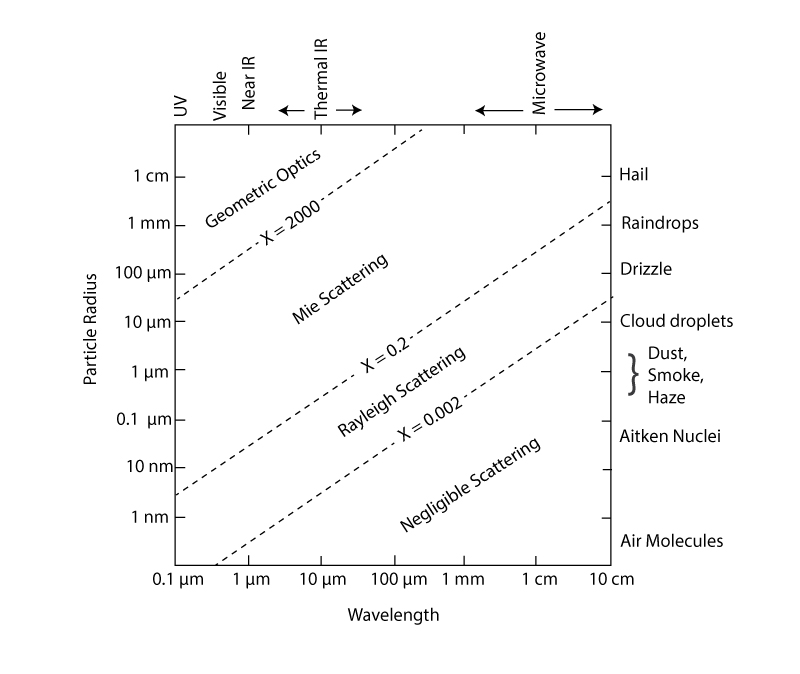
The effectiveness of scattering depends on the size parameter, which separates different types of scattering. For x > 2000, we have geometric optics. Geometric optics is when the particles get so big relative to the wavelength that we can calculate the interaction of radiation with them using optical principles (think of a lens or prism). For x = 0.2 to 2000, we have Mie scattering. Mie scattering is when the particle size is comparable to the size of the radiation wavelength, such as many atmospheric particles and light, from UV to microwave. For x between 0.002 and 0.2, we have Rayleigh scattering. Rayleigh scattering occurs for particles that are smaller than the radiation’s wavelength. This is the regime for molecules for the UV into the visible and for drizzle and raindrops for radar. Let’s look at its properties.
Without going through the math or the reasoning, I will state only that the scattering cross section for a molecule, particle, or raindrop in the Rayleigh regime (x << 1) is proportional to the sixth power of the particle radius and fourth power of the radiation wavelength.
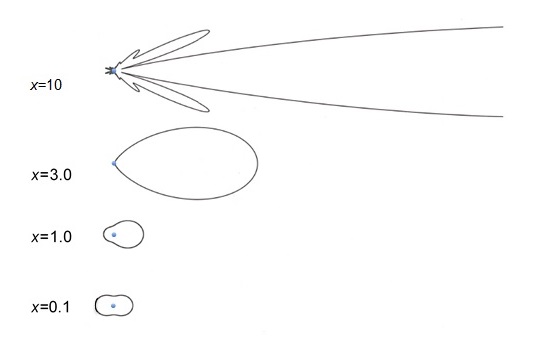
In the Rayleigh regime, this scattering is equally strong in the backward and forward directions, with slightly less scattering in other directions (see figure above).
This strong wavelength dependence of scattering by small particles includes molecules at the wavelengths of visible radiation. This wavelength dependence of scattering leads to the preferential scattering of blue solar radiation compared to red solar radiation, which contributes to the blue of the sky in directions away from the sun and the deep orange-to-red colored sun as it sets. The image below shows both effects in one picture—a yellow-orange sunset below the cloud and a bright blue sky above the cloud.
For radar wavelengths, the r6 dependence of scattering by cloud and rain drops leads to much stronger back scattering of the radar beam with increasing drop size, thus allowing for estimates of raindrop sizes and thus rainfall rates.

See below for a video (2:09) explaining scattering in greater depth:
Scattering is messy. So we will focus on just a few concepts that you can use. The first is the concept of size parameter, which is just two pi times the molecule or particle radius divided by the radiation wavelength. The graph of the particle radius and wavelengths with different size parameters begins to make more sense when we talk about how different size parameters affect scatter. This figure on scattering patterns for different size parameters illustrates the importance of the size parameter. For size parameters one and above, that is the particle radius more than 1/6 of the radiation wavelength, we see that the radiation is strongly scattered in the forward direction, with little radiation scattered to the back or side. When the radiation wavelengths is much larger than the particle radius, the more the radiation is scattered back toward the radiator source into the side. This should give you some idea how the radiation wavelength which shows up on radar, which looks at the back scattered radiation for precipitation. Note that the most efficient scattering of radiation occurs when the particle radius is about equal to the radiation wavelength, and that for radiation with much shorter wavelengths, scattering is inefficient, while the scattering for radiation with longer wavelengths is almost as small. Last, we should look at the [INAUDIBLE] of the scattering cross section of particle radius and radiation wavelength. For small size parameters, the scattering cross section, which is just a scattering strength, is proportional to the particle radius to the sixth power and the inverse of the radiation wavelength to the fourth power. Equation 619 tells us that blue radiation is scattered much better than red radiation. And quite a bit of the radiation is scattered to the side. In fact, this more efficient scattering of blue is part of the reason that the sky is blue, but that the sun appears to be yellow when high in the sky, and even red when setting.
Quiz 6-4: Scatter brained
When you feel you are ready, take Quiz 6-4. You will be allowed to take this quiz only once. Good luck!