METEO 300
Fundamentals of Atmospheric Science

6.10 How much radiation is absorbed as radiation passes through matter?

PrintPrint

6.10 How much radiation is absorbed as radiation passes through matter?

Gases, liquids, and solids can all absorb radiation. Since we are most interested in gases, we will use a gas to develop the equation that we need for absorption.

Suppose we have a volume of uniformly distributed gas that absorbs. Let's suppose that there is a beam of radiation that passes into this medium. Let's narrow this beam down so that all the radiation is traveling in essentially the same direction, so now we are interested in the irradiance that is traveling in a narrow range of angles, which is called the radiance, which is denoted by I and has units of W m–2 steradian–1 nm–1. Refer back to Lesson 6.5 to refresh your memory about what steradians are.

In an infinitesimal slab of that medium, a certain fraction dI of the radiation with radiance I (W m–2) is absorbed. dI is equal to the absorption cross section, σ (m2), of a single molecule or particle multiplied by the number density, n (# m–3) of absorbers, the length of the light-path through the slab, ds (m), and the amount of radiance I itself :

dI( λ )=−I( λ )σ( λ )nds
[6.9]

Note that both I and σ are functions of wavelength. If there is a beam of radiation with a certain wavelength, then the chance of absorbing the radiation depends on the cross-sectional area of each molecule or particle, which quantifies the efficiency with which the molecule absorbs the radiation with that particular wavelength. The absorption cross sections are largest if the energy of the radiation's wavelength matches the transition energy of an electron, atom, or molecule.

Integrating this expression over the total thickness of the volume, we get the Beer–Lambert Law:

I( λ )= I o ( λ )exp[ −σ( λ )ns ] MathType@MTEF@5@5@+=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCaerbdfwBIjxAHbqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaabauaaaOqaaabbaaaaaaaaIXwyJTgapeGaamysamaabmaapaqaa8qacqaH7oaBaiaawIcacaGLPaaacqGH9aqpcaWGjbWdamaaBaaaleaapeGaam4BaaWdaeqaaOWdbmaabmaapaqaa8qacqaH7oaBaiaawIcacaGLPaaaciGGLbGaaiiEaiaacchadaWadaqaaiabgkHiTiabeo8aZnaabmaapaqaa8qacqaH7oaBaiaawIcacaGLPaaacaWGUbGaam4CaaGaay5waiaaw2faaaaa@4DF0@

[6.10]

where Io is the radiance at the front edge of the path and I is the radiance at distance s along the path. Sometimes, we substitute a variable κa, called the absorption coefficient, for the product σn. In fact, you will see the absorption coefficient reported many ways.

When σns = 1, I(λ)/Io(λ) = exp(–1) = 0.368.

For a uniform gas, the optical depth equals σns and is often given by the symbol τ (tau). If the optical depth gets large, then very little radiation gets through.

light shining into beaker of pink liquid
Example of Beer–Lambert Law: Laser light shining into a solution of a dye (Rhodamine 6B), which converts the green radiation to yellow radiation by a process called fluorescence. The yellow beam becomes weaker as it passes through solution because the green radiation that is making the dye fluoresce is being absorbed according to the Beer–Lambert Law.
Credit: Wikipedia

Check Your Understanding

Ozone has an absorption cross section of 1.0 x 10–19 cm2 at a wavelength of 310 nm. If the average ozone concentration in the ozone layer is 2 x 1012 molecules cm–3 and the thickness of the ozone layer is 25 km, what is the fraction of sunlight that gets through when the sun is directly overhead?

Click for answer.

ANSWER:

I( λ ) I o ( λ ) =exp( –1× 10 −19 cm 2 ⋅2× 10 12 cm −3 ⋅25× 10 5 cm )=0.6 MathType@MTEF@5@5@+=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCaerbdfwBIjxAHbqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaabauaaaOqaaabbaaaaaaaaIXwyJTgapeWaaSaaa8aabaWdbiaadMeadaqadaWdaeaapeGaeq4UdWgacaGLOaGaayzkaaaapaqaa8qacaWGjbWdamaaBaaaleaapeGaam4BaaWdaeqaaOWdbmaabmaapaqaa8qacqaH7oaBaiaawIcacaGLPaaaaaGaeyypa0JaciyzaiaacIhacaGGWbWaaeWaaeaacaaIXaGaey41aqRaaGymaiaaicdapaWaaWbaaSqabeaapeGaeyOeI0IaaGymaiaaiMdaaaGcpaGaae4yaiaab2gadaahaaWcbeqaaiaaikdaaaGccqGHflY1peGaaGOmaiabgEna0kaaigdacaaIWaWdamaaCaaaleqabaWdbiaaigdacaaIYaaaaOWdaiaabogacaqGTbWaaWbaaSqabeaacqGHsislcaaIZaaaaOGaeyyXIC9dbiaaikdacaaI1aGaey41aqRaaGymaiaaicdapaWaaWbaaSqabeaapeGaaGynaaaak8aacaqGJbGaaeyBaaWdbiaawIcacaGLPaaacqGH9aqpcaaIWaGaaiOlaiaaiAdacaaIWaaaaa@6A4A@

At 310 nm, 60% of the solar UV gets through to Earth’s surface. Yet at 290 nm, where σ = 1.09 x 10–18 cm2, only 0.4% of the solar UV gets through.

Once we know the absorption coefficients of all of the absorbing molecules between the sun and the air volume of interest and the number densities of the absorbers, we can determine how much radiation will be absorbed at every wavelength.

The angle of the Sun with respect to the zenith (directly overhead) is called the solar zenith angle (SZA) and is 0o overhead and 90o on the horizon. The SZA affects the total path through absorbers, and thus is important. We often make an assumption that the atmosphere is a parallel plane (see figure below).

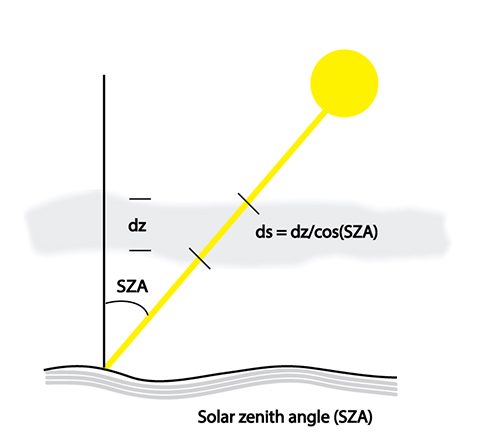
Schematic of the increase in path length with solar zenith angle as solar radiation passes through a layer
Schematic of the increase in path length with solar zenith angle as solar radiation passes through a layer, since ds > dz.

The result is that we can write ds= 1 cos SZA dz=sec SZA dz in the differential form of Beer's Law:

dI( λ ) I( λ ) =−σ( λ )n sec( SZA )dz MathType@MTEF@5@5@+=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCaerbdfwBIjxAHbqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaabauaaaOqaaabbaaaaaaaaIXwyJTgapeWaaSaaa8aabaWdbiaadsgacaWGjbWaaeWaa8aabaWdbiabeU7aSbGaayjkaiaawMcaaaWdaeaapeGaamysamaabmaapaqaa8qacqaH7oaBaiaawIcacaGLPaaaaaGaeyypa0JaeyOeI0Iaeq4Wdm3aaeWaa8aabaWdbiabeU7aSbGaayjkaiaawMcaaiaad6gacaqGGaGaae4CaiaabwgacaqGJbWaaeWaa8aabaWdbiaabofacaqGAbGaaeyqaaGaayjkaiaawMcaaiaadsgacaWG6baaaa@5168@

[6.11]

which gives:

I( λ,z )= I 0 ( λ )exp[ −sec( SZA ) ∫ ​ σ( λ )n( z )dz ] MathType@MTEF@5@5@+=faaagCart1ev2aaaKnaaaaWenf2ys9wBH5garuavP1wzZbItLDhis9wBH5garmWu51MyVXgaruWqVvNCPvMCaerbdfwBIjxAHbqee0evGueE0jxyaibaieYlf9irVeeu0dXdh9vqqj=hHeeu0xXdbba9frFj0=OqFfea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr0=vqpi0dc9GqpWqaaeaabiGaciaacaqabeaadaabauaaaOqaaabbaaaaaaaaIXwyJTgapeGaamysamaabmaapaqaa8qacqaH7oaBcaGGSaGaamOEaaGaayjkaiaawMcaaiabg2da9iaadMeapaWaaSbaaSqaa8qacaaIWaaapaqabaGcpeWaaeWaa8aabaWdbiabeU7aSbGaayjkaiaawMcaaiGacwgacaGG4bGaaiiCamaadmaabaGaeyOeI0Iaae4CaiaabwgacaqGJbWaaeWaa8aabaWdbiaabofacaqGAbGaaeyqaaGaayjkaiaawMcaa8aadaqfGaqabSqabeaacaaMb8oaneaapeGaey4kIipaaOGaeq4Wdm3aaeWaa8aabaWdbiabeU7aSbGaayjkaiaawMcaaiaad6gadaqadaWdaeaapeGaamOEaaGaayjkaiaawMcaaiaadsgacaWG6baacaGLBbGaayzxaaaaaa@5DB3@

[6.12]

Often, the integral is called the optical thickness, or optical path, where s1 is one point along the path and s2 is another. The exponential of the optical thickness, factoring in the sec(SZA), equals exp[–sec(SZA) τ(s1,s2)] and is called the transmittance, often designated with the symbol t, where τ is the optical depth.

τ( s 1 , s 2 )≡ ∫ s 1 s 2 σ(s)⋅n(s)⋅ds This equation is not rendering properly due to an incompatible browser. See Technical Requirements in the Orientation for a list of compatible browsers.

[6.13]

For matter that absorbs and does not scatter, the absorptivity, a = 1 – t. Note that in this case the emissivity ε = a = 1 – t.

Usually, but not always, σ is a function of altitude because it often is a function of pressure and temperature, which vary for different altitudes.

Here is a video (2:03) further explaining Beer's Law:

Beer's Law
Click here for transcript of the Beer's Law video.

The absorption of radiation can be described by the Beer-Lambert law, sometimes just called Beer's law. Note that any change to the radiance equals the product of the amount of radiance, the absorption cross-section of matter, whether they be atoms or molecules, through which the radiation is passing, the number concentration of the absorbing molecules or atoms, and the path length. Note that this cross-section is wavelength-dependent and may be pressure and temperature-dependent as well. You should be able to easily integrate this equation to get the exponential form of Beer's law. Remember that e to the minus 1 is just 0.37, only about 1/3 left. e to the minus 2 is just 0.13. In the example photograph, the green laser is shining into a dye solution that absorbs the green laser radiation and then fluoresces in the yellow color. As the green radiation penetrates further into the dye solution, more of it gets absorbed and less gets transmitted, until we see that there is too little green radiation left to make the dye solution fluoresce. With the atmosphere, the absorbers are often arranged in atmospheric layers. The stratospheric ozone layer is one example. In this case, the layer thickness is called dz. For sun directly overhead, the path length through the layer is a minimum, which means that the greatest amount of radiation should be able to pass through. However, as the sun is at higher solar zenith angles, where the solar zenith angle is the angle from the vertical, then the path length through the layer increases, so we would expect more absorption. And because the decrease in radiation is exponential with path length, we should expect the amount of radiation absorbed at high solar zenith angles be great compared to the case of the overhead sun.