6.7 What is the total irradiance of any object?
If the Planck distribution function spectral irradiance is integrated over all wavelengths, then the total irradiance emitted into a hemisphere is given by the Stefan–Boltzmann Law:
where σ is called the Stefan–Boltzmann constant (5.67 x 10–8 W m–2 K–4). Fs has SI units of W m–2, where the m2 refers to the surface area of the object that is radiating.
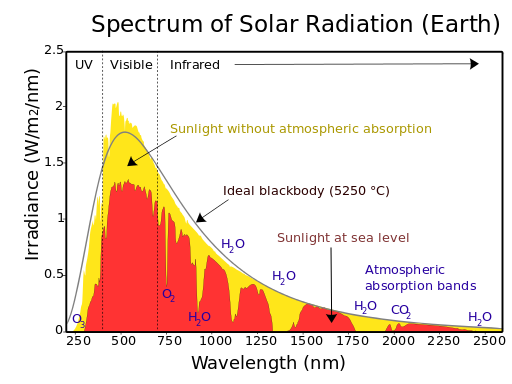
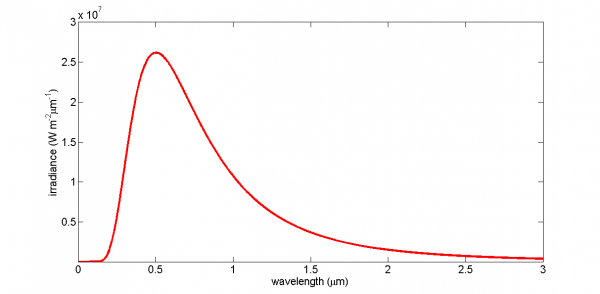
The Stefan–Boltzmann law (total) irradiance applies to an object that radiates according to the Planck distribution function spectral irradiance. If we look at the figure below, we see that the solar spectrum at the top of the atmosphere is similar to the Planck distribution function but does not follow it perfectly. However, the Planck distribution function with the same total irradiance as the sun has a temperature of 5777 K, as in the second figure.
Check Your Understanding
Clouds radiate. Assume two spherical clouds, one with a radius of 100 m and a temperature of 275 K and a second with a radius of 100 m and a temperature of 230 K. Assuming that they both radiate according to the Planck distribution function, calculate the emission for each cloud in W m–2 and in W. Which cloud is radiating more total energy and by how much?
ANSWER:
| Cloud T (K) | Cloud radius (m) | Fs (W m–2) | Fs x 4πRc2 (W) |
|---|---|---|---|
| 275 | 100 | 324 | 4.1 x 107 |
| 230 | 100 | 159 | 2.0 x 107 |
The warmer cloud is radiating about twice as much energy as the cooler cloud. These little clouds are radiating quite a lot of energy in all directions, but some of it is down toward Earth’s surface. If we make the simple assumption that half the radiation goes up and the other half goes down, the amount of energy radiated toward Earth’s surface per second is approximately 10 million W. If the clouds are not too far from the surface, this downward radiation could contribute a few hundred W m–2 of heating at Earth’s surface. Thus clouds can act like additional heat sources for Earth’s surface, keeping its temperature higher than it would be on a clear night. The image below is an infrared photograph of the sky above Ogden, Utah. Infrared radiation detected by the camera has been converted to temperature, with higher temperatures indicating more infrared emission.