Temperature and PV Performance Optimization

Effect of Temperature on the Module's Behavior

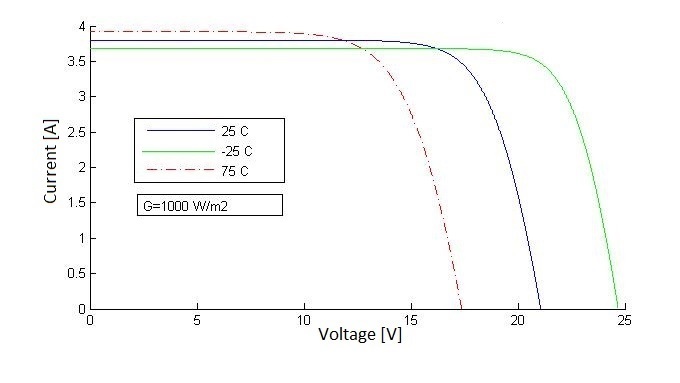
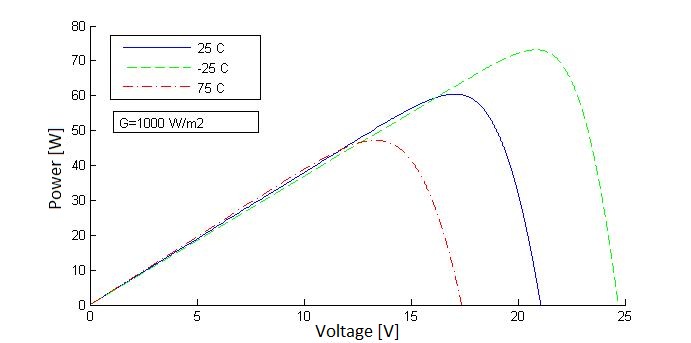
In regard to the temperature, when all parameters are constant, the higher the temperature, the lower the voltage. This is considered a power loss. On the other hand, if the temperature decreases with respect to the original conditions, the PV output shows an increase in voltage and power. Figure 2.9 is a graph showing the relationship between the PV module voltage and current at different solar temperature values. The figure illustrates that as temperature increases, the voltage, on the horizontal axis, decreases. Similarly, the relationship between the PV module voltage and power at different solar irradiance levels is shown in Figure 2.10. We can see that the power decreases as temperature increases, as illustrated by lower power peaks on the curves in Figure 2.10.

Figure 2.9: The effect of Temperature on I-V curve

Credit: Mohamed Amer Chaaban

Figure 2.10: the effect of Temperature on P-V curve

Credit: Mohamed Amer Chaaban

The drop in open-circuit voltage with temperature is mainly related to the increase in the leakage current of the photodiode “I0” in the dark with temperature. The “I0” strongly depends on the temperature.

The magnitude of voltage reduction varies inversely with Voc. 
This means that cells with higher Voc are less affected by the temperature than cells with lower Voc, as can be seen when a c-Si based solar cell, with a Voc of 0.65 V, is more affected than the a-Si with a Voc of 0.85 V.
 If the temperature of the PV module is increased by 10°C, how will the output be affected? The PV module manufacturers specify the temperature coefficients in the datasheets.

Temperature Coefficient

Temperature coefficient is defined as the rate of change of a parameter with respect to the change in temperature. It can be current, voltage, or power temperature coefficient. 
For example, the temperature coefficient of voltage is the rate of change of the voltage with temperature change. 
Similarly, temperature coefficient of power is the rate of change of the output power with temperature change.
 A typical datasheet of a commercial PV module specifies temperature coefficients for the power,
 Voc, and Isc under STC conditions. (Note: we will discuss the STC test conditions in the next topic).


Temperature coefficient are usually provided by the manufacturers and can be measured in terms of voltage change per degree ( V/°C) or as a percentage per degree change (%/°C).

Given these coefficients, how do we calculate the PV output with respect to the temperature change?

Effect of Temperature Change on Module's Parameters

In order for us to understand the numerical temperature effects on module, we need to define these two simple equations.


$$V=V_{STC}+V_{T-coeff}\times {(T_{Cell}-25)}^{o}C$$ $$P=P_{STC}+P_{T-coeff}\times {(T_{Cell}-25)}^{o}C$$

The terms Vstc and Pstc refer to the Voltage and Current taken at STC while the temperature coefficients of the voltage is represented by Vt-coeff and Pt-coeff, respectively.


It should be noted that the reference temperature taken for this calculation is the STC temperature (25°C
) as it appears on the equations.

Let's take an example.


If the maximum power output of a PV module under STC is 240 W, and the temperature coefficient of power is -2 W/°C, then the module's power output at a temperature of 30°C can be calculated as follows:

As you can see, the sign of the temperature coefficient determines if the parameter is increasing or decreasing with temperature.

In the previous example, when we said that the temperature was 30°C, did we mean the PV modules temperature or the ambient temperature? Are they equal? The simple answer is that module temperature or the cell temperature can be quite different from the ambient temperature.

Then, how do we estimate the module temperature based on the ambient temperature if we have to account for so many factors? 
Researchers developed a model provided in literature that gives a reasonable estimate of the module temperature as a function of the ambient temperature.
This model is sometimes called the NOCT model, due to the use of the Nominal Operating Cell Temperature.
 The NOCT is a parameter defined for a particular PV module. 
NOCT is the temperature attained by the PV cell under an irradiance of 800 W/m², with
a nominal wind speed of 1 m/s and an ambient temperature of 20°C.

$$T_{cell}=T_{ambient}+G\times \frac{(NOCT-{20}^{o}C)}{800\raisebox{1ex}{$W$}\!\left/ \!\raisebox{-1ex}{$m^2$}\right.}$$

Here, G is the irradiance at the instant when the ambient temperature is T_ambient.
The model gives the corresponding cell temperature as T_cell.
 As can be seen from this equation, the cell temperature is not only a function of the
 ambient temperature, but also of the irradiance.
 This makes things interesting, because if we consider the irradiance and temperature 
changes over a calendar year, we would see an effect of both irradiance and temperature 
across the seasons.

Temperature and Ideality Factor of PV Modules

So, how serious can temperature affect the performance of PV modules over the year?

 The difference between the expected PV yield with rated efficiency and the actual yield
 due to the temperature effect increases the module’s ideality factor, which is nothing but the ratio of the expected PV yield to the actually available, and taking into account the temperature effects.


When the ideality factor of a module is 80%, that means that the module has lost 20% of its annual energy yield due to temperature effects.
 If the module ideality factor is 100%, that means the module doesn’t change when temperature changes, and that is almost impossible.



Ideality Factor and PV module Type

As a result, we can see that the temperature effect on the module output is a function of the PV 
technology and the manufacturing process, which collectively decides the temperature 
coefficients of the PV module. The temperature effect is also a function of the ambient conditions.
 For the same technology, there could be a deviation in the temperature coefficients due to the manufacturing processes and other design modifications.

 The a-Si technology shows very low temperature coefficients due to their 
high open-circuit voltage.
This means it shows a better response under high temperatures.
 However, its efficiency is far lower compared to some of the best c-Si technologies.



According to IEA PV roadmap 2014, c-Si modules have the highest market share compared to other PV technologies such as a-Si. C-Si technologies dominate the global PV market with a share of 90%. In other words, every 9 of 10 PV installation is c-Si modules. If we look closer at the c-Si market, we can see that polycrystalline silicon is the most commonly used technology, according to an EPRI study, with a market share of 60%. This is due to the fact that it is the most efficient in terms of conversion efficiency and economics of scale that make it an affordable solution. 



Monocrystalline modules are more area-efficient, but are not the best economical solution. 
a-Si modules are more affordable, lighter, and sometimes even flexible, but give poorer yield and required more land area.



There is plenty of optimization to be done in order to choose an ideal PV module for your system. The optimum choice will depend on the location, ambient conditions, and of course, taking into account the budget of the client.