3.2: Reservoir Rock Properties

The reservoir rock properties that are of most interest to development geologists and reservoir engineers (amongst others) are Porosity, Compressibility, and Permeability. Porosity is a rock property that defines the fraction of the rock volume that is occupied by the pore volume. Compressibility is the rock property that governs the relative change in the pore volume when pressure is either increased or decreased. Finally, permeability is the rock property that is a measure of the ease (or difficulty) with which liquids or gases can flow through a porous medium.

Rock Porosity

As previously mentioned, porosity, ϕ, is the fraction of the Bulk Rock Volume, $v_b$ , that is occupied by the Pore Volume, $v_p$. Mathematically, it is defined as:

The bulk volume, V_b, can also be defined as the sum of the volumes of the two constituents of the rock, pore volume and Grain Volume, V_g. That is:

From these two expressions, we can develop several equivalent definitions for porosity:

Figure 3.03 (below) shows the porosities for three different idealized grain packings. In this figure, the rock grains are the spheres and the pore volume is the space between the spheres. Note that the porosities of these three systems are independent on the radii of the grains. In a real rock, the grains would be angular (if quartz grains in sandstones) and some of the void space might be filled with smaller grains, mineral cementation, and clays.

Figure 3.03: Porosities for Three Different Idealized Grain Packings

	$$\varphi =\frac{V_b-V_g}{V_b}=1-\frac{\pi }{6}=0.467$$ $$V_b={\left(2r\right)}^3$$ $$V_g=8\left[\frac{1}{8}\left(\frac{4}{3}\pi r^3\right)\right]=\frac{4}{3}\pi r^3$$
	$$\varphi =\frac{V_b-V_g}{V{}_b}=1-\frac{\pi r^3}{3\sqrt{3}{r}^3}=0.395$$ $$V_b=\left(2r\right)\left(2r\right)\left[r\sin (60)\right]=4\sqrt{3}{r}^3$$ $$V_g=\frac{4}{3}\pi r^3$$
	$$\varphi =\frac{V_b-V_g}{V{}_b}=1-\frac{4\pi r^3}{3\sqrt{3}{r}^3}=0.260$$ $$V_b=\left(2r\right)\left(2r\right)\left(h\right)=4\sqrt{2}{r}^3$$ $$h=\sqrt{4r^2-2r^2}=\sqrt{2}r$$ $$V_g=\frac{4}{3}\pi r^3$$

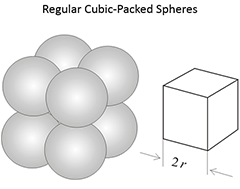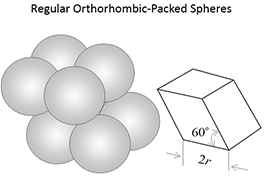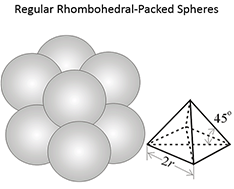At this point, we must distinguish between two types of porosity in rock: Total Porosity, ${\varphi }_t$, and Effective Porosity, ${\varphi }_e$. Real reservoir rock is comprised of connected pores and isolated pores. As the name implies, connected pores are pores which are connected to other pores and are capable of transmitting fluids. Isolated pores are pores, or groups of pores, which do not connect to other pores or form dead-end pathways. These isolated pores are incapable of transmitting fluids. Total porosity is defined as the total pore space (connected plus isolated pores) divided by the bulk volume, while effective porosity is the connected pore volume divided by the bulk volume.

Reservoir engineers are concerned with how fluids are stored and flow in the reservoir. Consequently, reservoir engineers are more concerned with effective porosity, ${\varphi }_e$

The porosity is of primary concern to geologists and reservoir engineers because it is a direct measurement of the ability of a reservoir rock to store fluids. There are two ways that oil and gas professionals can obtain measurements of porosity through laboratory measurement and through the use of Well Logs.