3.3.3: Natural Gas Properties

For natural gases we are also most interested in the Gas Formation Volume Factor, B_g, and the Gas Viscosity, μ_g, as these properties strongly influence gas storage (and accumulation) and gas flow. For most reservoir engineering calculations, the gas formation volume factor (and Gas Compressibility, c_g, and Gas Density, ρ_g) can be determined from the Real Gas Law, Equation 3.27:

$$pV=ZnRT$$

Where:

• p is the pressure of interest, psi
• V is the volume, ft³
• Z is the oil super-compressibility factor, dimensionless
• R is the gas constant, (psi ft³) / (lb-moles °R)
• T is temperature, °R (°R = °F + 460.67)

Gas Super-Compressibility Factor, Z

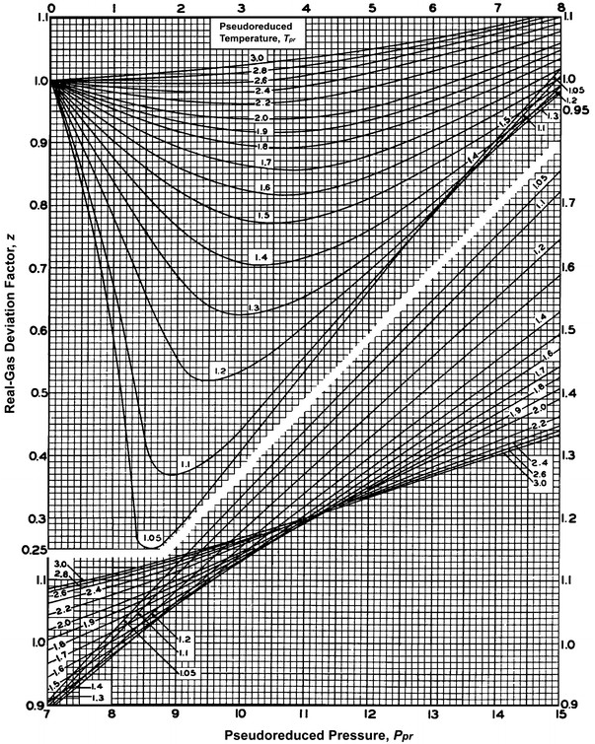
The gas supercompresibility factor, Z (or Z-Factor, or Real Gas Deviation Factor), is a function of pressure and temperature that corrects the Ideal Gas Law for high pressure and high temperature conditions. In the oil and gas industry, the z-factor correlation for hydrocarbon gases that is universally accepted in the Standing-Katz Correlation^[12]. This correlation is shown graphically in Figure 3.12.

As illustrated in Figure 3.12 The Standing-Katz Correlation correlates the z-factor to the Pseudo-Reduced Pressure, p_pr, and Pseudo-Reduced Temperature, T_pr. The pseudo-reduced properties are defined by:

and

Where:

• p is the pressure of interest, psi
• p_pc is the pseudo-critical pressure, psi
• T is temperature of interest, °R
• T_pc is pseudo-critical temperature, °R

All of these properties are called pseudo-properties because the pseudo-critical pressure and pseudo-critical temperature are not the true, measured critical properties, but are calculated properties:

and

with

Where:

• p_pc is the pseudo-critical pressure, psi
• T_pc is the pseudo-critical temperature, °R
• ϒ_g is the gas gravity (MW_g/MW_air), dimensionless
• MW_g is the molecular weight of the gas, lb/lb-mole
• MW_air is the molecular weight of air, lb/lb-mole (28.97 lb/lb-mole)

In cases where significant concentrations of inorganic impurities, CO₂ and H₂S are present, then corrections to Equation 3.61 and Equation 3.61 are required:

and

with

Where:

• p_{pc corrected} is the corrected pseudo-critical pressure, psi
• p_{pc Eq. 3.61} is the pseudo-critical pressure from Equation 3.61, psi
• T_{pc corrected} is the corrected pseudo-critical temperature, °R
• T_{pc Eq. 3.60} is the corrected pseudo-critical from Equation 3.60, °R
• ϵ_correction is the correction for CO₂ and H₂S, °R
• y_CO2 is the mole fraction of CO₂ in the gas phase, fraction
• y_H2S is the mole fraction of H₂S in the gas phase, fraction

The Standing-Katz^[12] correlation has also been mathematically curve fit^[13]. The equation for z-factor then becomes:

with

It should be noted that the solution of this equation for the z-factor requires an iteration procedure. This is because the z-factor appears both on the left-hand side of Equation 3.66 and the right-hand side of the equation through the pseudo-reduced density, ρ_pr. Typically, this is solved with a Newton-Raphson iteration procedure which is beyond the scope of this class. For our purposes, if supercompressibility factors are required, we can simply read the chart to obtain them.

Real Gas Formation Volume Factor, B_g

The Formation Volume Factor, B_g, of a real gas, like its oil phase analog, is used to convert one standard cubic foot, SCF, of gas at reference conditions to its volume at reservoir conditions. For natural gases, in the U.S. domestic oil and gas industry, we use the standard conditions of p_SC = 14.7 psi and 60 °F. The gas formation volume factor for a real gas can be calculated directly from the Real Gas Law once we have an estimate of the super-compressibility factor. If we assume one lb-mole of natural gas, then the volume that it would occupy at standard conditions would be (assuming Z_SC = 1.0 at standard conditions – a very good assumption):

$$V_{SC}=\frac{Z_{SC}nR{T}_{SC}}{p_{SC}}=\frac{nR{T}_{SC}}{p_{SC}}\mathrm{in}f{t}^3;with{Z}_{SC}=1.0$$

At reservoir conditions, that same lb-mole would occupy a volume of:

$$V_r=\frac{ZnR{T}_r}{p_r}inf{t}^3$$

Now, the gas phase formation volume factor we can define as:

There are times when we would like to consider the volume of gas in reservoir barrels, bbl. This is because we have used reservoir barrels as the units for the liquid (oil and water) volumes, and we would like to determine the volume occupied by the gas and liquids combined. We can convert the units of Equation 3.68a by applying the unit conversion constant of 1 bbl = 5.615 ft³:

Where:

• B_g is the gas formation volume factor, ft³/SCF (Equation 3.68a) or bbl/SCF (Equation 3.68b)
• Z is the supercompressibility factor at reservoir conditions, p_r and T_r, dimensionless
• T_r is the reservoir temperature, °R
• T_SC is the reference (standard) temperature (520 °R in U.S. domestic industry), °R
• p_r is the reservoir pressure, psi
• p_SC is the reference (standard) pressure (14.7 psi in the U.S. domestic industry), psi

Real Gas Compressibility, c_g

The isothermal compressibility of a real gas can also be determined directly from the Real Gas Law. Starting with the definition of isothermal compressibility:

Substituting the Real Gas Law, Equation 3.27, into Equation 3.69:

or

The derivative, $\frac{dZ}{dp}$ , can be calculated by differentiating Equation 3.66 and Equation 3.67 with respect to pressure.

Real Gas Density, ρ_g

The density of a real gas can also be determined directly from the Real Gas Law. Starting with the Real Gas Law:

$$pV=ZnRT$$

Now the number of moles is equal to a mass divided by the molecular weight, n = m / MWg. Substituting into the Real Gas Law:

$$pV=\frac{ZmRT}{M{W}_g}$$

Now from the definition of gas density and the substitution of the Real Gas Law:

Where:

• ρ_g is the gas density, lb/ft³
• p is the pressure of interest, psi
• MW_g is the molecular weight of the gas, lb/lb-mole
• Z is the supercompressibility factor at reservoir conditions, p_r and T_r, dimensionless
• R is the Gas Constant, 10.73 ft³ psi / °R lb-mole
• T is the temperature of interest, °R

Real Gas Specific Gravity, γ_g

The specific gravity of a real gas can also be determined directly from the Real Gas Law. For gases, the specific gravity is defined as the ratio of the density of the gas to the density of air at standard conditions. Dividing Equation 3.71 written for a gas by Equation 3.71 written for air at standard conditions (Z = 1.0) results in:

Now, the molecular weight of gas is 28.87 lb/lb-mole:

Real Gas Viscosity, μg.

The viscosity of natural gases can be determined by the correlation of Lee, Gonzalez, and Eakin^[14]:

with

Where:

• μ_g is the gas viscosity, cp
• K, X, and Y are correlation coefficients
• ρ_g is the gas density at the pressure and temperature of interest, gm/cc
  $\left[{\rho }_g\left(gm/cc\right)=1.4935\times {10}^{-3}\frac{M{W}_{g}p}{zT}\right]$
• MW_g is the molecular weight of the gas, lb/lb-mole
• T is the temperature of interest, °R

---

^[12] Standing, M.B. and Katz, D.L.: "Density of Natural Gases," Trans., AIME (1942) 146, 140-49.

^[13] Dranchuk, P.M. and Abou-Kassem, J.H.: "Calculations of z-Factors for Natural Gases Using Equations of State," J. Cdn. Pet. Tech. (July-Sept. 1975) 34-36.

^[14] Lee, A.L., Gonzalez, M.H., and Eakin, B.E.: "The Viscosity of Natural Gases," JPT (Aug. 1966) 997-1000; Trans., AIME (1966) 234.