Additional reading from www.astronomynotes.com
There is an old, simple question that can help us to understand a fundamental property of the universe. The question is usually called Olbers' Paradox, (after German astronomer Heinrich W. Olbers), and it can be stated pretty simply:
Why is the night sky dark?
The reason that this question is so important is because its answer can tell us about the distribution of stars and galaxies in the universe.
Consider the possibility that the universe is infinite and that it is filled with luminous objects (stars and the galaxies that contain them). If this is true, then every sight line from the Earth will eventually intersect a bright object. This means that if the universe is infinite and contains an infinite number of bright objects, the night sky will be bright! Since the night sky is dark, this tells us that one of our assumptions about the universe is incorrect. I made a pretty basic illustration of this, shown below:
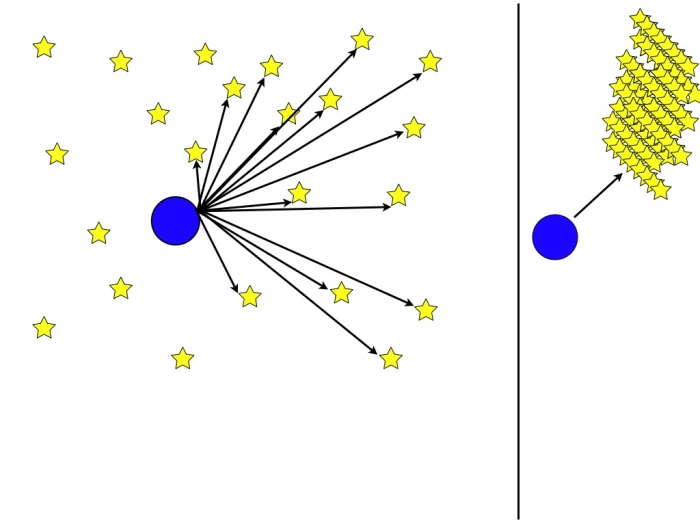
In the left panel, what is represented is the Earth in a 3D universe with stars arranged randomly around the planet. From one particular vantage point, you can draw sight lines from Earth to every star within your field of view. If the Universe is infinite and filled with stars all at different distances from Earth, then every single sight line should land on a star. So, in the right panel, this is illustrated; you should see in projection a night sky filled with stars. An analogy is standing in the middle of a large forest -- every direction you look, your line of sight should end on a tree, as shown in the image below.
Let's briefly consider the mathematics of this situation. You know from many discussions previously that every object appears fainter the more distant it is from Earth, and the brightness of that object drops off as 1/d2, or an object twice as far away is 1/4th as bright. If we picture spherical shells surrounding the Earth, though, the number of stars covering the surface area of one particular shell will increase by exactly the same amount as the brightness of the stars on that shell decreased, so the surface brightness, that is, the brightness per unit area on the sky, will be the same for every shell. There is an excellent public domain visualization of this phenomenon in the Wikimedia Commons; it shows the sky randomly filling with more distant, and therefore fainter objects, but since the number of faint objects is so large, the picture of the sky eventually fills with a light of uniform brightness.
This is the source of the paradox. If the universe is infinite and filled with stars, the surface brightness of the night sky should be the same as the Sun's, so the night sky should be as bright as the daytime sky. Even though this is obvious by simply looking at the sky, when you review the image of the Hubble Ultra Deep Field, there is clearly dark sky visible between every galaxy, providing further evidence that every sight line does not end on a luminous object.
Based on what you have learned so far, you may have a few questions.
- Does it matter that we considered stars and not galaxies? No, because the same logic holds for galaxies. If every one of your sight lines ended on a galaxy, the night sky would be bright.
- Is there enough dust in the Universe to block our sight lines to some stars or galaxies? Yes, but if the Universe was infinite and with an infinite number of stars and galaxies, the light from those objects would heat up the dust causing it to glow brightly enough to light up the night sky.
The solution to the paradox (why is the night sky dark?) could be due to several different possibilities:
- The universe is finite, that is, it ends at some point.
- The stars run out at large distances.
- There hasn't been enough time for the light to reach us from the most distant stars.
We will find out shortly that we can actually estimate the age of our universe. Because the universe is not infinitely old, the answer is number 3 listed above. Since light takes time to reach us, we can see only those objects that are near enough to us that their light has reached us. Curiously enough, the first published solution to Olbers' Paradox is attributed to Edgar Allan Poe. In his essay Eureka, Poe says:
Were the succession of stars endless, then the background of the sky would present us a uniform luminosity, like that displayed by the Galaxy - since there could be absolutely no point, in all that background, at which would not exist a star. The only mode, therefore, in which, under such a state of affairs, we could comprehend the voids which our telescopes find in innumerable directions, would be by supposing the distance of the invisible background so immense that no ray from it has yet been able to reach us at all.
While we know the solution today for Olber's Paradox, it took until well into the 20th century for us to truly understand the nature of the Universe well enough to explain the answer to this question. In the rest of this lesson, you will find out how we came to understand the Universe and prove to ourselves the reason the night sky is dark.
Want to learn more?
The Wikipedia Page on Olbers' Paradox has a bit more background information on the history of this question if you are interested in finding out more.

