The Implications of Hubble's Law: An Expanding Universe

Additional reading from www.astronomynotes.com

• Universe is Uniform on Large Scales: No Center to the Expansion in 3D Space

Like Kepler's Laws, Hubble's Law is an empirical law. Hubble discovered a relationship between two measurable properties of galaxies: their velocities and their distances. Given this relationship, though, it naturally leads to several questions. These questions are:

• What is the cause of this relationship?
• Why should more distant galaxies have larger velocities?

On the previous page, we attributed the velocities of galaxies and the relationship between their velocities and distances to an explosion. Because all of the pieces of debris from an explosion originated at the same spot, the more distant ones must be moving faster to have traveled the farthest in the same amount of time. This is an acceptable analogy, but it is not perfect. It does, however, help us understand that the universe must be expanding. Our best interpretation of the relationship discovered by Hubble is that it implies that the space between galaxies is expanding.

Let's study this idea of an expanding Universe in a bit more detail. If all objects are moving outward at a constant speed, the boundaries defined by the outermost objects must be continuously growing. To be more precise about the expansion of the universe, we again resort to analogies. The first is this: picture dots on a very long rubber band. The dots are supposed to represent galaxies. If you pull on the rubber band, the distance between the dots will grow. If the initial distance between each dot is 1 cm (Dot B is 1 cm away from Dot A, Dot C is 2 cm away, and Dot D is 3 cm away) and you pull on the rubber band so that the dots are now 2 cm apart, then from Dot A, Dot B will be 2 cm away, Dot C will be 4 cm away, and Dot D will be 6 cm away. Dot C will have moved twice as far from Dot A in the same amount of time as Dot B did, and Dot D will have moved three times as far from Dot A in the same amount of time as Dot B did. Therefore, from Dot A's point of view, the more distant dots will appear to have moved faster than the closer dots (remember, the velocity of an object is the distance traveled divided by the time it takes to go that distance).  If we were to repeat the previous experiment, but measure the distances between the dots from Dot B's point of view, we would find that Dot B would draw the same conclusion as Dot A. That is, all the dots would appear to be moving away from Dot B, and the farther dots would appear to move faster.

Rubber band / dot analogy of the expanding universe.  In an example initial state, galaxies appear as dots along a rubber band.  The blue and yellow dots are equidistant from the point of origin, as are the white and pink dots, albeit in opposite directions.  The orange dot is between the white and blue dot, and closer to the point of origin.  The green dot is between the yellow and pink dot, and farther from the point of origin.

Credit: Penn State Department of Astronomy & Astrophysics

Rubber band / dot analogy of the expanding universe.  The universe's expansion, when doubled in size, causes all th dots to appear twice as far as they once were, from the perspective of the point of origin.  This means that the white and pink dots have appeared to move much farther from the point of origin compared to the blue and yellow dots, in opposite directions from the point of origin.  However, taking the perspective of the pink dot, the green dot has not appeared to move much compared to the white dot.

Credit: Penn State Department of Astronomy & Astrophysics

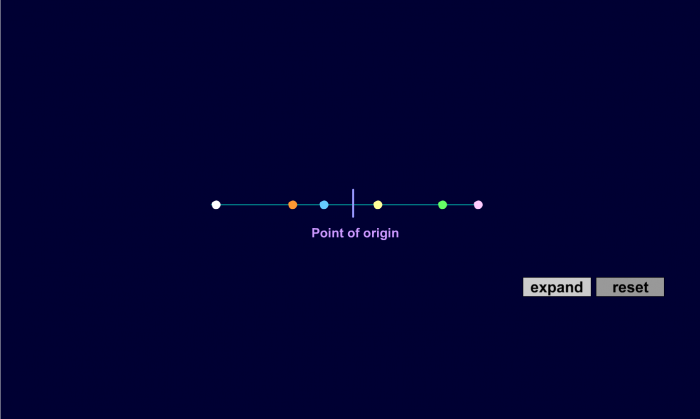
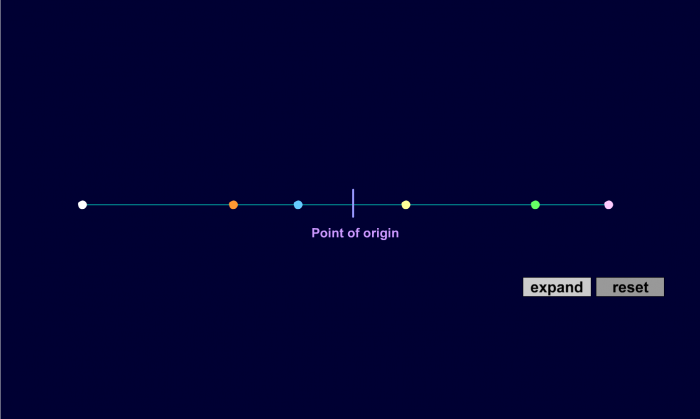
The analogy in the figure above allows us to draw several conclusions about the universe.

1. The galaxies are not really moving through space away from each other. Instead, what is happening is the space between them is expanding (just like the rubber band expanded, separating the dots fixed to it from each other). As the universe expands, the galaxies get farther from each other, and the apparent velocity will appear to be larger for the more distant galaxies.
2. The Earth and the Milky Way are not special in seeing that all galaxies appear to be moving away from us. If we were on a different galaxy, we would also see all the other galaxies appear to be moving away from us because of this expansion.

The next two analogies are similar to the rubber band / dot analogy, but we are going to think in more dimensions, since we know that the galaxies are not restricted to be found along a one dimensional line. Instead of a line, picture the dough for raisin bread. Inside the dough, all of the raisins are separated from each other. As the dough rises during baking, all of the raisins will move farther away from each other. Let's say that the size of the dough doubles. The distance between all of the raisins will double, and just like the dots on the rubber band, the more distant raisins will appear to have moved faster. This is represented well in the animated image from the NASA WMAP mission included below.

Figure 10.6: Animated image showing the rising of a loaf of raisin bread dough. This animation contains the same idea as in Figure 10.5, but expanded to three spatial dimensions instead of one.  The raisins in the dough are like the dots on the rubber band or galaxies in the Universe.  As the dough expands, the separation between the raisins increases, just like the separation between galaxies in our Universe.

Credit: NASA / WMAP

Both of the two analogies (rubber band and raisin bread) should allow you to picture that every galaxy (or dot or raisin) will see all other galaxies moving away if the space between them is expanding. We use one more analogy to try to explain the mathematics of the expansion of the universe and to answer another common question that arises in cosmology:

• Why can't we observe the center of the expansion?

Picture a universe that consists only of the surface of a balloon. All of the galaxies and the stars in the galaxies are fixed onto the surface of the balloon. There is no way for the observers to perceive the region inside the balloon or the region outside the balloon, they are (and light is) constrained to travel only along the surface. In this analogy, as the balloon inflates, the galaxies on the surface of the balloon will move farther away from each other. Just like with the rubber band and raisin analogies, if you measure the distance between the galaxies before and after the inflation of the balloon, you will be able to show that the more distant galaxies will appear to move faster, just like Hubble's Law in our universe (and like the rubber band and raisin loaf experiments). Again, every galaxy will observe the same effect, and no one galaxy is in a special location. If you ask where the center of the expansion is, it is inside the balloon. This means that no location on the surface of the balloon (the universe according to the residents on the surface of the balloon) can be identified as the "center" of the universe.

We use this analogy to answer the question:

• Where is the center of our universe?

The idea is that we live in a universe with three spatial dimensions that we can perceive, but that there exist "extra" dimensions (maybe one, maybe more than one) that contain the center of the expansion. Just like the two-dimensional beings that inhabit the surface of the balloon universe, we cannot observe the center of our universe. We can tell that it is expanding, but we cannot identify a location in our 3D space that is the center of the expansion.

Until this point, we have been describing the redshift of light as a Doppler shift. However, now that we understand the Universe to be expanding, we need to revise this description. The way we understand the cosmological redshift of galaxies is as follows. Picture a photon emitted by a distant galaxy towards the Earth. That photon has a specific wavelength. However, during the trip between the distant galaxy and Earth, the space between that galaxy and Earth has expanded. The expansion of space causes the wavelength of the photon to stretch, so when it arrives at Earth, it has a longer wavelength than when it left. Mathematically, this behaves exactly as if the photon was Doppler shifted. So, we interpret the galaxies as moving through space away from us. However, the proper interpretation is that the galaxies are at specific positions in space, and the space between them is expanding. An animation illustrating the cosmological redshift using the balloon analogy for the expansion of space is below.

Does this mean that the Solar System is expanding? What about the Milky Way? Will Pluto get farther and farther from the Sun as the Universe expands? The answer is no, and it is a bit difficult to understand exactly why. Consider again a stable Main Sequence star. We discussed how in order for a star to avoid collapse, the outward force of the radiation pressure created by the nuclear fusion in the core balanced the inward pull of gravity. We can consider all objects and systems of objects in the universe subject to the same kind of balance of forces. The expansion of the universe can be thought of as a global force that is pulling on all objects. However, it is only strong on very large scales. At the scale of a galaxy, the gravitational force binding a galaxy together is much stronger than the "expansion force," so the galaxy does not expand. At the scale of the Solar System, the imbalance is even larger, so the gravitational binding of the Solar System easily overwhelms the "expansion force," keeping Pluto's orbital separation from the Sun the same over time.