Additional reading from www.astronomynotes.com
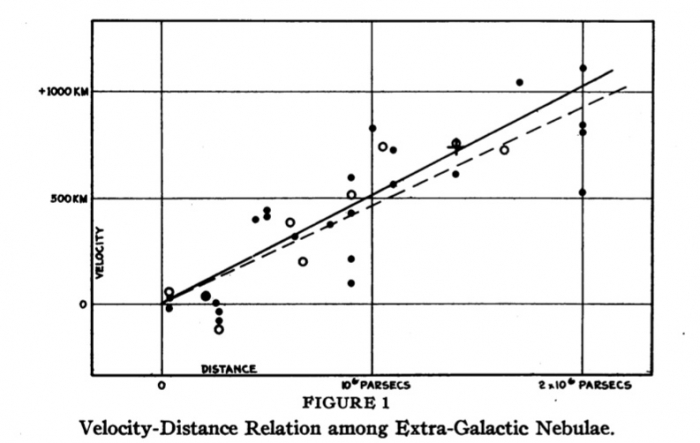
During his work studying galaxies, Hubble used Cepheid variable stars to measure the distances to a sample of galaxies. Even before the Shapley/Curtis debate and the discovery that spiral nebulae are external galaxies, observations had shown that the vast majority of galaxies had spectral lines redshifted from the laboratory values. If you recall from our work on the Doppler effect, a redshift in a spectral line indicates that the object is moving away from us. In a publication by Hubble in 1929, he showed that if you plot the distance to a galaxy (measured from Cepheid variables) and the velocity of the galaxy (measured by the shift in the spectral lines), the two quantities are directly correlated! See the reproduction of his plot below.
Want to learn more?
Read Hubble's original articles! The astronomical community maintains an excellent resource meant primarily for practicing astronomers. It is the SAO/NASA Astrophysics Data System, and you can use it to search the astronomical literature. For example, if you want to find information on every article I have ever published, you can go there and stick my name in the author field. However, for a much more interesting search, you can go there and put in "Hubble, E" in the author field, and it will bring up the listing of Hubble's published works, including the paper in which he published the plot above.
Interpreting these diagrams
On the y-axis, you plot the velocity of the galaxy obtained from the spectrum. On the x-axis, you plot the distance to that galaxy, in this case obtained from Cepheids. If these two quantities (distance and velocity) had nothing to do with each other, then the diagram would look like what we call a "scatter plot." That is, it would appear as a bunch of points randomly placed in different locations. However, it is somewhat apparent in this case that you can draw a straight line through the points. What this means is that as the distance gets bigger, so does the velocity. In algebra class, you learned that the equation for a line that passes through the point (0,0) is:
where y = the quantity plotted on the y-axis (velocity), x = the quantity plotted on the x-axis (distance), and m is the slope of the line. For the specific case of this relationship, we usually write the equation this way:
H0 is called the Hubble constant. It is the slope of the line that relates the distance of a galaxy to its velocity. If you know H0 and if you can calculate the velocity, v, from the spectrum, then you can use this equation to calculate the distance, d, to that galaxy. Let's quickly review how we measure velocities for objects that are receding from us. The equation that you saw in Lesson 4 for the Doppler shift was:
Where Δλ is the difference between the measured wavelength for a line in the spectrum of an object and the wavelength for that same line observed in the spectrum of an object at rest. The other term on the left hand side, λ0, is the wavelength of that line in the spectrum of an object at rest. For objects at large distances from Earth where the distance is determined using Hubble's Law, we do not often refer to their recession velocities (e.g., "that galaxy has a velocity of 14,000 km/sec away from us") or their distances in Mpc (e.g., "that galaxy is 247 Mpc from us"), instead, we simply refer to the object's redshift, z. The definition of z is that it is the left hand side of the Doppler shift equation:
For example, if you observe a galaxy with an H-alpha line at 680 nm, and you know the rest wavelength for that line is 656.3 nm, then its redshift is:
Hubble's law, which says simply that a galaxy's velocity (or as is sometimes plotted, its redshift) is directly proportional to its distance, also tells us something important about the state of the universe. If the universe is static and unchanging, there should be no correlation between distance and velocity. However, if the universe is expanding, we expect a correlation between distance and velocity. The usual analogy used here is that of an explosion – the fragments of shrapnel produced are moving with a range of velocities, and the most distant objects from the source of the explosion have the largest velocities. Astronomers believe that Hubble's law is a direct consequence of the ongoing expansion of the universe and that the evidence suggests that the universe began in an explosion, which we call the Big Bang.
There are a couple of important caveats that apply to Hubble's Law. They are:
- Hubble's Law only works for distant galaxies. For nearby galaxies (in the Local Group), stars inside the Milky Way, and for objects in our Solar System, the relationship between distance and velocity does not hold. The reason for the discrepancy for nearby galaxies is the "peculiar velocity" of the galaxy, that is, its real velocity through space that is unrelated to the expansion. For distant galaxies, their peculiar velocities are small enough that they still lie on or near the line for Hubble's Law. For nearby galaxies, though, their peculiar velocity is larger than their velocity from the expansion, so their peculiar velocity dominates their total velocity, causing them to lie far from the line relating velocity to distance. For example, the galaxy M31 does not even show a redshift; it is blueshifted, showing that its peculiar velocity is pointed towards us, rather than away from us.
- Recall the concept of the "lookback time" for an object. For objects at very large distances from us, it is very common to see their distances referred to not in units like parsecs or light years, but in units of time. For example, astronomers will say, "The light from this galaxy was emitted when the universe was 10% of its present age, over 12 billion years ago." We base these descriptions on the redshift of the galaxy and the lookback time.
You can consider Hubble's Law to be the final rung in the distance ladder. If you know Hubble's constant accurately, then you can calculate the distance to any galaxy in the Universe simply by measuring its velocity (which is reasonably easy to do for any galaxy for which you can observe its spectrum). To calibrate Hubble's constant, though, you need to be able to plot the distances for a number of galaxies as obtained using other methods. While that may seem like an easy statement to make, it was an incredibly difficult task to accomplish. For decades, astronomers have argued over the precise value of Hubble's constant. This measurement was, in fact, one of the major reasons for building and launching the Hubble Space Telescope. It spent years observing Cepheid variables in distant galaxies in order to measure Hubble's constant as precisely as possible. The results were reported in 1999. See "Hubble Completes Eight-Year Effort to Measure Expanding Universe."
Note that in Hubble's diagram, above, he has data on galaxies out to 2 Mpc (that is, 2,000,000 parsecs). The diagram produced by the Hubble Key Project team used data on galaxies out to about 23 Mpc.