4.1 Photovoltaic effect

The word "photovoltaic" immediately indicates the connection between light (phot- greek) and electricity (volt, unit for electric potential). The key property of a photovoltaic material is to convert light energy to electric current. This conversion takes place due to the photovoltaic effect - a physical phenomenon in a semiconductor, which we are going to discuss next.

Semiconductors are a special class of materials, whose conductance is not permanent, but rather depends on the energy available to activate electrons in the crystal lattice. Crystalline silicon is a semiconductor material widely used in photovoltaics. It becomes conductive when the energy of the photons absorbed by the crystal surface is sufficient to raise the electron state from the valence band to the conduction band. This required amount of energy to excite an electron is defined as band gap. Band gap is an intrinsic property of semiconductors and eventually has a direct influence on the photovoltaic cell voltage. The following schematic (Figure 4.1) provides a demonstration of the band gap concept.

Demonstration of the band gap concept. See surrounding text for details.

Figure 4.1. Schematic illustration of the band gaps in various materials. The vertical axis is the electron energy, and E_F is the position of the Fermi level.

Credit: Band Filling Diagram.svg from Wikimedia.org

In this picture, we can visualize the difference between different classes of materials: conductors (metals), semiconductors, and insulators. The valence and conduction bands in a metal overlap, so it does not take any significant energy to free the electrons. They are available for conduction as soon as the potential gradient is provided. In insulators, the gap between the valence and conduction bands is very large, so it requires so much energy to free the electrons that it can damage the material itself. For semiconductors, the situation is somewhere in between. The band gap is big enough to prevent spontaneous conduction and to provide separation of charges, and small enough to be matched by photon energy.

The band gap energies of several different materials are listed in Table 4.1 below. Some of those materials are more suitable for photovoltaic applications than others. How suitable the materials are for photovoltaic applications would be determined by how close the photon energy is to the band gap of the material, and if the energy of photon is sufficient to cover the band gap.

Table 4.1. Band gaps of different materials [source: Wikipedia: Band Gap from Wikipedia.org]
Material		Band Gap (eV)
Si	Silicon	1.11
Ge	Germanium	0.67
CdTe	Cadmium telluride	1.5
Cu₂O	Copper oxide	2.1
Cu₃N	Copper nitride	1.75
GaP	Gallium phosphide	2.26
GaAs	Gallium arsenide	1.43
PbS	Lead sulfide	0.37
Si₃N₄	Silicon nitride	5
C	Diamond	5.5
SiO₂	Silica	9

For example, if we have a photon with energy of 2 eV hitting silicon surface, 1.1 eV of that energy will be used to move an electron to the conduction band; the rest of the energy (0.9 eV) will be dissipated as heat. However, if a material with a greater band gap is used, for instance copper oxide, 2 eV is not enough to free the electron. We would need a higher energy photon there.

By the way, you may remember from physics that photon energy is dependent on the wavelength of light. The shorter the wavelength (λ), the higher the frequency of the light (ν), and the more energy it brings:

$E = h ν = h (C / λ)$ (where h is the Plank constant, and C is the speed of light)

For instance, for the red side of the visible light spectrum, $λ \approx 700 n m$ , so we can find:

$E = 4.136 × 10^{- 15} e V. s × (3 × 10^{8} m / s / (700 × 10^{- 9}) m) = 1.77 e V$

At the same time, for the violet side of the visible spectrum, $λ ≈ 400 n m$ , and:

$E = 4.136 × 10^{- 15} e V. s × (3 × 10^{8} m / s / (400 × 10^{- 9}) m) = 3.10 e V$

Obviously, the photons associated with high frequency radiation (violet, UV) deliver more energy and can be used with larger band gap materials.

Check this out

Photon energy calculator from the PVEducation website.

Check the numbers given in the above example. You may also want to see what light wavelengths would be suitable for the materials listed in Table 4.1.

Based on these reflections, we see that low band gap materials (such as germanium), can be used to capture low energy photons (like those in the red and IR parts of the spectrum), and high band gap materials (e.g. copper nitride or gallium phosphide) can be used for using high energy photons. Combination of different materials in one system allows for more efficient use of available radiation. At the same time, if the band gap of the PV material is too small compared to the incident photon energy, a significant amount of energy will be converted to heat, which is not a good thing for PV cell itself. No matter how much higher the photon energy is compared to the band gap, only one electron can be freed by one photon. This is the reason for the limited efficiency of the photovoltaic cells.

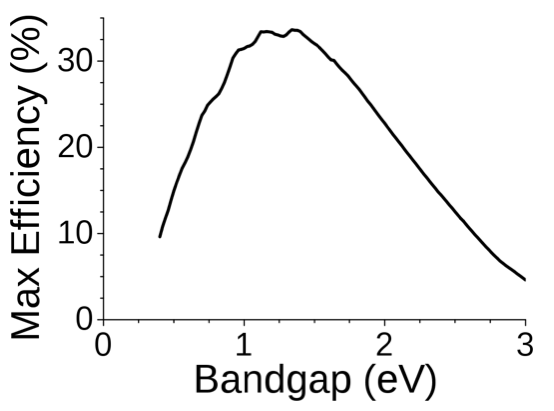
The data in Figure 4.2 show how the maximum efficiency of a solar cell depends on the band gap. If the band gap is too high, most photons will not cause photovoltaic effect; if it is too low, most photons will have more energy than necessary to excite electrons across the band gap, and the rest of energy will be wasted. The semiconductors commonly used in commercial solar cells have band gaps near the peak of this curve, for example silicon (1.1eV) or CdTe (1.5eV). The Shockley–Queisser limit (33.7%) defined at the peak of the curve has been exceeded experimentally by combining materials with different band gap energies into tandem solar cells.

The data show how the maximum efficiency of a solar cell depends on the band gap. (See surrounding text.)

Figure 4.2. The prediction of the solar cell maximum efficiency as a function of material band gap by the Shockley–Queisser limit.

Credit: ShockleyQueisserFullCurve.svg from Wikipedia.org

Next, please refer to the following reading to learn more about the background of the photovoltaic effect:

Reading Assignment

Brownson, J.R.S., Solar Energy Conversion Systems, Chapter 14: Systems Logic of Devices: Optoelectronics, pp. 349-356. (See E-Reserves via the Library Resources tab.)

Based on the above reading, we can summarize that the photovoltaic effect essentially includes three main steps:

Absorption of light (photons)
Generation of charge carriers
Separation of charge carriers between electrical contacts

When all these steps occur, the system is able to generate electric current (flow of charge carriers), which can do work.

Answer the following questions for self-check:

Check Your Understanding - Question 1 (Multiple Choice)

Check Your Understanding - Question 2 (Essay)

Calculate the photon energy corresponding to the radiation wave length of 500 nm.

Check Your Understanding - Question 3 (Essay)

List three main stages of the photovoltaic effect:

4.1 Photovoltaic effect